Cardinality of a Set - Definition, Examples, Quiz, FAQ, Trivia
Learn about sets and how to count their elements with fun examples and activities
What is Cardinality?

Cardinality is a math word that tells us how many things are in a group or set. It's just a fancy way to say "the number of elements" in a collection.
Think of a set as a basket where you put things. The cardinality is how many items are in your basket. For example:
This set has three fruits, so its cardinality is 3. We write this as |A| = 3 or n(A) = 3, where A is the name of our set.
Key Concept
Cardinality = Number of unique elements in a set
How to Find Cardinality of a Set
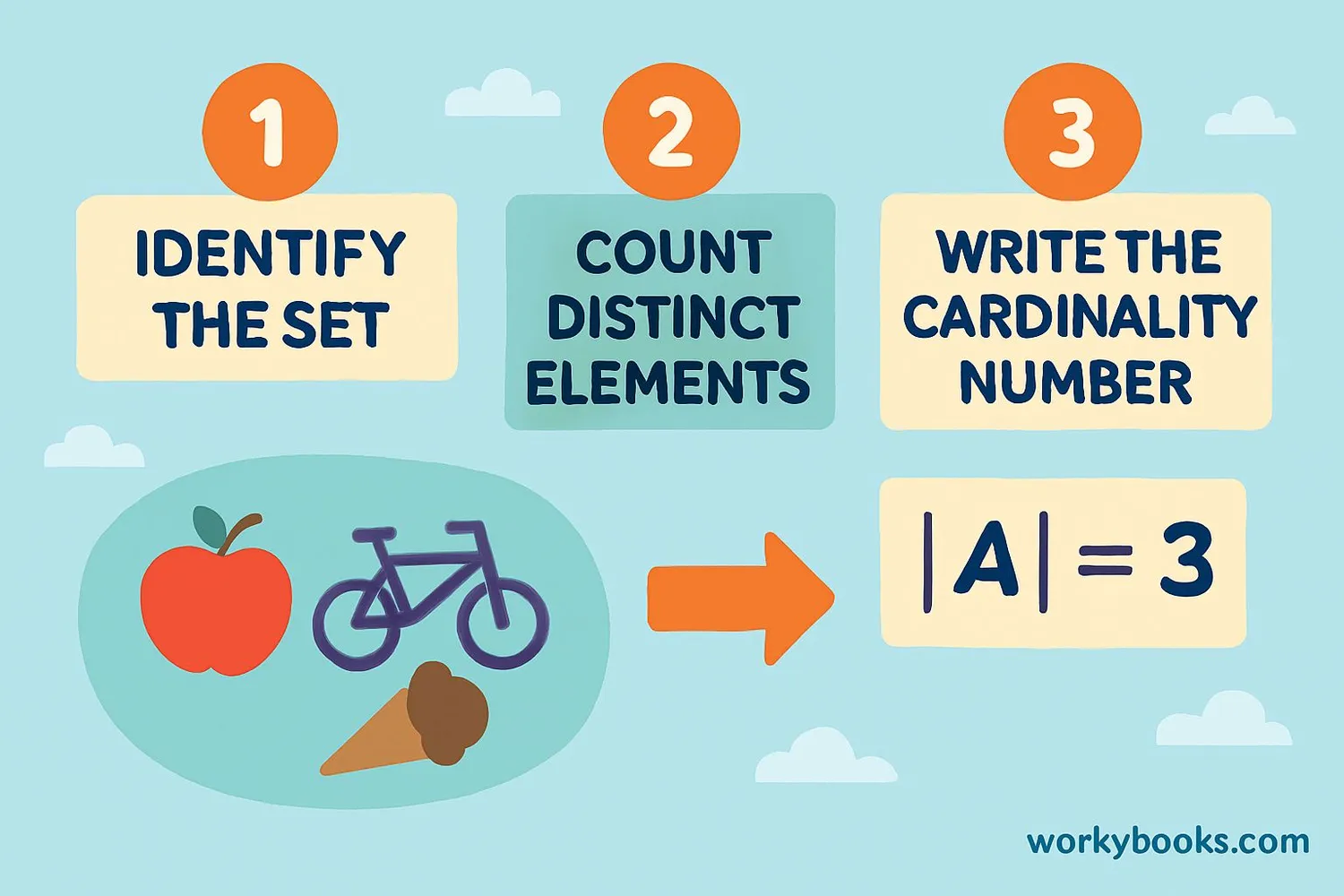
Finding the cardinality of a set is like counting how many different toys you have in your toy box. Here's how to do it:
Step 1: Identify all the elements in the set. Remember, sets only count each item once - no duplicates!
Step 2: Count each distinct element. You can use your fingers, draw dots, or make tally marks.
Step 3: The total number is the cardinality.
Important Rule
Sets only contain unique elements. If you have duplicates, they don't count extra!
Set B = {dog, cat, dog, bird}
Even though "dog" appears twice, we only count it once. So the elements are: dog, cat, bird. Cardinality = 3.
Remember
The empty set {} has no elements, so its cardinality is 0. We write this as |∅| = 0.
Examples of Cardinality
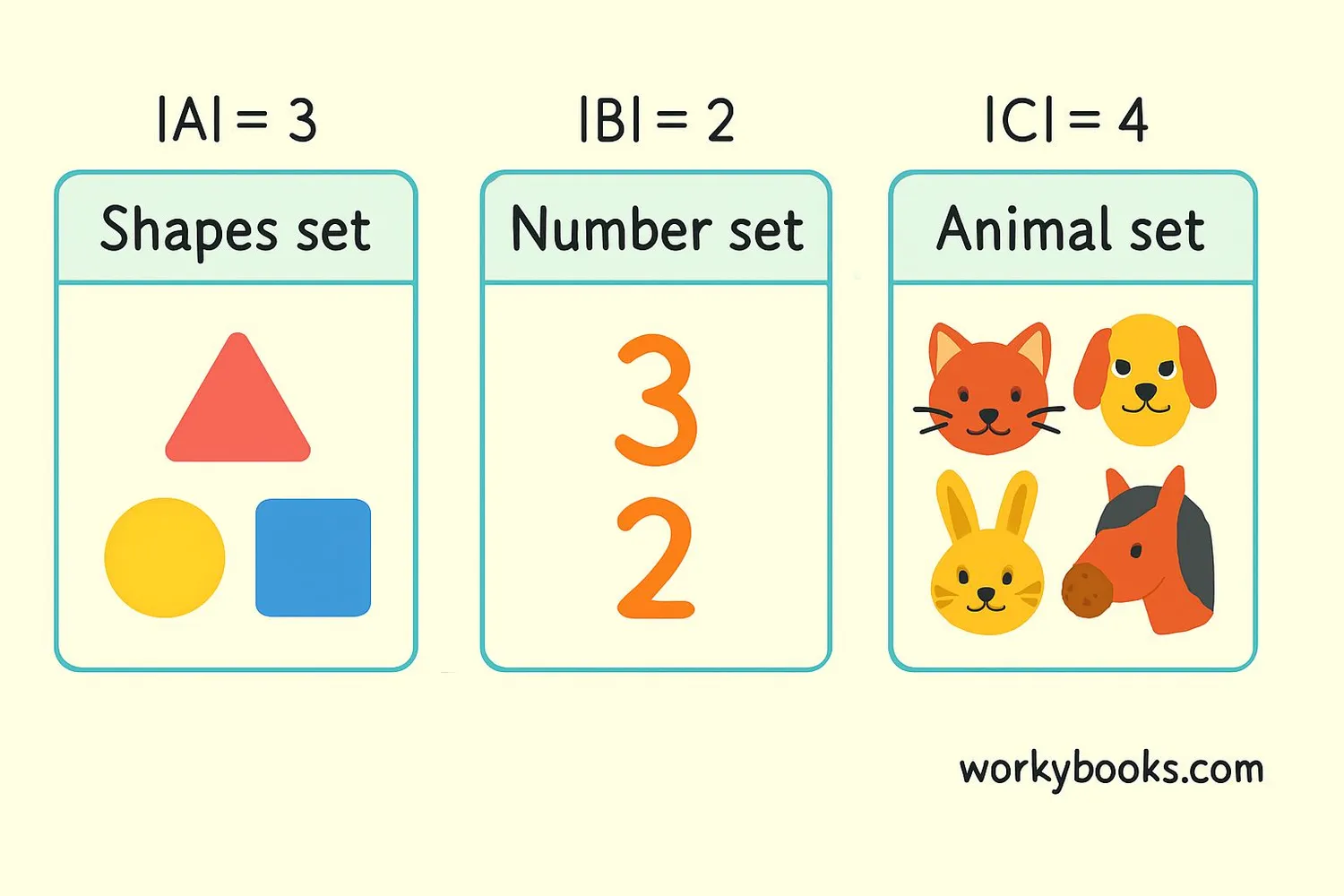
Let's practice finding cardinality with some examples:
Example 1: Set C = {circle, square, triangle, rectangle}
How many shapes? 4 different shapes → Cardinality = 4
Example 2: Set D = {2, 4, 6, 8, 10}
How many numbers? 5 different numbers → |D| = 5
Example 3: Set E = {red, red, blue, blue, blue, green}
How many colors? Only 3 unique colors (red, blue, green) → n(E) = 3
Example 4: Set F = {}
This is the empty set → |F| = 0
Example 5: Set G = {a, b, c, a, b, a}
How many letters? Only 3 unique letters (a, b, c) → n(G) = 3
Practice Tip
Make your own sets! Collect toys, colored blocks, or drawings and practice finding their cardinality.
Cardinality Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about set cardinality:
Math Trivia
Discover interesting facts about sets and mathematics:
Set Theory Origins
Set theory was developed by Georg Cantor in the 1870s. He was the first to define sets formally and study their properties mathematically.
Infinite Sets
Some sets have infinite cardinality! The set of natural numbers {1, 2, 3, ...} is infinite, and its cardinality is called "aleph-null".
Sets in Computers
Sets are fundamental in computer science. Databases use sets to store information, and programming languages have special data types for sets.
Largest Number Set
The largest named set in mathematics contains all possible sets - it's called the "universal set". Its cardinality is bigger than any number!





