Cartesian Plane - Definition, Examples, Quiz, FAQ, Trivia
Learn to navigate the world of coordinates with activities and quizzes!
What is the Cartesian Plane?
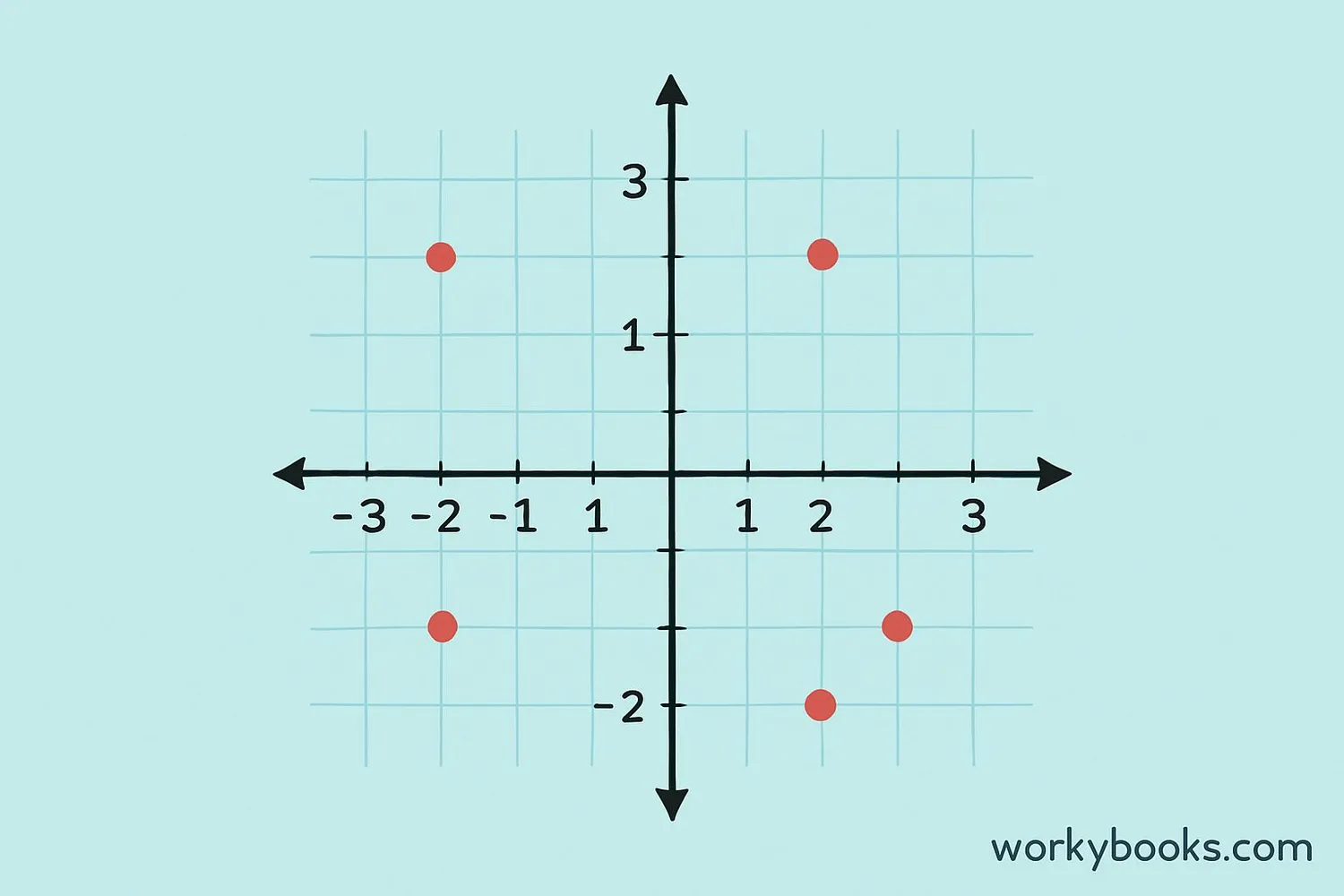
The Cartesian Plane, also called the coordinate plane, is a special grid system created by the mathematician René Descartes. It helps us locate points in space using two numbers called coordinates.
Imagine a map that uses two number lines that cross each other at zero. The horizontal line is called the x-axis and the vertical line is called the y-axis. Where they meet is called the origin.
Every point on the plane is described by an ordered pair of numbers (x, y). The first number (x) tells us how far to move left or right from the origin. The second number (y) tells us how far to move up or down.
Key Concept
The Cartesian Plane uses two perpendicular number lines to create a grid where every point has a unique address called an ordered pair (x, y).
Parts of the Cartesian Plane
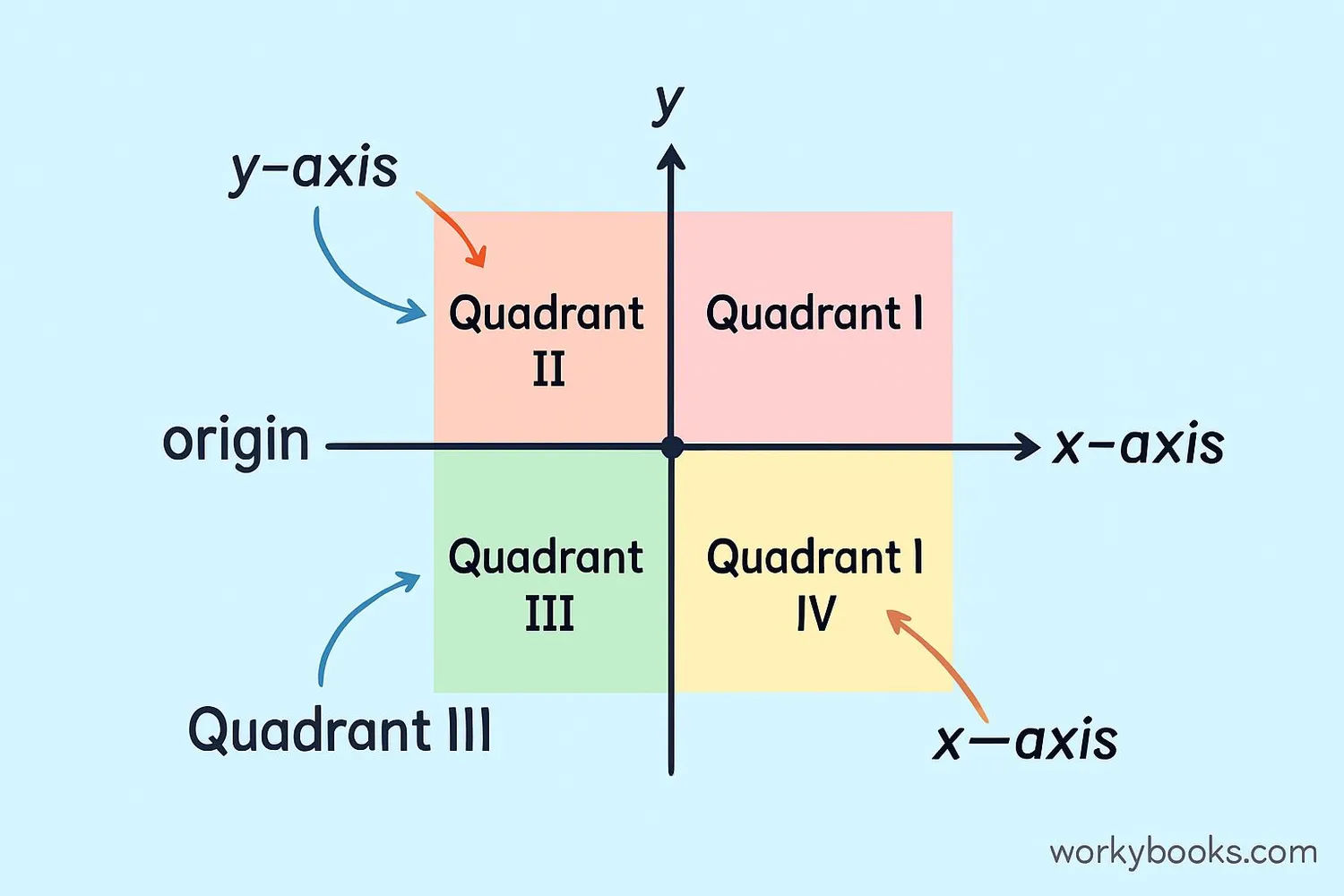
The Cartesian Plane has several important parts that work together:
X-axis: The horizontal number line. Positive numbers are to the right of the origin, negative numbers to the left.
Y-axis: The vertical number line. Positive numbers are above the origin, negative numbers below.
Origin (0,0): The point where the x-axis and y-axis cross. This is the center of the coordinate plane.
Ordered Pair: A pair of numbers (x,y) that describes a point's location. The first number is the abscissa (x-coordinate), the second is the ordinate (y-coordinate).
Quadrants: The plane is divided into four sections called quadrants, numbered I through IV in a counter-clockwise direction.
Remember
When writing coordinates, always put the x-value first, then the y-value: (x, y). Think "x comes before y in the alphabet."
How to Plot Points
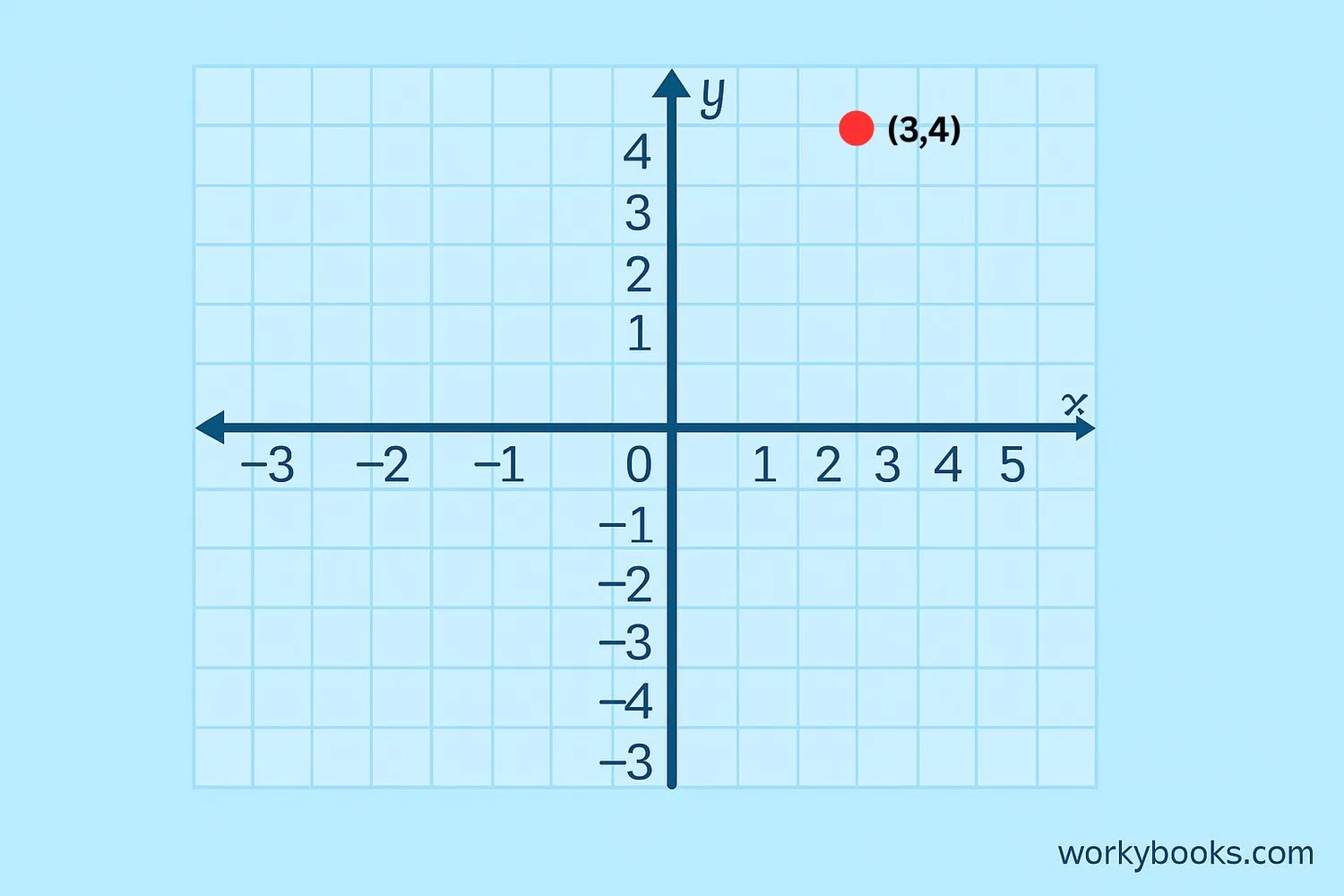
Plotting points on the Cartesian Plane is like following treasure map directions! Here's how to plot the point (3,4):
Step 1: Start at the origin (0,0)
Step 2: Move horizontally along the x-axis to the number 3
Step 3: From there, move vertically 4 units up (since 4 is positive)
Step 4: Place a dot where you end up - that's your point!
Remember:
- Positive x-values: move RIGHT from origin
- Negative x-values: move LEFT from origin
- Positive y-values: move UP from x-axis
- Negative y-values: move DOWN from x-axis
Coordinate System Rule
The first number moves you horizontally, the second number moves you vertically.
Understanding Quadrants
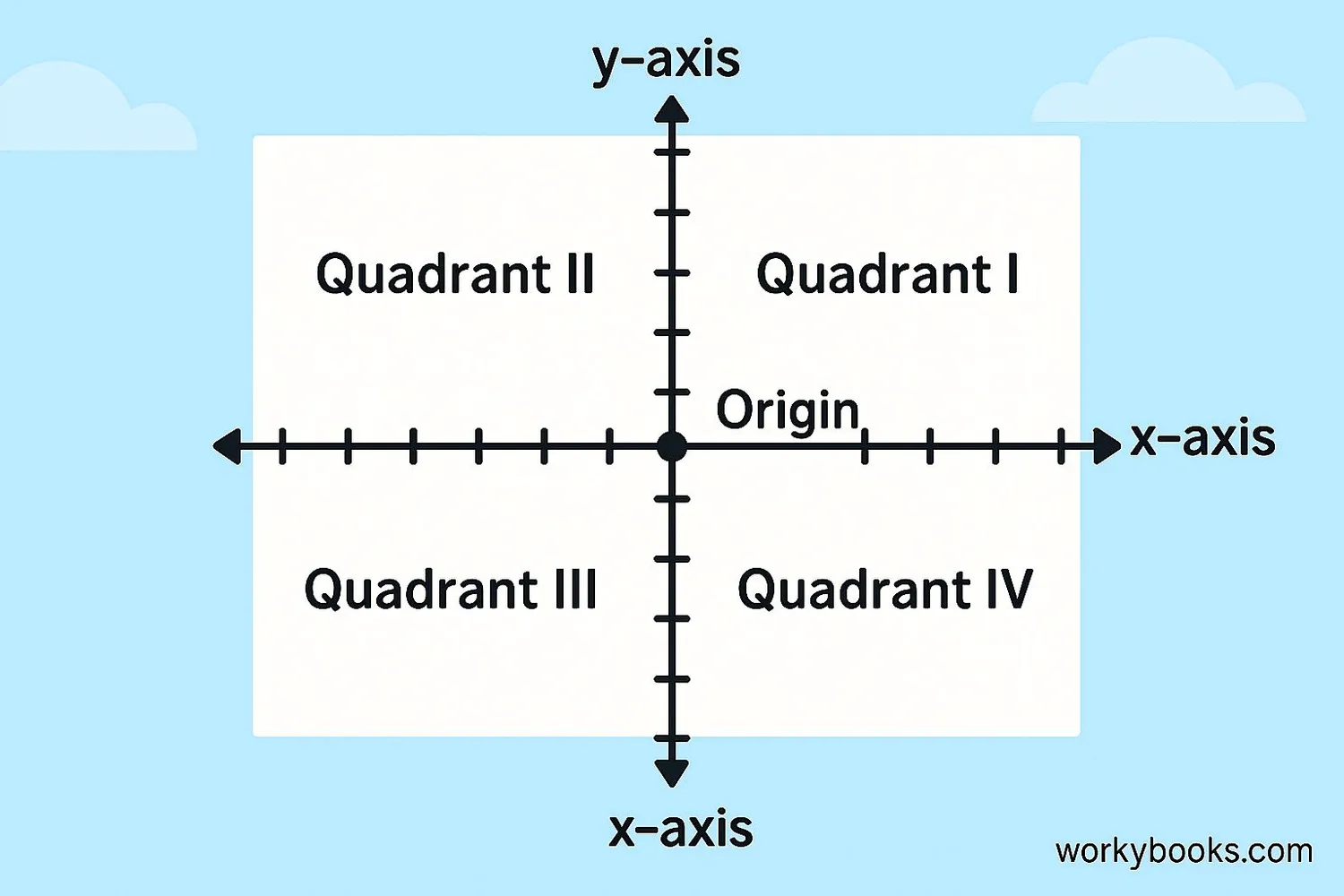
The Cartesian Plane is divided into four regions called quadrants. They help us understand the signs of coordinates:
Quadrant I (Top Right): Both x and y are positive (+,+)
Example: (3, 4)
Quadrant II (Top Left): x is negative, y is positive (-,+)
Example: (-2, 5)
Quadrant III (Bottom Left): Both x and y are negative (-,-)
Example: (-1, -3)
Quadrant IV (Bottom Right): x is positive, y is negative (+,-)
Example: (4, -2)
The quadrants are numbered counter-clockwise starting from the top right.
Memory Tip
To remember quadrant order: "All Students Take Calculus" - Quadrant I: All signs positive, Quadrant II: Sine positive, Quadrant III: Tangent positive, Quadrant IV: Cosine positive.
Real-World Examples
The Cartesian Plane isn't just for math class! We use coordinate systems in many everyday situations:
Maps and Navigation: GPS systems use coordinates to pinpoint locations. Street maps have grid systems with letters and numbers.
Video Games: Game designers use coordinates to position characters and objects on the screen.
Architecture: Blueprints use coordinate systems to specify exact locations for walls, windows, and doors.
Science: Scientists plot data points to show relationships between variables, like temperature changes over time.
Art: Digital artists use coordinate systems to create and manipulate images on computers.
Activity Idea
Create your own coordinate grid on graph paper and plot points to draw a picture or map of your classroom!
Coordinate Plane Quiz
Test your knowledge of the Cartesian Plane with these questions:
Frequently Asked Questions
Here are answers to common questions about the Cartesian Plane:
Math Trivia
Discover interesting facts about coordinate geometry:
Descartes' Dream
René Descartes claimed he conceived the coordinate system after watching a fly walk across his ceiling. He realized he could describe the fly's position using two numbers relative to the corners of his ceiling.
GPS Coordinates
The Global Positioning System (GPS) uses a three-dimensional coordinate system to pinpoint locations on Earth. Your phone receives signals from satellites to calculate your exact (x,y,z) position on our planet!
Negative Numbers Acceptance
The Cartesian Plane helped mathematicians accept negative numbers. Before Descartes, many mathematicians refused to work with negative values. The visual representation on the coordinate plane made negative numbers more understandable.
Battleship Game
The classic game Battleship uses a simplified Cartesian coordinate system! Players call out grid coordinates (like "B5") to target their opponent's ships. This makes it a great way to practice coordinate skills.





