Center of Rotation - Definition, Examples, Quiz, FAQ, Trivia
Learn about rotational symmetry, transformations, and how to find the fixed point of rotation
What is Center of Rotation?
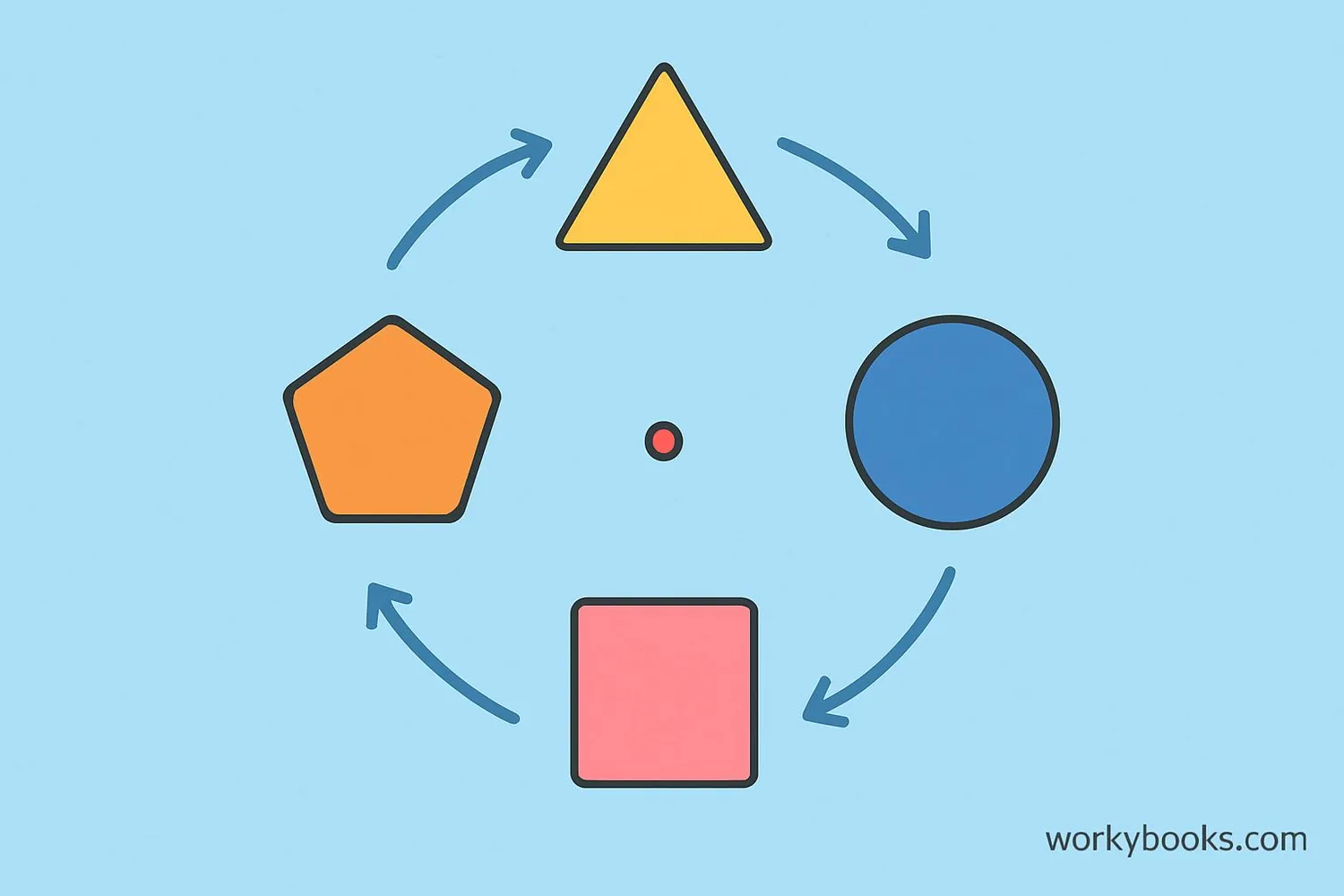
The center of rotation is the fixed point around which a shape or object rotates. When something turns, it spins around one point that doesn't move. This point is like the center of a merry-go-round where everything else moves around it.
Imagine spinning a pinwheel. The point where you hold it with your finger is the center of rotation. Everything else moves in a circle around that fixed point.
In mathematics, we use the center of rotation to describe how shapes move in a circular path without changing their size or shape. This is called a rotation transformation.
Key Concept
The center of rotation is the only point that doesn't move during a rotation. All other points move in circular paths around this fixed point.
Rotational Symmetry
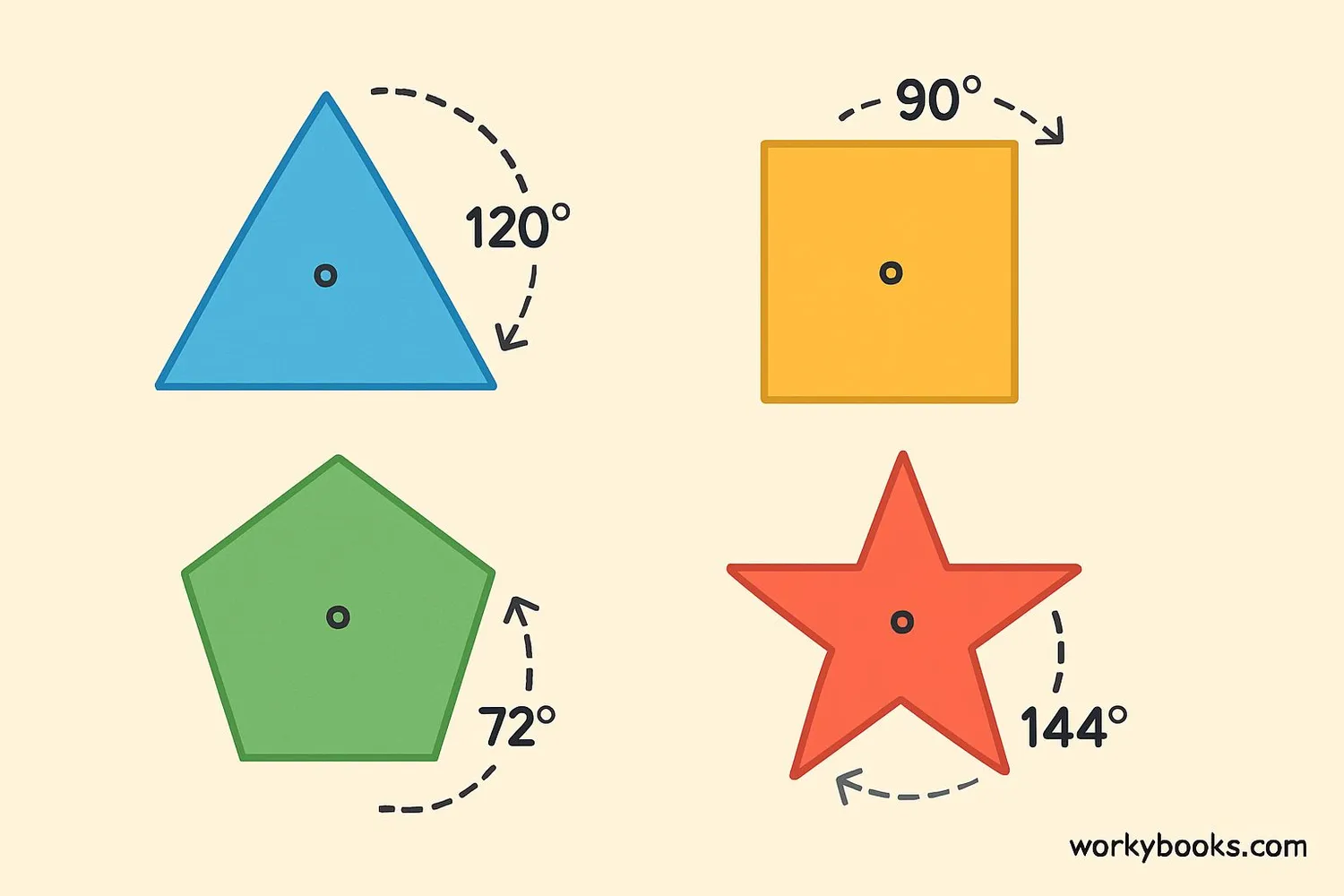
A shape has rotational symmetry if you can rotate it around its center point and it looks exactly the same in different positions. The number of times the shape matches its original position during a full 360° turn is called the order of rotational symmetry.
Examples:
- A circle has infinite rotational symmetry - it looks the same at any rotation angle
- A square has rotational symmetry of order 4 - it looks the same every 90° (¼ turn)
- An equilateral triangle has rotational symmetry of order 3 - it looks the same every 120° (⅓ turn)
The angle of rotation is how many degrees you turn the shape to make it look the same. For a shape with order n, the angle of rotation is 360°/n.
Remember
For a shape to have rotational symmetry, it must look identical after rotation without flipping or resizing.
Finding the Center of Rotation
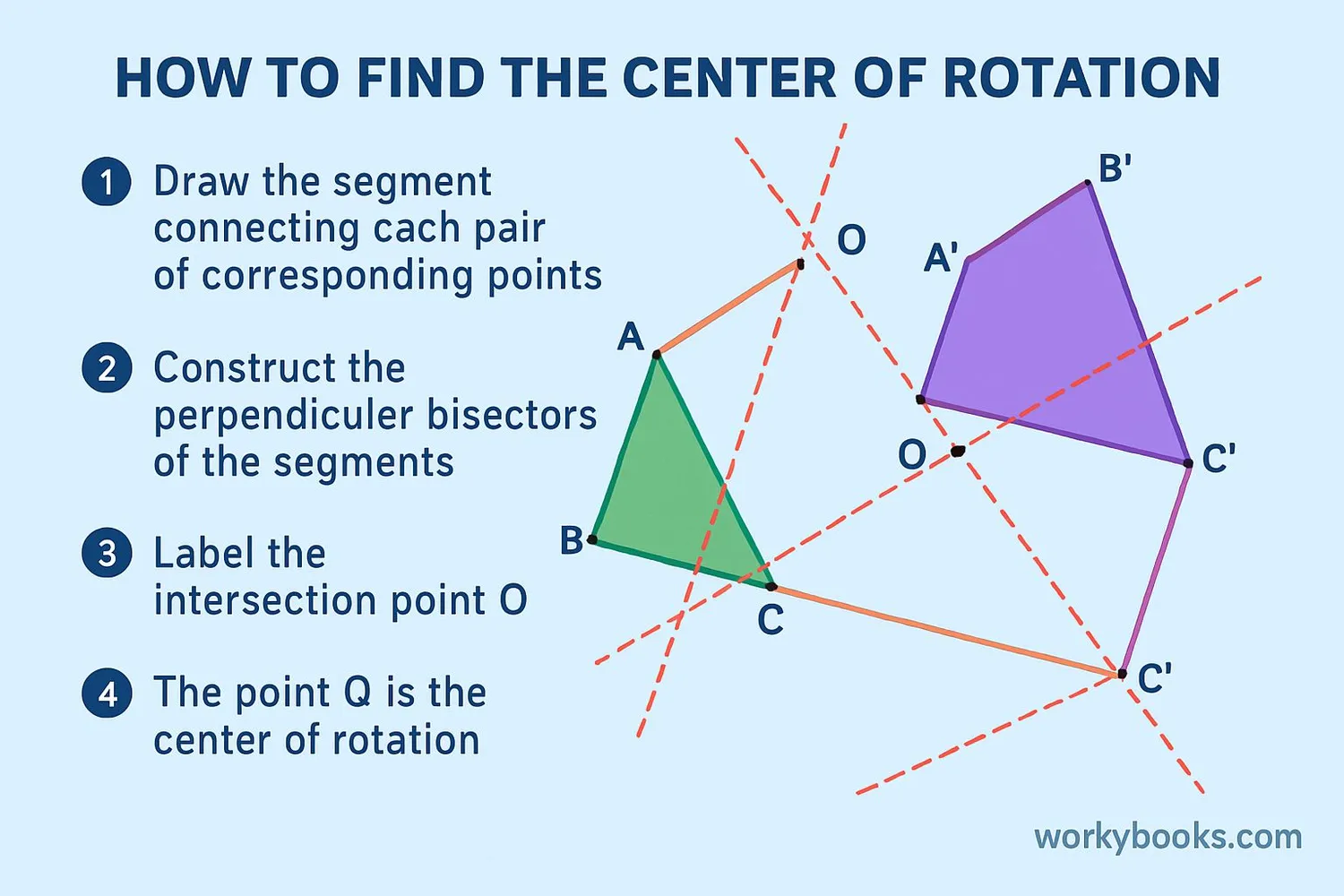
How do we find the center of rotation between two identical shapes? Here's a simple method:
Step-by-step:
- Choose two corresponding points on the original shape and the rotated shape
- Draw a straight line connecting these two points
- Find the perpendicular bisector of this line (the line that cuts it exactly in half at a right angle)
- Repeat with another pair of corresponding points
- The point where the two perpendicular bisectors cross is the center of rotation!
This works because during rotation, every point moves in a circle around the center. The center must be equally distant from each point and its rotated position.
Tip
You only need two pairs of points to find the center of rotation. The more points you use, the more accurate your center will be.
Rotation in the Coordinate Plane
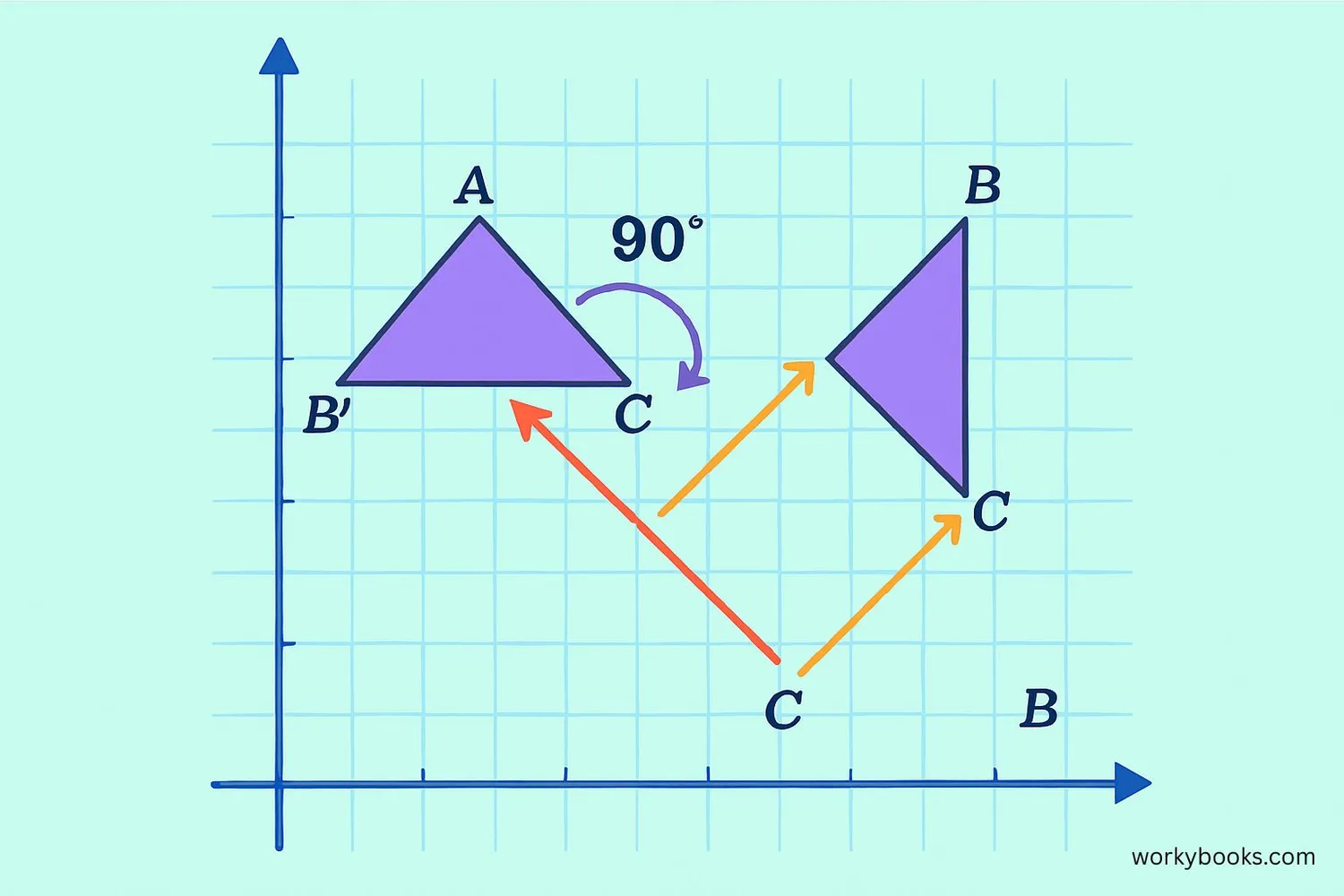
When we rotate shapes on a coordinate plane, we use the center of rotation and an angle to determine new positions. The origin (0,0) is often used as the center, but we can rotate around any point.
Common rotation rules (around origin):
- 90° clockwise: (x, y) → (y, -x)
- 90° counterclockwise: (x, y) → (-y, x)
- 180°: (x, y) → (-x, -y)
- 270° clockwise: (x, y) → (-y, x)
To rotate around a different center point, we:
- Subtract the center coordinates from our point
- Apply the rotation rule
- Add the center coordinates back
Rotation Formula
Where (x₀, y₀) is the center of rotation and θ is the rotation angle
Rotation Knowledge Quiz
Test your understanding of center of rotation with these questions:
Frequently Asked Questions
Here are answers to common questions about rotation:
Rotation Trivia
Discover interesting facts about rotation:
Earth's Rotation
Earth rotates at about 1,670 km/h at the equator! But you don't feel it because everything around you is moving at the same speed.
Plant Rotation
Sunflowers rotate during the day to face the sun in a process called heliotropism. At night, they rotate back to face east for sunrise!
Rotational Symmetry Record
A circle has infinite rotational symmetry! It looks identical no matter how much you rotate it around its center.
Fastest Rotation
The fastest man-made rotating object is a tiny dumbbell-shaped nanoparticle that spins at 300 billion rotations per minute!





