Circles - Definition, Examples, Quiz, FAQ, Trivia
Learn about circles, their properties, and how to calculate area and circumference with simple explanations and activities
What is a Circle?
A circle is a special shape where every point along its edge is exactly the same distance from the center. This makes it perfectly round with no corners or edges. Circles are all around us - wheels, clocks, and even pizzas are shaped like circles!
Circles are important in geometry because they're symmetrical and have special properties that other shapes don't have. Mathematicians have studied circles for thousands of years.
The distance from the center to the edge is called the radius. The distance straight across the circle through the center is called the diameter. The distance around the circle is called the circumference.
Key Fact
A circle is defined by its center point and radius. Every point on the circle is exactly the radius distance from the center.
Parts of a Circle
Circles have several important parts that help us understand and measure them:
The middle point of the circle
Distance from center to edge
Distance across through center
Line connecting two points
Radius: The distance from the center to any point on the circle. All radii in a circle are equal.
Diameter: A straight line passing through the center that connects two points on the circle. The diameter is always twice the radius.
Circumference: The distance around the circle. This is like the perimeter of circular shapes.
Chord: A straight line connecting any two points on the circle. The diameter is the longest possible chord.
Relationship
Diameter = 2 × Radius. If you know the radius, you can find the diameter, and vice versa.
Area of a Circle
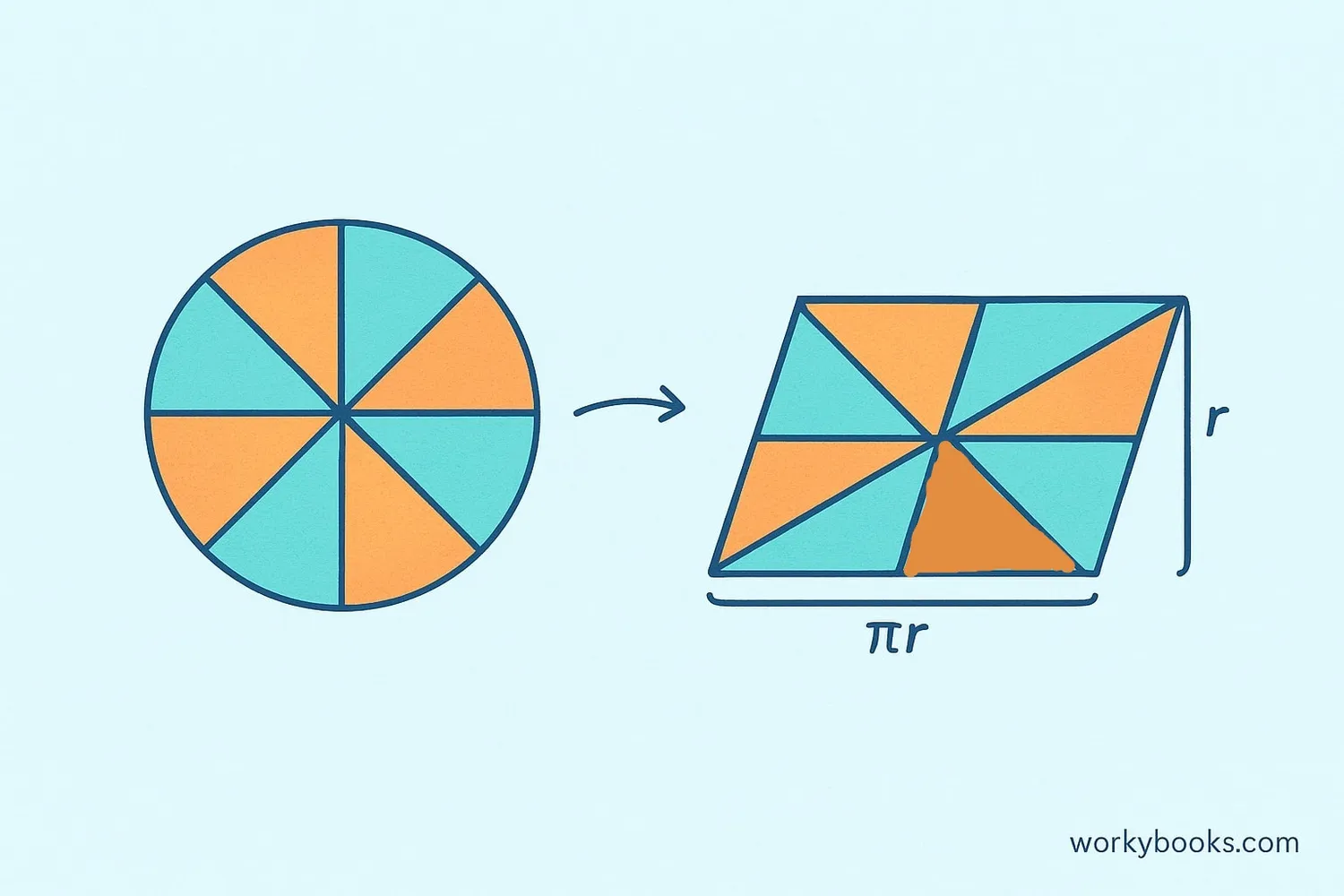
The area of a circle is the space inside the circle. We measure area in square units like cm² or in². The formula for calculating the area of a circle is:
Area Formula
Where A is area, π (pi) is approximately 3.14, and r is the radius.
Example: What's the area of a circle with a radius of 5 cm?
Step 1: Start with the formula → A = π × r²
Step 2: Plug in the values → A = 3.14 × (5 × 5)
Step 3: Calculate → 3.14 × 25 = 78.5 cm²
So the area is 78.5 square centimeters.
Remember
The area formula uses radius squared. If you're given the diameter, remember to divide it by 2 to get the radius first!
Circumference of a Circle

The circumference is the distance around a circle - like the perimeter of circular shapes. The formula for circumference is:
Circumference Formula
or
Where C is circumference, π (pi) is approximately 3.14, d is diameter, and r is radius.
Example: What's the circumference of a circle with a diameter of 10 cm?
Step 1: Use the formula → C = π × d
Step 2: Plug in the values → C = 3.14 × 10
Step 3: Calculate → 31.4 cm
So the circumference is 31.4 centimeters.
Why π (pi)? Pi is a special number that represents the relationship between a circle's circumference and its diameter. For any circle, if you divide the circumference by the diameter, you always get pi (approximately 3.14).
Pi (π) Facts
Pi is an irrational number that goes on forever without repeating. We usually use 3.14 or 22/7 for calculations.
Circle Knowledge Quiz
Test your understanding of circles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about circles:
Circle Trivia
Discover interesting facts about circles:
Ancient Circles
The earliest known circle drawings date back over 5,000 years! Stonehenge in England, built around 2500 BCE, has circular patterns that align with the sun and moon.
Nature's Circles
Circles appear everywhere in nature - from tree rings and ripples in water to planets and stars. Even your pupils are circular!
Pi Calculation
Computers have calculated pi to over 100 trillion digits! You only need about 40 digits to measure the circumference of the entire universe with accuracy to the size of an atom.
Largest Circle
The largest human-made circle is the Large Hadron Collider in Switzerland. This underground circle is 27 kilometers (about 17 miles) in circumference!


