Circumference of a Circle - Definition, Examples, Quiz, FAQ, Trivia
Learn about circle measurements with easy explanations, formulas, and practice activities
What is Circumference?
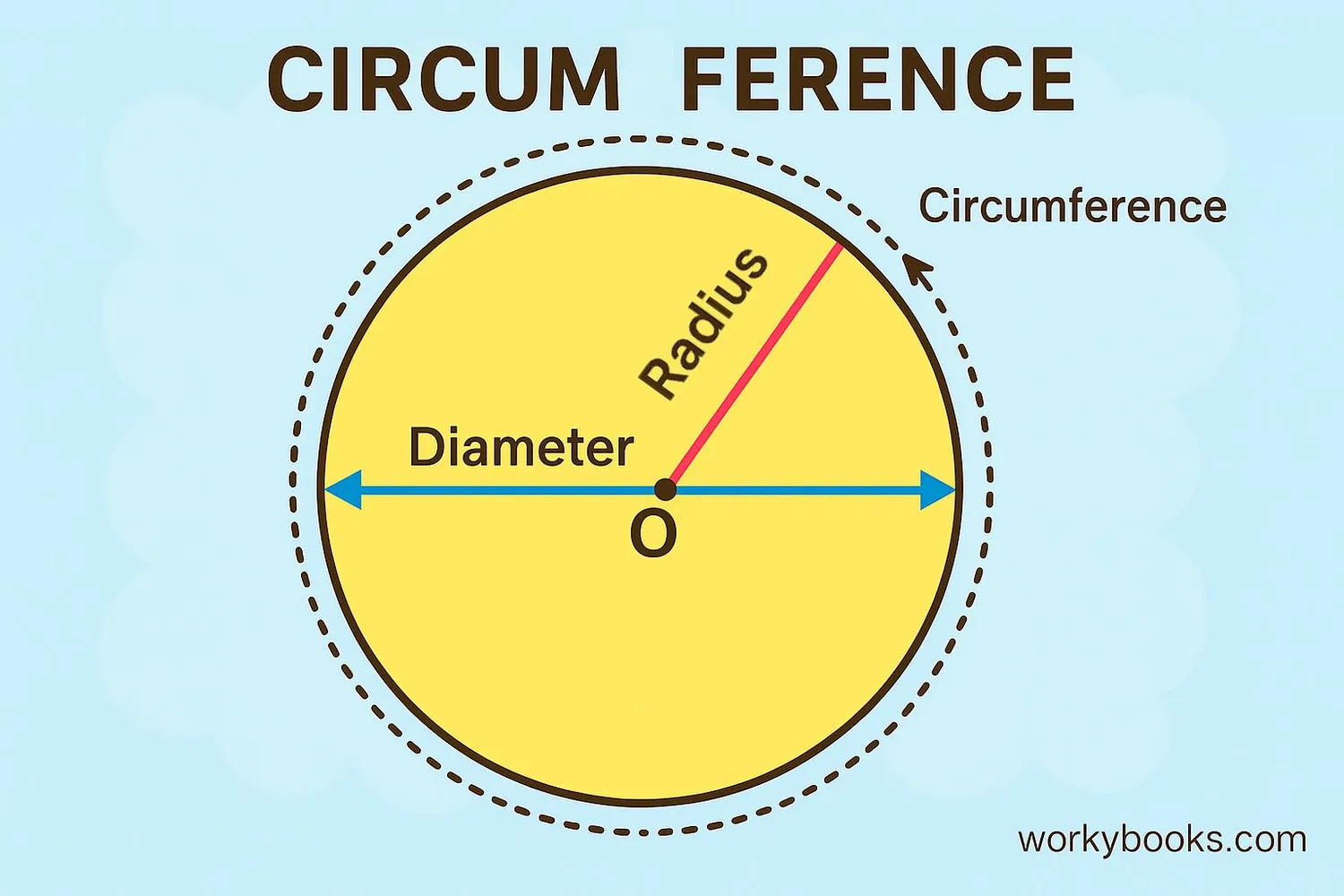
The circumference of a circle is the distance around its outer edge. Think of it as the perimeter of the circle.
Why is this important? Knowing the circumference helps us understand the size of circular objects like wheels, plates, or planets.
Imagine wrapping a string around a circle. The length of that string would be the circle's circumference. It's different from the area, which measures the space inside the circle.
Key Concept
Circumference is to circles what perimeter is to rectangles and squares. It's the total distance around the circle.
Parts of a Circle

To understand circumference, we need to know these important parts of a circle:
Distance from center to edge
Distance across circle through center
Distance around the circle
Diameter (d) is always twice the radius (r). This means d = 2 × r or r = d ÷ 2.
The relationship between these parts is what makes it possible to calculate circumference using mathematical formulas.
Remember
The diameter is always twice as long as the radius. If you know one, you can find the other!
Circumference Formula
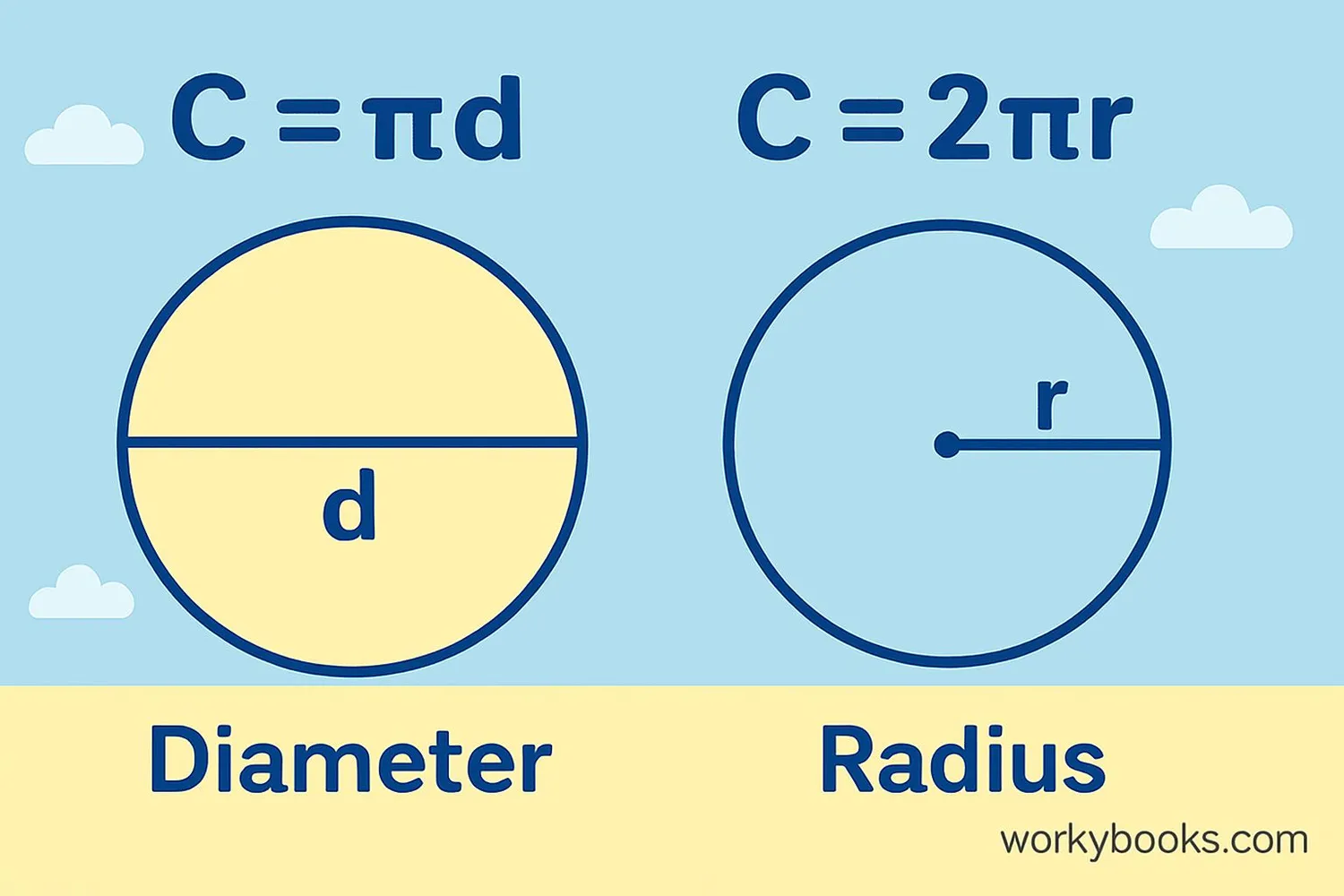
To calculate the circumference, we use a special number called Pi (π). Pi is approximately 3.14, but it's actually an endless number that starts with 3.14159...
There are two main formulas for circumference:
Circumference Formulas
(Circumference = Pi times Diameter)
(Circumference = 2 times Pi times Radius)
Since diameter (d) is twice the radius (r), both formulas give the same result. You can use whichever is more convenient based on what measurement you have.
Example: For a circle with radius 5 cm:
C = 2 × π × r = 2 × 3.14 × 5 ≈ 31.4 cm
or using diameter (d = 10 cm):
C = π × d = 3.14 × 10 = 31.4 cm
Pi Tip
For most calculations, using π ≈ 3.14 is accurate enough. For more precision, use 3.1416 or the π button on a calculator.
Real-World Examples
Let's practice calculating circumference with real-world examples:
Example 1: A bicycle wheel has a diameter of 70 cm. What is its circumference?
Solution: C = π × d = 3.14 × 70 ≈ 219.8 cm
Example 2: A circular table has a radius of 45 cm. How much trim is needed to go around it?
Solution: C = 2 × π × r = 2 × 3.14 × 45 ≈ 282.6 cm
Example 3: A pizza has a circumference of 94.2 cm. What is its diameter?
Solution: Since C = π × d, then d = C ÷ π = 94.2 ÷ 3.14 ≈ 30 cm
Example 4: A Ferris wheel has a radius of 15 meters. How far do you travel in one complete rotation?
Solution: C = 2 × π × r = 2 × 3.14 × 15 ≈ 94.2 meters
Conversion Tip
To find the diameter when you know circumference, divide by π. To find radius, divide by 2π.
Circumference Practice Quiz
Test your circle knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about circumference:
Circle Trivia
Discover interesting facts about circles and circumference:
The Never-Ending Pi
Pi (π) is an irrational number, meaning its decimal representation never ends and never repeats. Mathematicians have calculated over 62 trillion digits of pi, but we only need a few digits for most calculations.
Ancient Circle Knowledge
The ancient Egyptians and Babylonians knew about pi over 4,000 years ago! The Rhind Papyrus (1650 BCE) shows Egyptians used a value of 3.1605 for π, which is very close to the actual value.
Circles in Nature
Circles appear everywhere in nature - from tree rings and bubbles to planets and stars. The circular shape allows for maximum area with minimum perimeter, making it energy-efficient for many natural structures.
Earth's Circumference
The Earth's circumference at the equator is about 40,075 km (24,901 miles). Ancient Greek mathematician Eratosthenes calculated this over 2,200 years ago using shadows and geometry!





