Congruence of Triangles - Definition, Examples, Quiz, FAQ, Trivia
Learn about congruent triangles with easy explanations, theorems, examples, and practice activities
What is Congruence of Triangles?
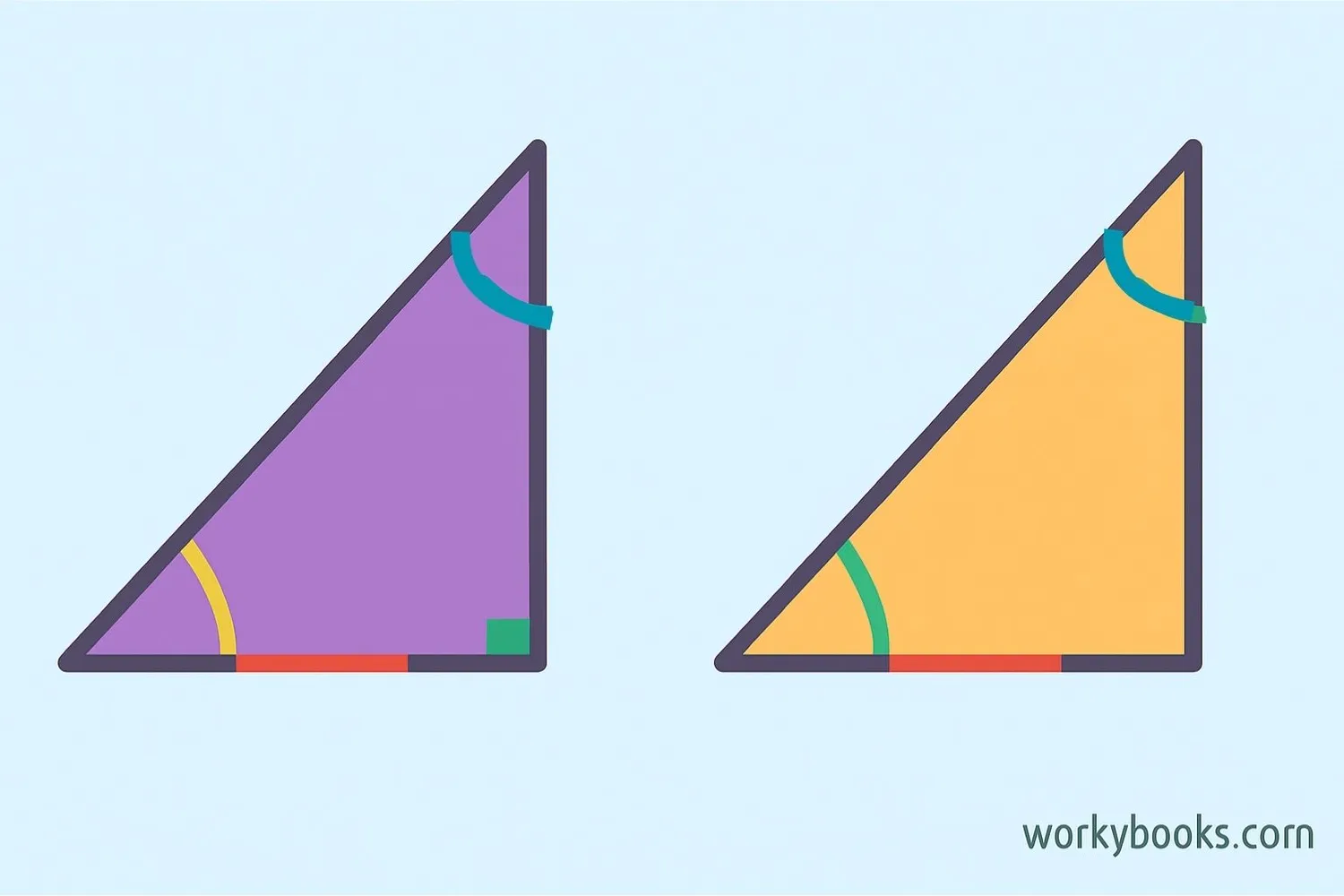
Two triangles are congruent when they have exactly the same size and shape. This means:
- All three sides of one triangle are equal to the corresponding sides of the other triangle
- All three angles of one triangle are equal to the corresponding angles of the other triangle
When triangles are congruent, we can say they are identical copies of each other. The symbol for congruence is ≅.
For example, if triangle ABC is congruent to triangle DEF, we write it as: △ABC ≅ △DEF.
Key Concept
Congruent triangles will always have the same area and perimeter because their sides and angles are identical.
Triangle Congruence Theorems
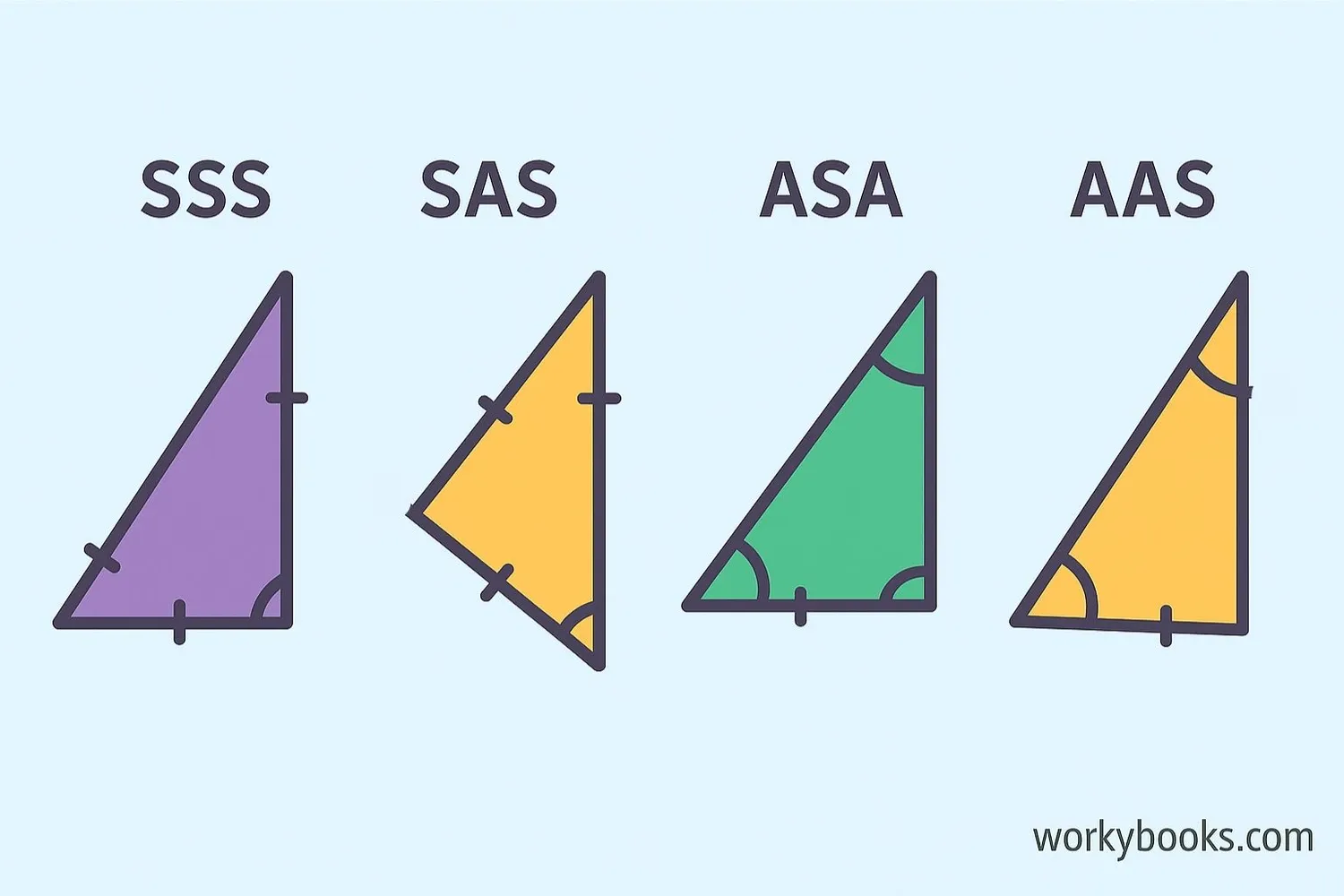
We don't always need to check all six parts (three sides and three angles) to prove triangles are congruent. Mathematicians have discovered special rules called congruence theorems that allow us to prove congruence with just three matching parts.
SSS Theorem
Side-Side-Side (SSS): If all three sides of one triangle are equal to the corresponding three sides of another triangle, then the triangles are congruent.
SAS Theorem
Side-Angle-Side (SAS): If two sides and the included angle of one triangle are equal to two sides and the included angle of another triangle, then the triangles are congruent.
ASA Theorem
Angle-Side-Angle (ASA): If two angles and the included side of one triangle are equal to two angles and the included side of another triangle, then the triangles are congruent.
AAS Theorem
Angle-Angle-Side (AAS): If two angles and a non-included side of one triangle are equal to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
Important Note
SSA (Side-Side-Angle) is NOT a congruence theorem. Two triangles with two sides and a non-included angle equal may not be congruent!
Examples of Congruent Triangles

Let's look at some examples of congruent triangles:
Example 1: SSS Congruence
Triangle ABC has sides AB=5cm, BC=7cm, AC=6cm. Triangle DEF has sides DE=5cm, EF=7cm, DF=6cm. Since all three sides are equal, △ABC ≅ △DEF by SSS theorem.
Example 2: SAS Congruence
Triangle PQR has PQ=8cm, ∠P=60°, PR=10cm. Triangle XYZ has XY=8cm, ∠X=60°, XZ=10cm. Since two sides and the included angle are equal, △PQR ≅ △XYZ by SAS theorem.
Example 3: ASA Congruence
Triangle LMN has ∠L=50°, LM=12cm, ∠M=70°. Triangle OPQ has ∠O=50°, OP=12cm, ∠P=70°. Since two angles and the included side are equal, △LMN ≅ △OPQ by ASA theorem.
Example 4: AAS Congruence
Triangle ABC has ∠A=40°, ∠B=60°, BC=9cm. Triangle DEF has ∠D=40°, ∠E=60°, EF=9cm. Since two angles and a non-included side are equal, △ABC ≅ △DEF by AAS theorem.
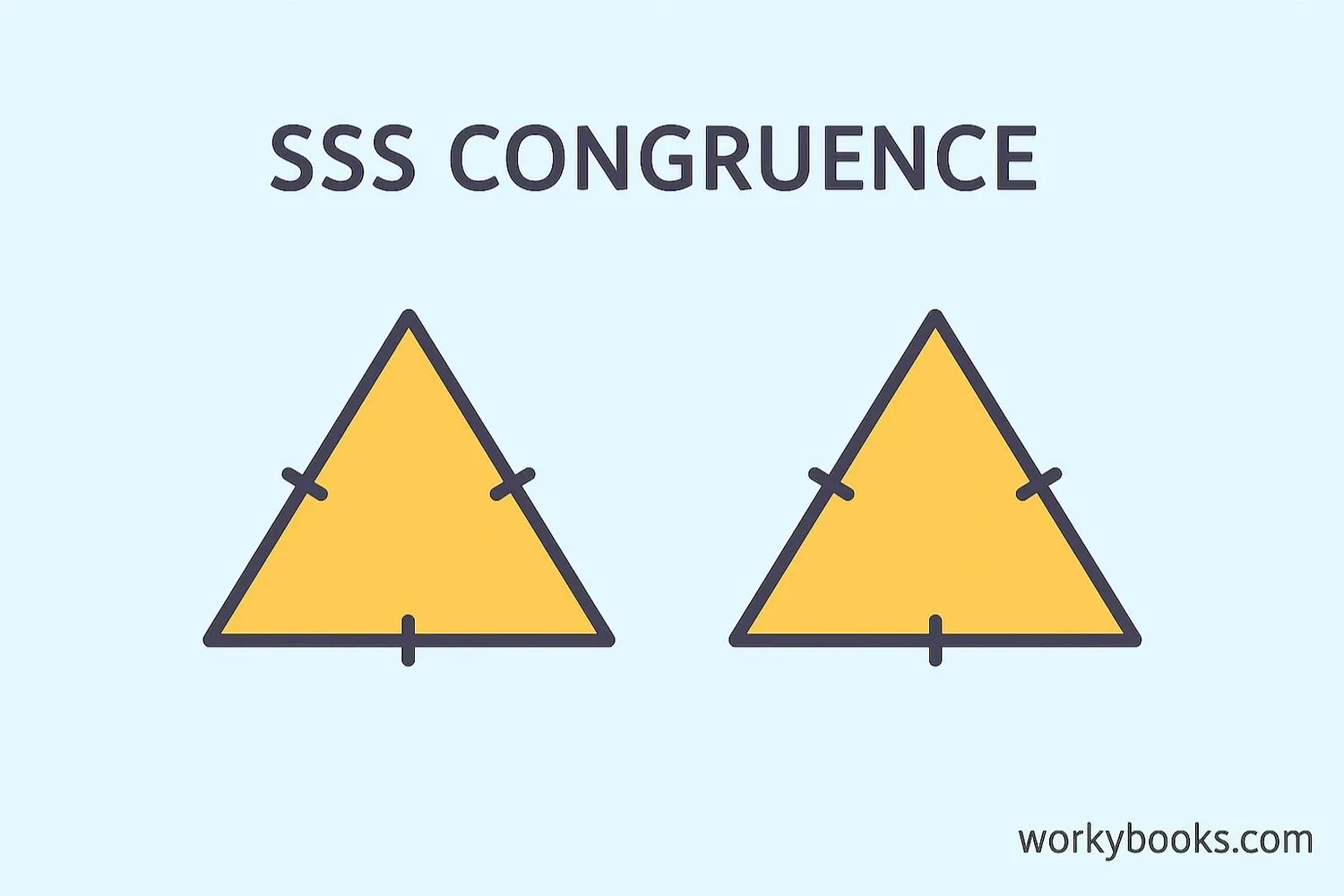
SSS Congruence
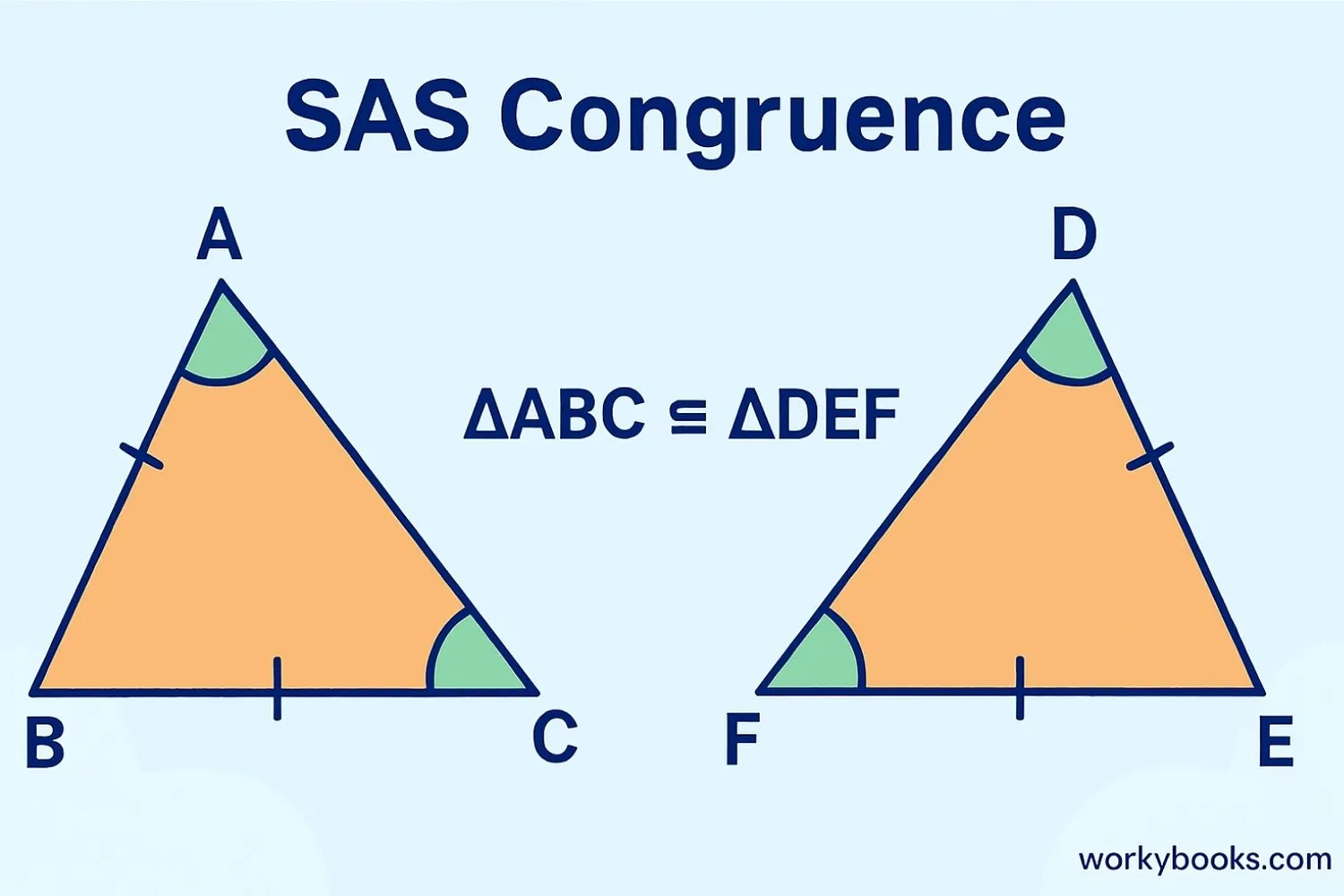
SAS Congruence
Proof Tip
When writing congruence proofs, always state the congruence theorem you're using and match the corresponding vertices in the same order.
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about congruent triangles:
Geometry Trivia
Discover interesting facts about triangles and congruence:
Ancient Geometry
The concept of congruent triangles was first recorded in ancient Egypt around 3000 BC, where surveyors used triangle congruence to re-establish field boundaries after the Nile River flooded.
Structural Strength
Triangles are the strongest geometric shape because their sides work together to distribute force evenly. This is why congruent triangular patterns are used in bridges, towers, and roofs.
Space Exploration
NASA engineers use triangle congruence principles when designing spacecraft components to ensure precise fittings and symmetrical weight distribution.
World's Largest Triangle
The largest man-made triangle is the triangular facade of the Luxor Hotel in Las Vegas, measuring 106 meters (348 feet) on each side of its base.





