Coplanar - Definition, Examples, Quiz, FAQ, Trivia
Learn how points and lines can lie on the same plane with easy explanations and practice activities
What is Coplanar?
In geometry, coplanar means that points, lines, or shapes all lie on the same flat surface, called a plane. A plane is like a perfectly flat sheet of paper that extends forever in all directions.
Think of a tabletop - anything that sits completely flat on that tabletop is coplanar with the table. If something sticks up above the table or hangs below it, it's not coplanar.
Coplanar Definition
Coplanar refers to points or lines that lie on the same geometric plane. Any two points are always coplanar, but three or more points might not be.
Key Concept
A plane is a flat, two-dimensional surface that extends infinitely in all directions. Coplanar objects all share the same plane.
Coplanar Points
Coplanar points are points that all lie on the same plane. Any two points are always coplanar because you can always draw a plane that contains both of them. With three or more points, they might or might not be coplanar.
For example, the four corners of a sheet of paper are coplanar because they all lie on the flat surface of the paper. But if you lift one corner up, those four points would no longer be coplanar.
Example
Look at the corners of your classroom's ceiling. The four points where the walls meet the ceiling are coplanar because they all lie on the same plane (the ceiling).
Remember
Any three points are always coplanar, but four or more points may or may not be coplanar.
Coplanar Lines

Coplanar lines are lines that lie on the same plane. When lines are coplanar, they can either be parallel, intersecting, or coincident (lying exactly on top of each other).
Two lines are always coplanar if they intersect or are parallel. But lines that never meet and aren't parallel (called skew lines) are not coplanar.
Example
The lines on notebook paper are coplanar because they all lie on the flat surface of the paper. The lines on a basketball court are also coplanar.
Important
If two lines are coplanar, they either intersect at exactly one point or are parallel (never intersect).
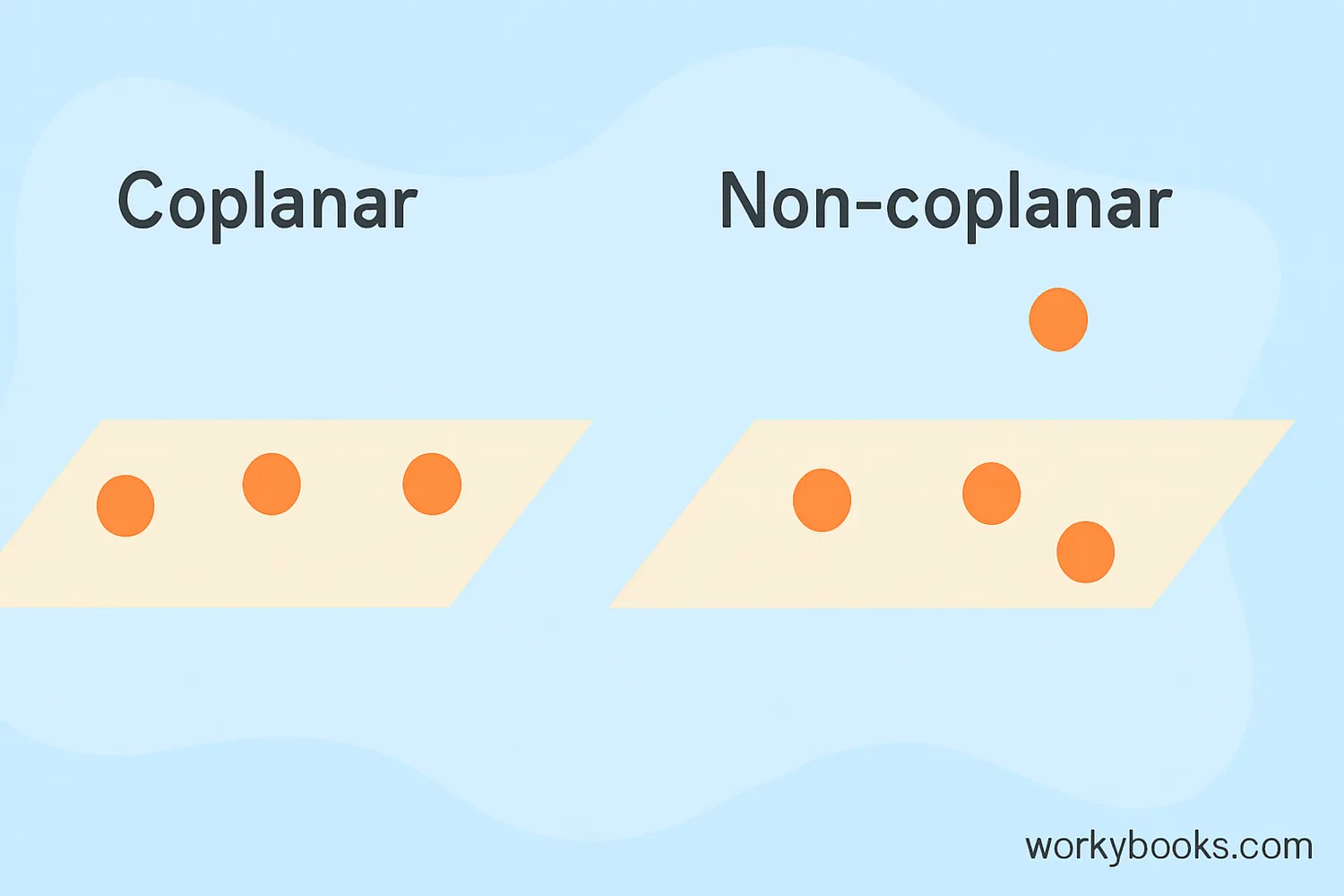
Non-Coplanar
Non-coplanar means that points or lines do not all lie on the same plane. They are in different planes or at different heights.
For example, the four legs of a chair might not be coplanar if the chair is on an uneven surface. The corners of a room (where two walls meet the ceiling) are non-coplanar with the corners of the floor.
Example
Imagine a cube. The four points on the top face are coplanar. The four points on the bottom face are also coplanar. But if you take one point from the top and one from the bottom, they are not coplanar with points from the sides.
Remember
In 3D space, most sets of four or more points are non-coplanar. They require at least two different planes to contain them all.
Coplanar Vectors

In math, a vector is a quantity that has both direction and magnitude (size). Coplanar vectors are vectors that lie on the same plane.
We can test if vectors are coplanar by seeing if they can be expressed as a combination of two other vectors in the plane. If three vectors are coplanar, the scalar triple product of these vectors is zero.
Test for Coplanarity
For three vectors a, b, and c, if their scalar triple product equals zero, they are coplanar.
Simplified
Imagine three arrows lying flat on a table. If you can slide them around without lifting them off the table to form a triangle, they're coplanar.
Coplanar Practice Quiz
Test your understanding of coplanar concepts with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about coplanar concepts:
Geometry Trivia
Discover interesting facts about geometry and planes:
Euclid's Elements
The concept of planes was first described by Euclid around 300 BCE in his book "Elements," which laid the foundation for geometry as we know it today.
Flat Earth Myth
Ancient Greeks proved Earth was round by observing ships disappear hull-first over the horizon. They used geometric principles to calculate Earth's circumference with surprising accuracy.
Chessboard Geometry
All 64 squares on a chessboard are coplanar because they lie on the same flat surface. The pieces move in geometric patterns following specific plane rules.
Largest Man-Made Plane
The flattest large man-made plane is the Salar de Uyuni salt flat in Bolivia. Spanning over 10,000 square kilometers, its surface varies by less than 1 meter in elevation.





