Corresponding Sides - Definition, Examples, Quiz, FAQ, Trivia
Learn to identify matching sides in congruent and similar shapes with easy explanations and practice activities
What are Corresponding Sides?
Corresponding sides are matching sides in different shapes that are in the same relative position. When we have two shapes that are congruent or similar, their corresponding sides have a special relationship.
Think of corresponding sides like matching socks - they go together because they're in the same position and have the same size (for congruent shapes) or proportional size (for similar shapes).
To find corresponding sides:
- Look at the angles of the shapes
- Sides opposite equal angles are corresponding sides
- Sides between the same angles are corresponding sides
Key Concept
Corresponding sides are always found in the same relative position in congruent or similar shapes.
Corresponding Sides in Congruent Triangles
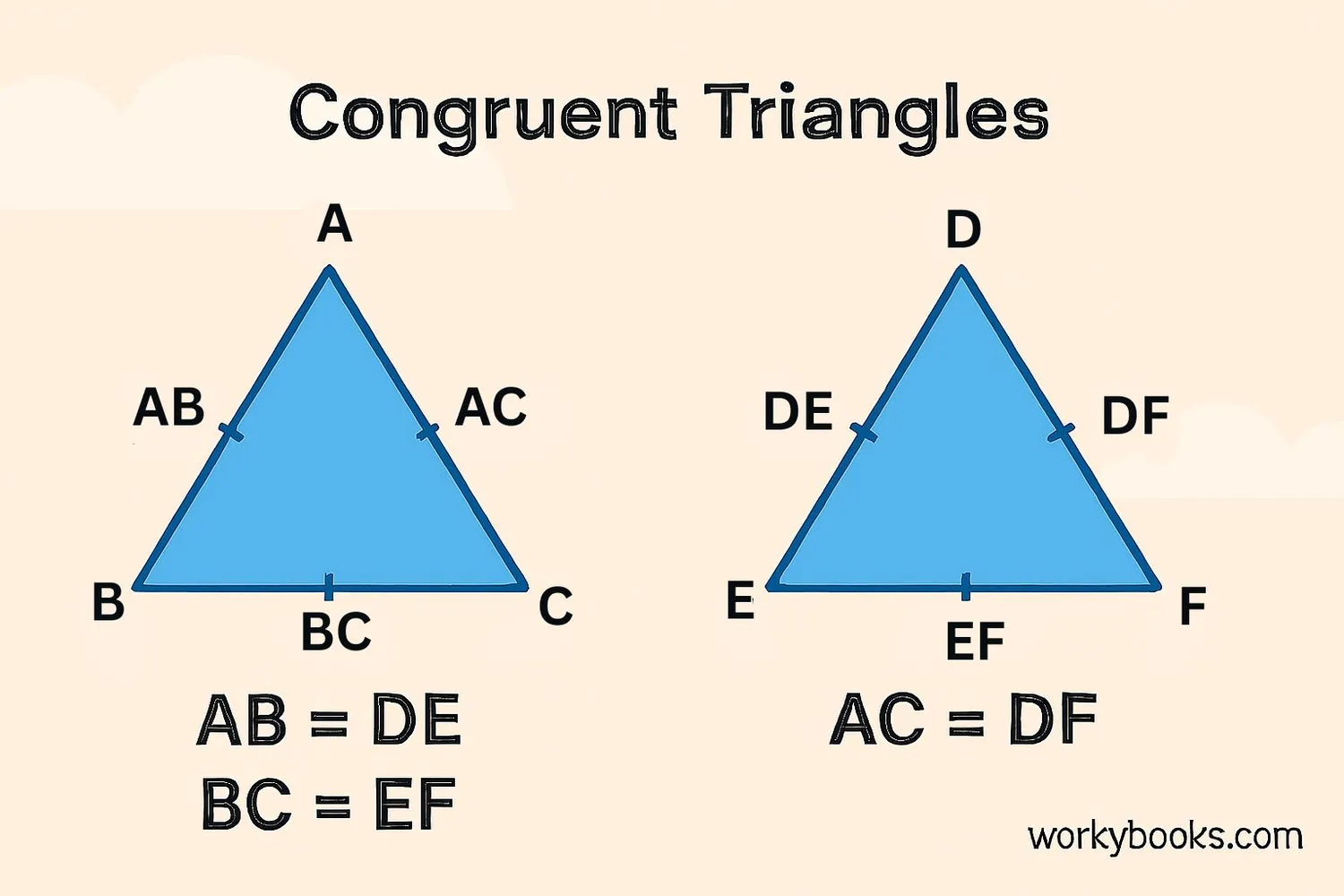
Congruent triangles are identical in shape and size. When triangles are congruent, their corresponding sides are equal in length and their corresponding angles are equal in measure.
Important Rule
For congruent triangles ΔABC ≅ ΔDEF, side AB corresponds to DE, BC to EF, and AC to DF.
- If triangles are congruent, their corresponding sides are equal
- If all three pairs of corresponding sides are equal, the triangles are congruent (SSS congruence)
- Corresponding sides help us solve geometry problems
Remember
In congruent triangles, corresponding sides are always equal in length.
Corresponding Sides in Similar Triangles

Similar triangles have the same shape but different sizes. Their corresponding angles are equal, and their corresponding sides are proportional.
Important Rule
For similar triangles ΔABC ~ ΔDEF, the ratio of corresponding sides is constant.
- Corresponding angles are equal: ∠A = ∠D, ∠B = ∠E, ∠C = ∠F
- Corresponding sides are proportional: AB/DE = BC/EF = AC/DF
- The constant ratio is called the scale factor
Remember
In similar triangles, corresponding sides are proportional but not necessarily equal in length.
Real-World Examples
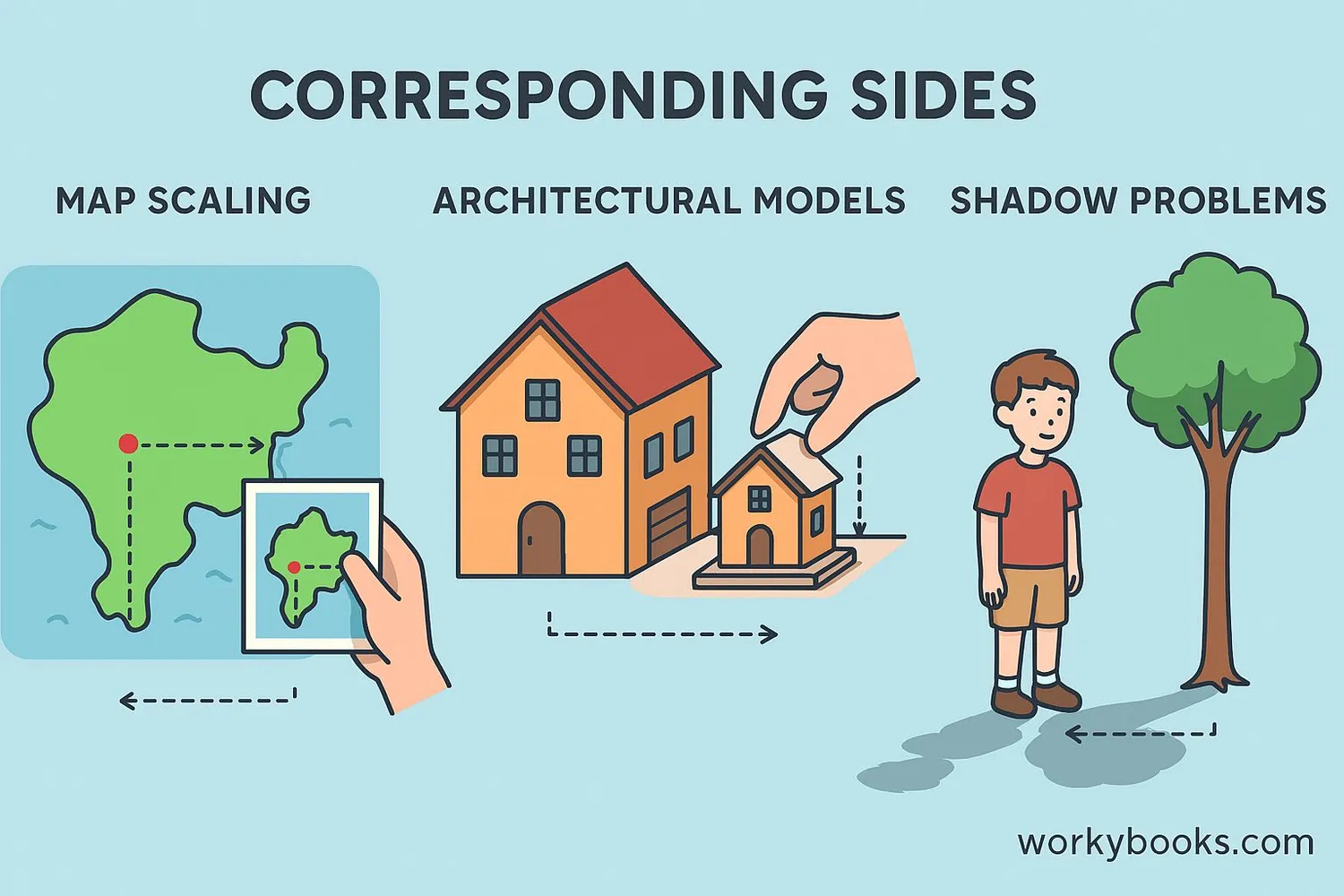
Map Scaling
A map uses a scale of 1cm:5km. If two cities are 8cm apart on the map, the actual distance is 40km. The map distances and real distances are corresponding sides of similar rectangles.
Shadow Problems
A tree casts a 15m shadow while a 2m stick casts a 3m shadow. The triangles formed are similar, so tree height/2 = 15/3 → tree height = 10m.
Architecture
An architect builds a 1:100 scale model of a building. If a window is 2cm wide in the model, it will be 200cm (2m) wide in the actual building.
Practice Tip
Always match angles first to find corresponding sides. Corresponding sides are always opposite corresponding angles.
Practice Quiz
Test your understanding of corresponding sides with this 5-question quiz:
Frequently Asked Questions
Here are answers to common questions about corresponding sides:
Geometry Trivia
Discover interesting facts about geometry and corresponding sides:
Ancient Geometry
The concept of similar triangles was used by ancient Egyptians to measure the height of pyramids. They observed shadows and used proportional relationships between corresponding sides.
Golden Ratio
The golden ratio (approximately 1.618) appears in similar rectangles where the ratio of corresponding sides follows this special proportion, found in art, architecture, and nature.
Space Measurements
Astronomers use similar triangles to measure distances to stars. By observing a star from different positions in Earth's orbit, they create a triangle with Earth's orbit as the base.
Largest Geometric Structure
The Great Pyramid of Giza was built with remarkable geometric precision. Its sides correspond almost perfectly with the cardinal directions (north, south, east, west).





