Cube - Definition, Examples, Quiz, FAQ, Trivia
Learn about cubes: their properties, formulas, and real-world examples
What is a Cube?
A cube is a special three-dimensional shape with all sides of equal length. It's one of the five Platonic solids and is made up of:
• 6 faces - all identical squares
• 12 edges - all of the same length
• 8 vertices - corners where edges meet
Cubes are everywhere in our daily lives! You can find them in dice, sugar cubes, Rubik's cubes, and even buildings.
Since all sides of a cube are equal, it's a very symmetrical and balanced shape.
Key Concept
A cube is a 3D shape with all sides equal and all angles at 90 degrees. Each face is a perfect square.
Properties of a Cube
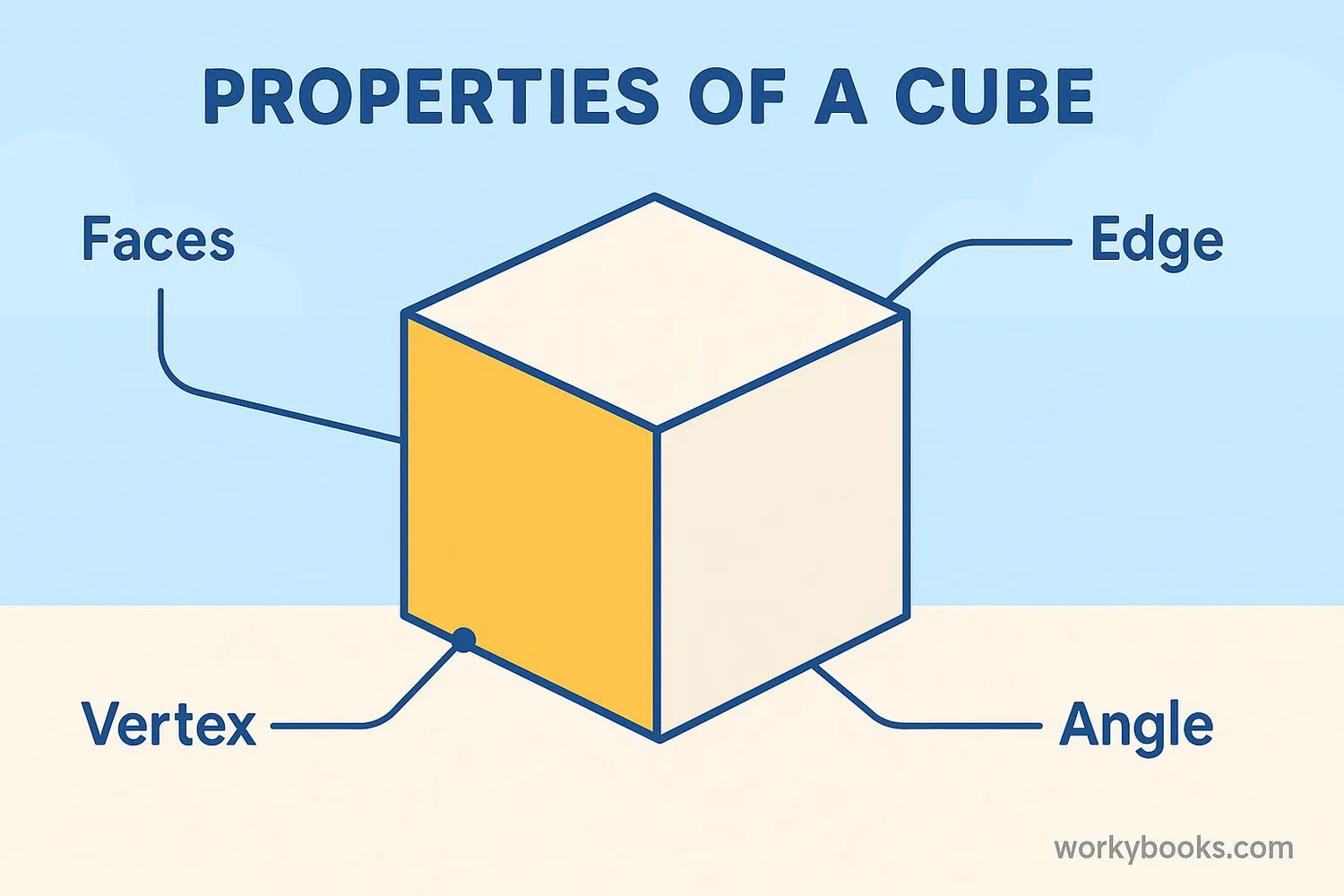
Cubes have special properties that make them unique among 3D shapes. Here are the key features:
Faces
6 identical square faces
Edges
12 edges of equal length
Vertices
8 vertices (corners)
Angles
All angles are right angles (90°)
Remember
In a cube, all faces are squares, and all edges have the same length. This makes it a regular polyhedron.
Volume of a Cube

Volume tells us how much space a 3D shape takes up. For a cube, since all sides are equal, calculating volume is simple:
Volume Formula
Where s is the length of one side of the cube
Example: Find the volume of a cube with side length 4 cm
Step 1: Identify side length → s = 4 cm
Step 2: Apply formula → V = 4 × 4 × 4
Step 3: Calculate → 64 cubic centimeters (cm³)
So a 4 cm cube has a volume of 64 cm³. That means 64 cubes of 1 cm each would fit inside it!
Surface Area of a Cube
Surface area is the total area of all the faces of a 3D shape. Since a cube has 6 identical square faces:
Surface Area Formula
Where s is the length of one side
Example: Find the surface area of a cube with side length 3 cm
Step 1: Area of one face → 3 × 3 = 9 cm²
Step 2: Multiply by 6 faces → 6 × 9 = 54 cm²
So the total surface area is 54 cm². This tells us how much material would be needed to cover the entire cube.
Diagonal of a Cube
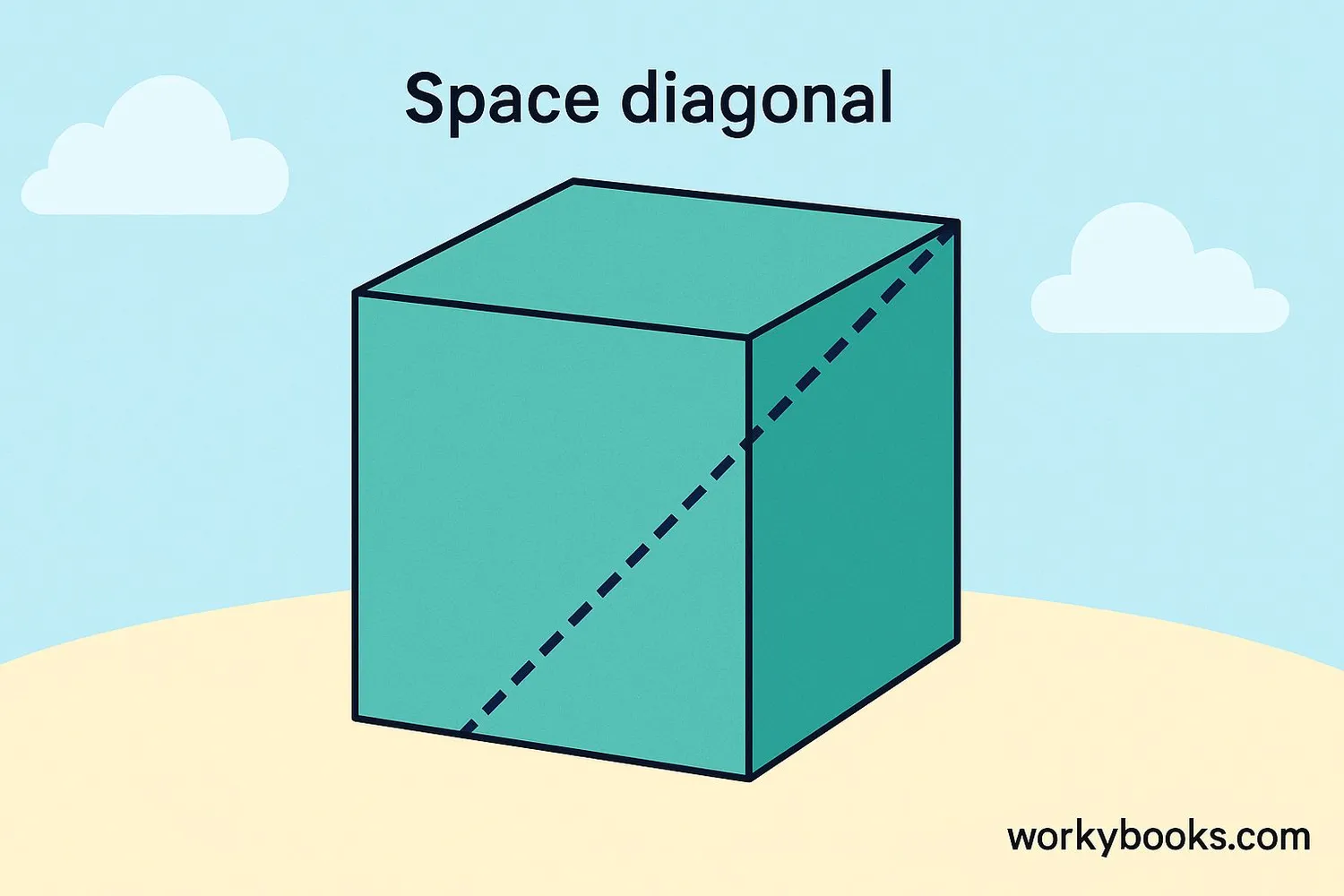
The diagonal of a cube is the longest straight line that can be drawn from one corner to the opposite corner, passing through the inside of the cube. We call this the "space diagonal".
The formula to calculate the diagonal is:
Diagonal Formula
Where s is the side length and √3 is approximately 1.732
Example: Find the diagonal of a cube with side length 5 cm
Step 1: Apply formula → d = 5 × √3
Step 2: Calculate → 5 × 1.732 ≈ 8.66 cm
This diagonal is longer than the face diagonals because it goes through the entire cube.
Cube Knowledge Quiz
Test your understanding of cubes with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cubes:
Math Trivia
Discover interesting facts about cubes and geometry:
Ancient Cubes
The oldest known dice (cubes) date back over 5,000 years and were found in archaeological sites in the Middle East. Ancient civilizations used cubic dice in games of chance.
Crystal Cubes
In nature, the mineral halite (rock salt) forms perfect cubic crystals. The cubic structure results from the arrangement of sodium and chloride ions in a repeating pattern.
Rubik's Cube
The Rubik's Cube, invented in 1974 by Hungarian professor Ernő Rubik, has 43 quintillion (43,252,003,274,489,856,000) possible configurations but only one solution!
Cube Buildings
The world's largest cube-shaped building is the Borg El Arab Tower in Alexandria, Egypt. It's a 145-meter tall skyscraper designed in the shape of a cube.





