Cyclic Quadrilateral - Definition, Examples, Quiz, FAQ, Trivia
Learn about four-sided shapes where all corners touch a single circle
What is a Cyclic Quadrilateral?
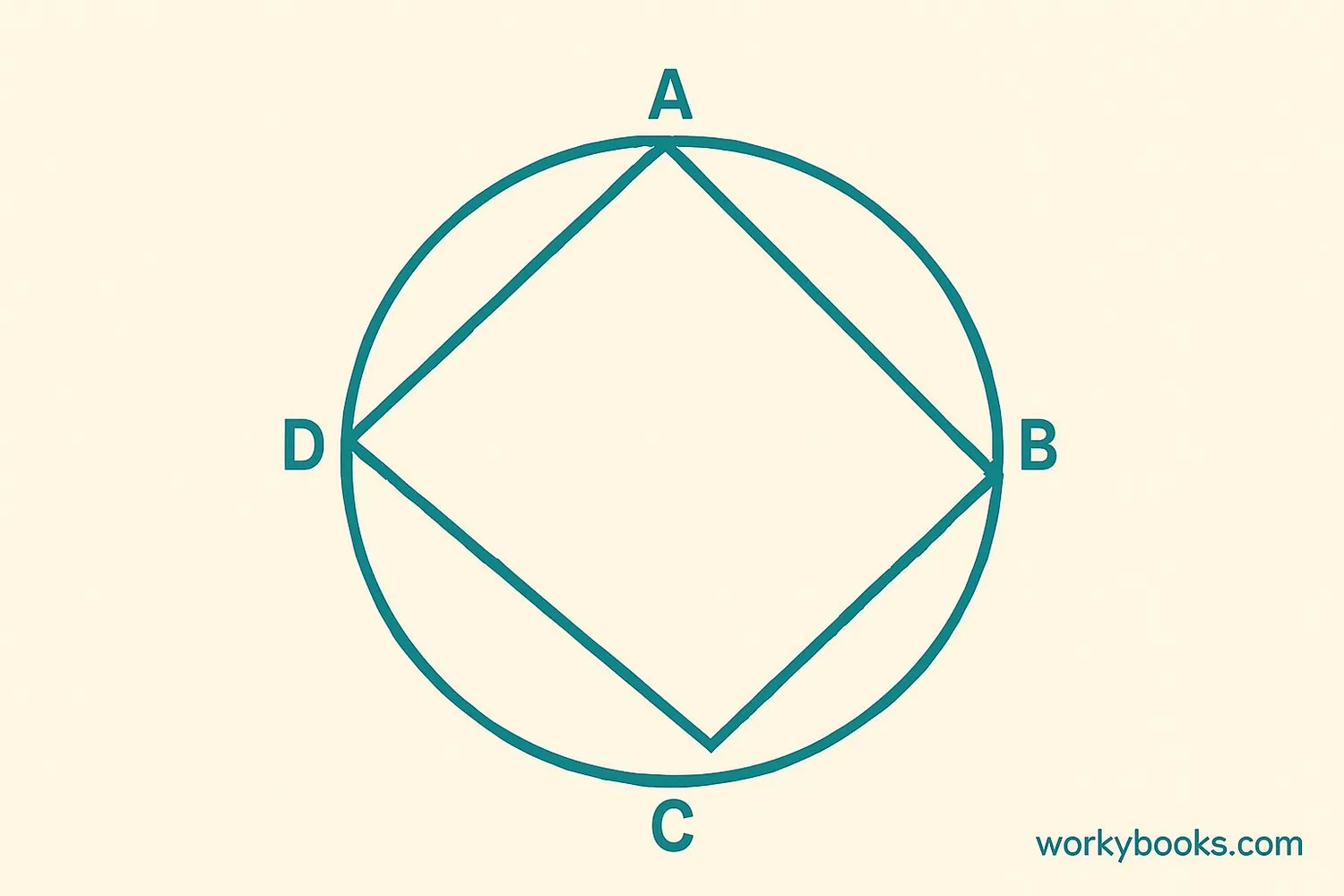
A cyclic quadrilateral is a four-sided shape where all four corners (vertices) lie on a single circle. The word "cyclic" comes from "circle," meaning the quadrilateral is inside a circle with each of its corners touching the circle.
Think of it like this: if you draw a circle and then draw a quadrilateral (a four-sided shape) so that all four corners are touching the circle, you've created a cyclic quadrilateral!
This special relationship creates interesting properties that we'll explore. Many familiar shapes are cyclic quadrilaterals, including squares, rectangles, and isosceles trapezoids.
Key Concept
For a quadrilateral to be cyclic, all four vertices must lie on a single circle.
Properties of Cyclic Quadrilaterals
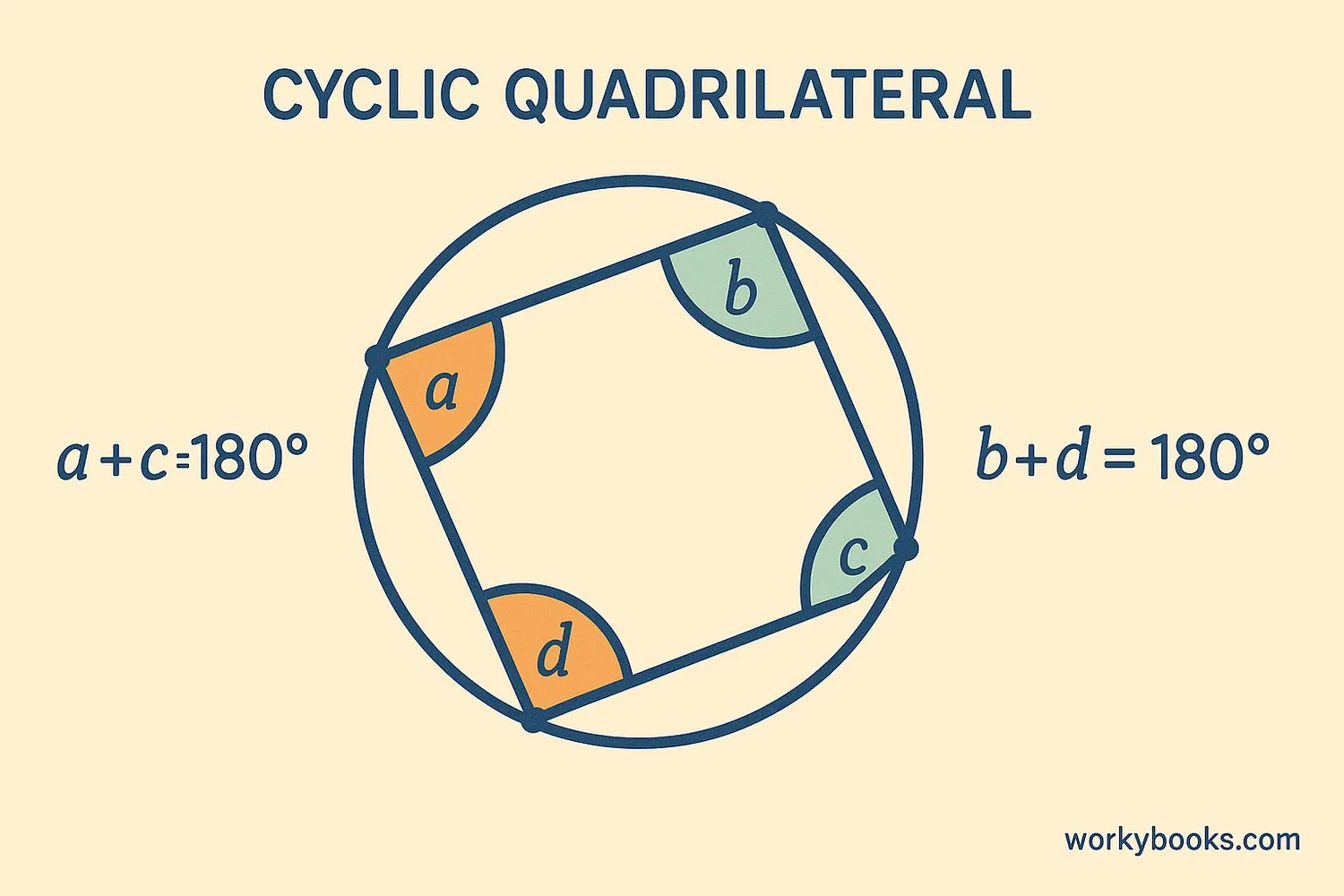
Cyclic quadrilaterals have special properties that make them unique:
-
Opposite angles sum to 180°: The angles at opposite corners add up to 180 degrees. For example, if angle A is 70°, then angle C (opposite) must be 110°.
-
Exterior angle equals opposite interior angle: If you extend one side of the quadrilateral, the angle formed outside equals the opposite interior angle.
-
Perpendicular bisectors meet at one point: The center of the circle is where the perpendicular bisectors of the sides meet.
Remember
The most important property is that opposite angles add to 180°. This is the key way to identify if a quadrilateral is cyclic.
Theorems About Cyclic Quadrilaterals
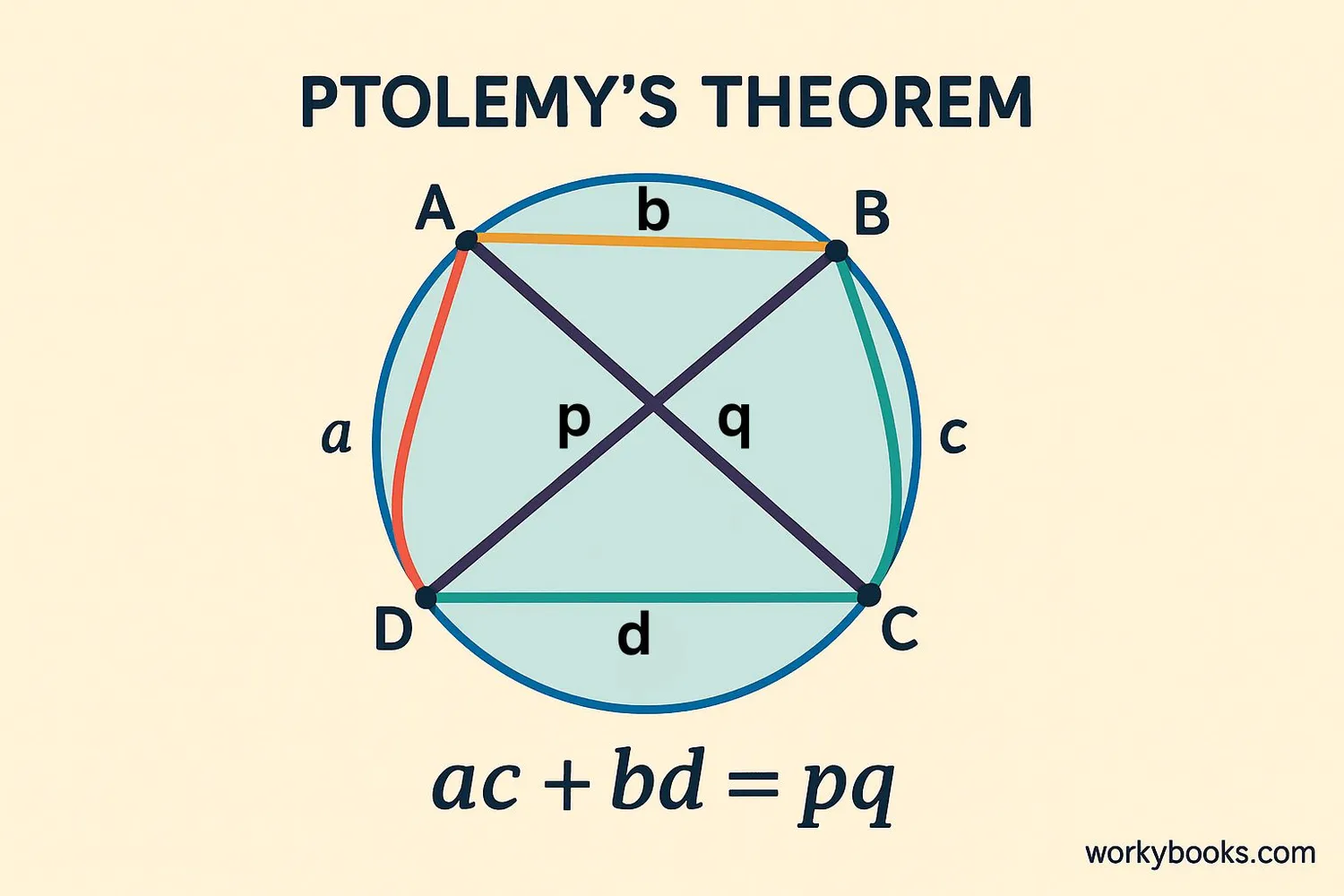
Mathematicians have discovered important rules (theorems) about cyclic quadrilaterals:
Opposite Angles Theorem
The sum of opposite angles in any cyclic quadrilateral is always 180°.
Ptolemy's Theorem
For cyclic quadrilateral ABCD, the product of the diagonals equals the sum of the products of opposite sides.
Theorem Tip
You can use the Opposite Angles Theorem to test if a quadrilateral is cyclic. If opposite angles add to 180°, it must be cyclic!
Examples of Cyclic Quadrilaterals
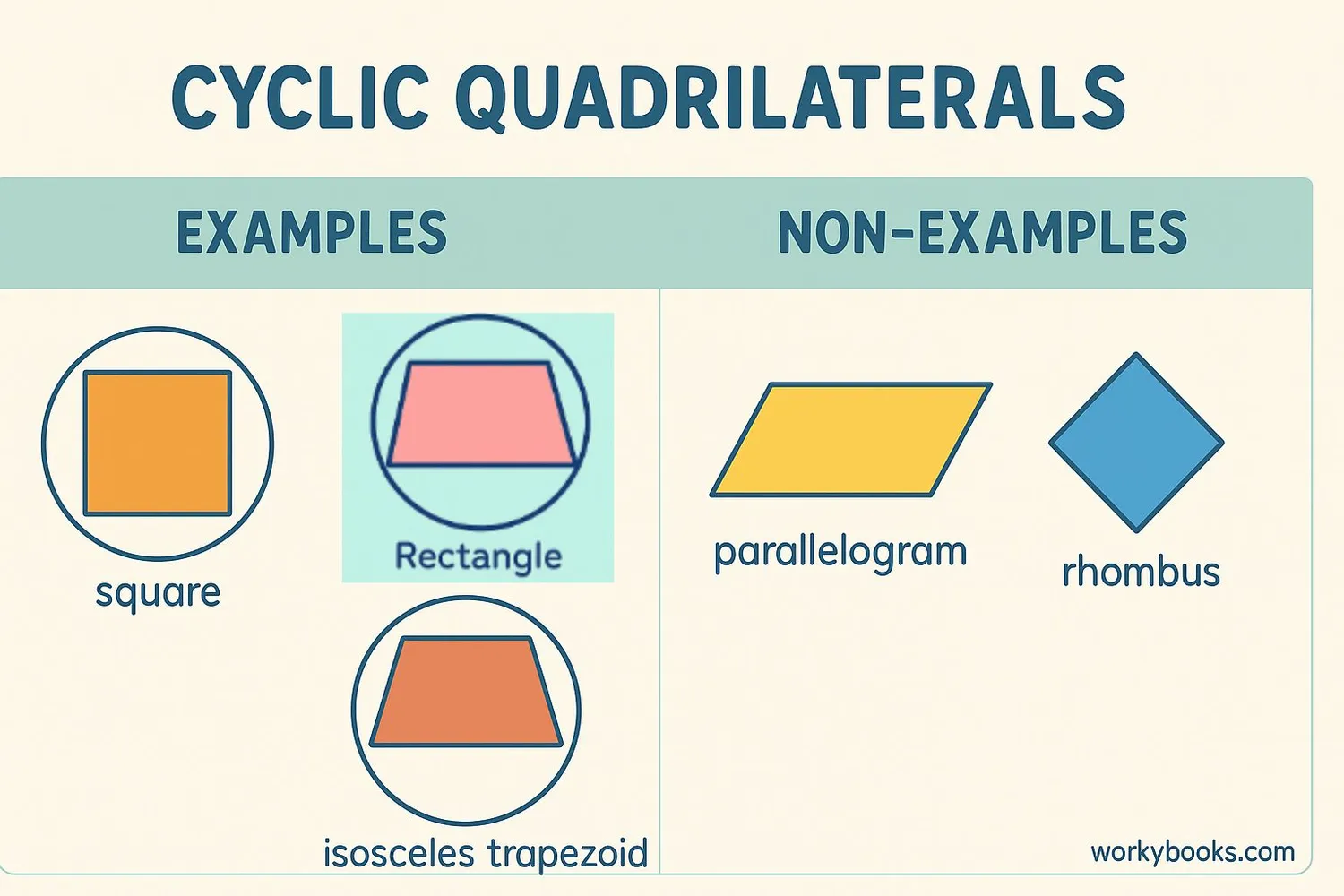
Let's look at some common cyclic quadrilaterals and how to identify them:
Example 1: Square - All squares are cyclic quadrilaterals because all four corners touch a circle.
The circle that passes through all four vertices is called the circumcircle.
Example 2: Rectangle - All rectangles are cyclic quadrilaterals. The opposite angles are both 90°,
and 90° + 90° = 180°, satisfying the opposite angles theorem.
Example 3: Isosceles Trapezoid - A trapezoid with equal base angles is always cyclic.
The non-parallel sides are equal in length.
Non-Example: Parallelogram - Most parallelograms are not cyclic. Only rectangles (a special type of parallelogram) are cyclic.
Non-Example: Rhombus - Rhombi are generally not cyclic unless they are squares (which are special rhombi).
Identification Tip
To check if a quadrilateral is cyclic, measure its opposite angles. If they add to 180°, it's cyclic!
Cyclic Quadrilateral Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about cyclic quadrilaterals:
Geometry Trivia
Discover interesting facts about cyclic quadrilaterals and geometry:
Ancient Discovery
The concept of cyclic quadrilaterals was known to ancient Greek mathematicians as early as 300 BCE. Euclid mentioned properties of cyclic quadrilaterals in his famous work "Elements".
Word Origin
The word "cyclic" comes from the Greek word "kyklos" meaning circle. "Quadrilateral" comes from Latin words "quadri" (four) and "latus" (side).
Real-World Applications
Cyclic quadrilaterals are used in architecture and engineering, especially in designing circular structures like domes and arches where precise angles are important.
Special Cases
All regular polygons with an even number of sides can be divided into cyclic quadrilaterals. For example, a hexagon can be divided into three cyclic quadrilaterals.


