Degrees to Radians - Definition, Examples, Quiz, FAQ, Trivia
Learn to convert between degree and radian angle measurements with easy explanations and practice activities
What is Angle Conversion?
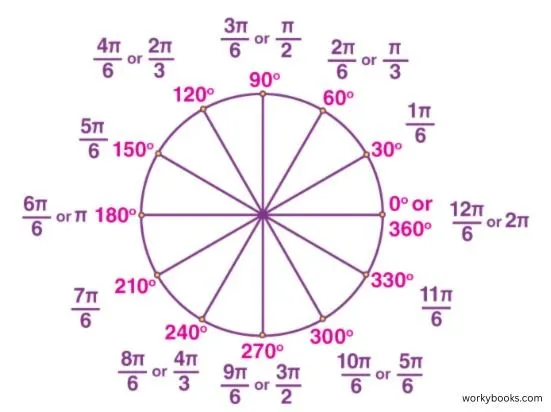
Angle conversion means changing the measurement of an angle from one unit to another. We'll learn how to convert between degrees (commonly used in everyday life) and radians (used in higher mathematics and science).
Why do we need to convert? Degrees are easier for simple measurements, but radians make calculations with circles and trigonometry simpler. Mathematicians and scientists prefer radians for many calculations.
A full circle has 360 degrees. In radians, a full circle is 2π radians (about 6.28). To convert degrees to radians, we multiply the number of degrees by π/180. This relationship helps us solve problems in geometry and physics.
Key Concept
360 degrees = 2π radians. This relationship is the foundation for all degree-to-radian conversions.
How to Convert Degrees to Radians
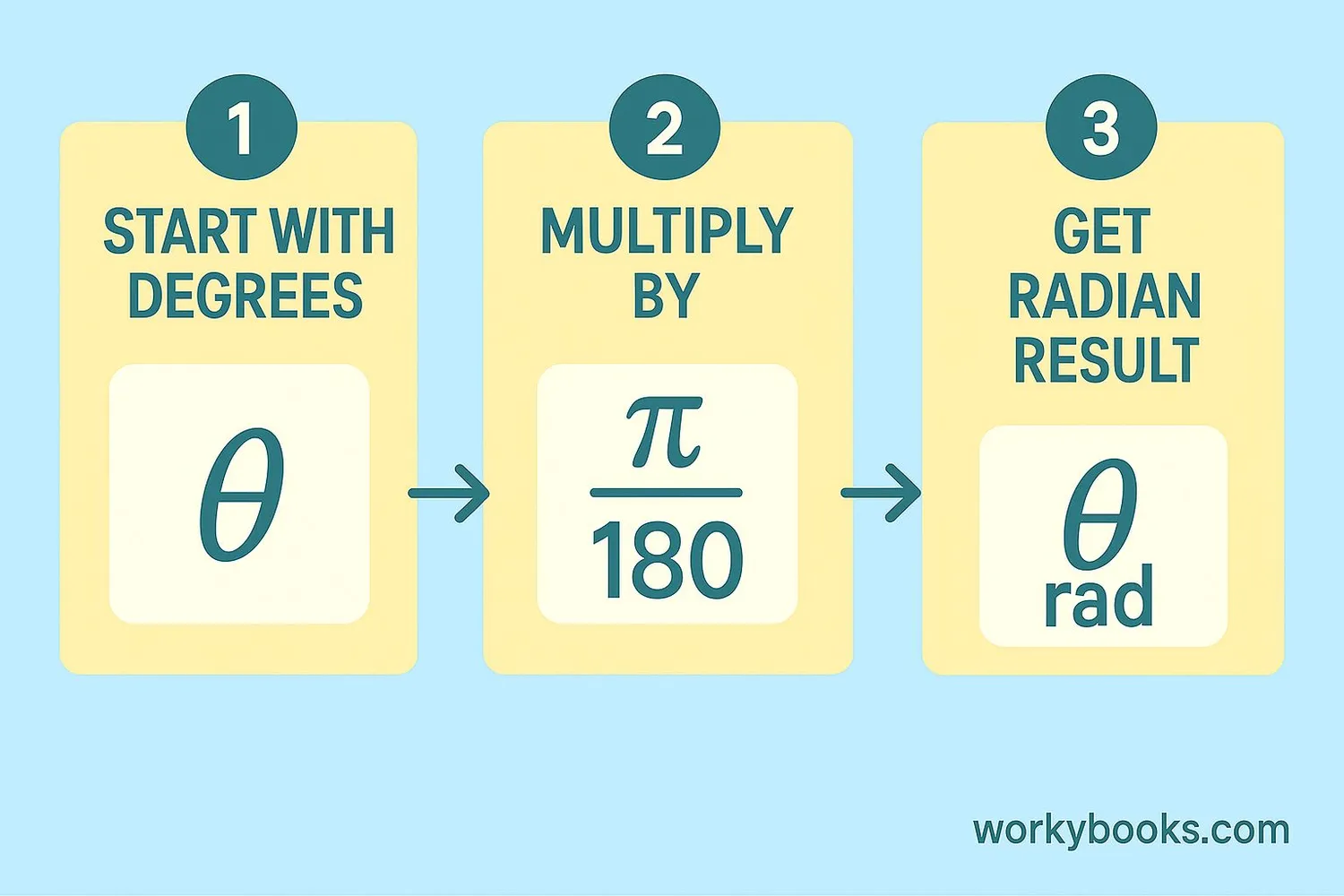
Converting degrees to radians is simple once you remember the conversion formula:
Conversion Formula
To convert any measurement in degrees to radians, multiply the number of degrees by π/180.
Example: Convert 180 degrees to radians
Step 1: Start with the measurement in degrees → 180°
Step 2: Multiply by π/180 → 180 × (π/180)
Step 3: Simplify the result → π radians
So 180 degrees equals π radians. Remember that π is approximately 3.14159.
Remember
When converting degrees to radians, your answer will be in terms of π for common angles like 30°, 45°, 60°, 90°, and 180°.
Degrees to Radians Conversion Charts

Conversion charts help us quickly find equivalent angle measurements without calculating each time. Here's a useful chart for converting degrees to radians:
Degrees to Radians Conversion Chart
| Degrees (°) | Radians (rad) | Radians (in terms of π) |
|---|---|---|
| 0° | 0 | 0 |
| 30° | 0.5236 | π/6 |
| 45° | 0.7854 | π/4 |
| 60° | 1.0472 | π/3 |
| 90° | 1.5708 | π/2 |
| 120° | 2.0944 | 2π/3 |
| 180° | 3.1416 | π |
| 270° | 4.7124 | 3π/2 |
| 360° | 6.2832 | 2π |
Chart Tip
Notice how 180° equals π radians? You can use this to convert any angle: radians = (degrees × π)/180
Real-World Examples
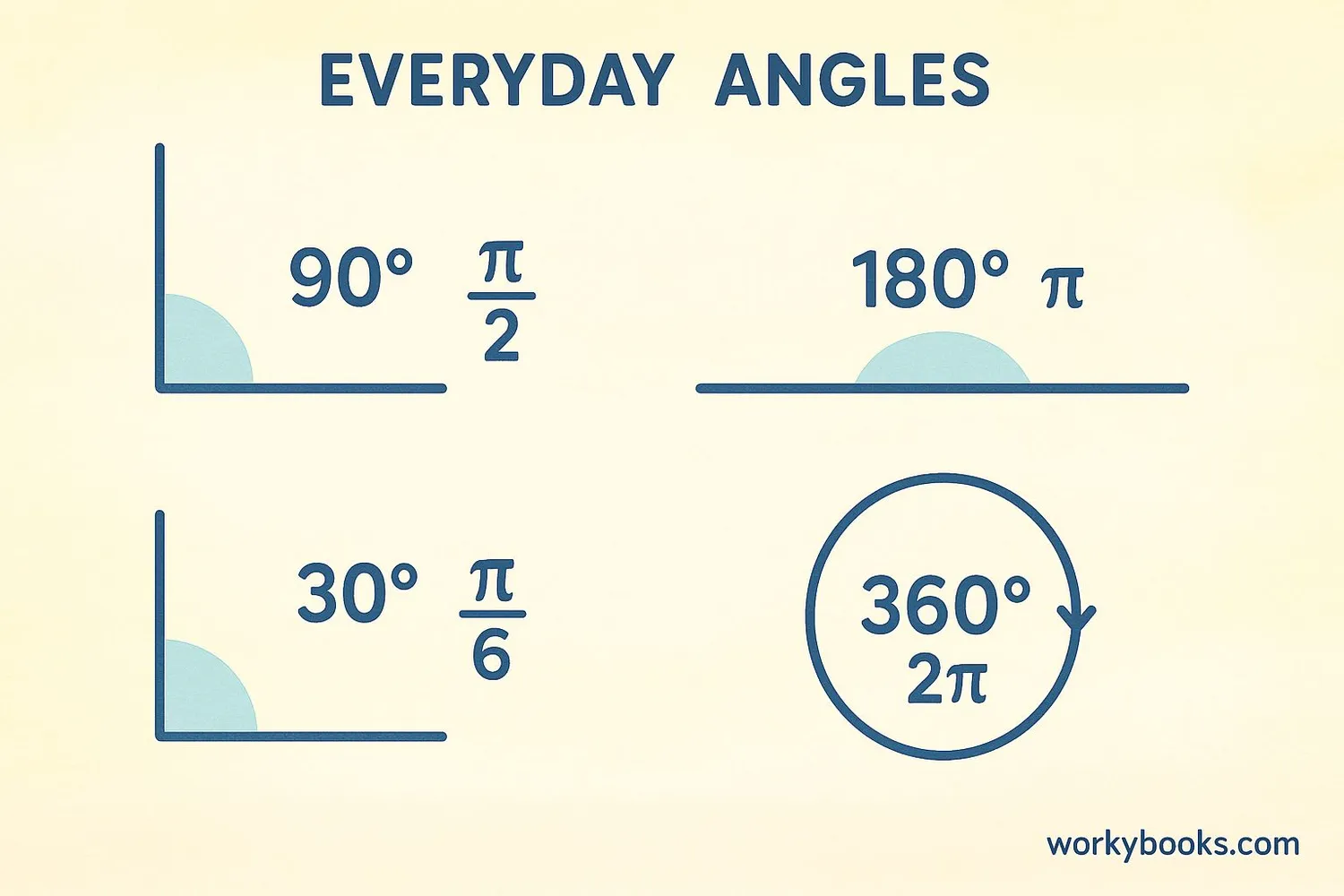
Let's practice conversion with some real-world examples:
Example 1: A clock shows 3:00. The angle between the hour and minute hands is 90°. What is this angle in radians?
Solution: 90 × (π/180) = π/2 radians
Example 2: A skateboard ramp forms a 30° angle with the ground. Convert this to radians.
Solution: 30 × (π/180) = π/6 radians
Example 3: A pizza slice has a central angle of 45°. What is this angle in radians?
Solution: 45 × (π/180) = π/4 radians
Example 4: A protractor shows an angle of 120°. Convert this to radians.
Solution: 120 × (π/180) = 2π/3 radians
Practice converting angles you see around you - corners of objects, angles in shapes, or positions on a clock!
Conversion Tip
To convert radians back to degrees, multiply by 180/π instead of multiplying by π/180.
Conversion Practice Quiz
Test your conversion skills with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about degrees and radians conversion:
Angle Measurement Trivia
Discover interesting facts about angles and measurement systems:
Origin of Degrees
The degree system dates back to ancient Babylonians around 4000 years ago. They divided a circle into 360 parts because 360 has many divisors and it matched their base-60 number system.
Radian Advantage
Radians are called "natural" units because when angles are measured in radians, the derivative of sin(x) is cos(x), making calculus operations simpler. This relationship doesn't hold for degrees.
Space Exploration
NASA uses radians for all spacecraft navigation and trajectory calculations because they provide more precise measurements for the vast distances and angles involved in space travel.
Most Important Angle
The right angle (90°) is considered the most important angle in architecture and construction. The pyramids of Egypt and modern skyscrapers all rely on precise right angles for stability.





