Diameter Formula - Definition, Examples, Quiz, FAQ, Trivia
Learn about circles, diameter, radius, and how to calculate them with easy explanations and practice activities
What is Diameter?
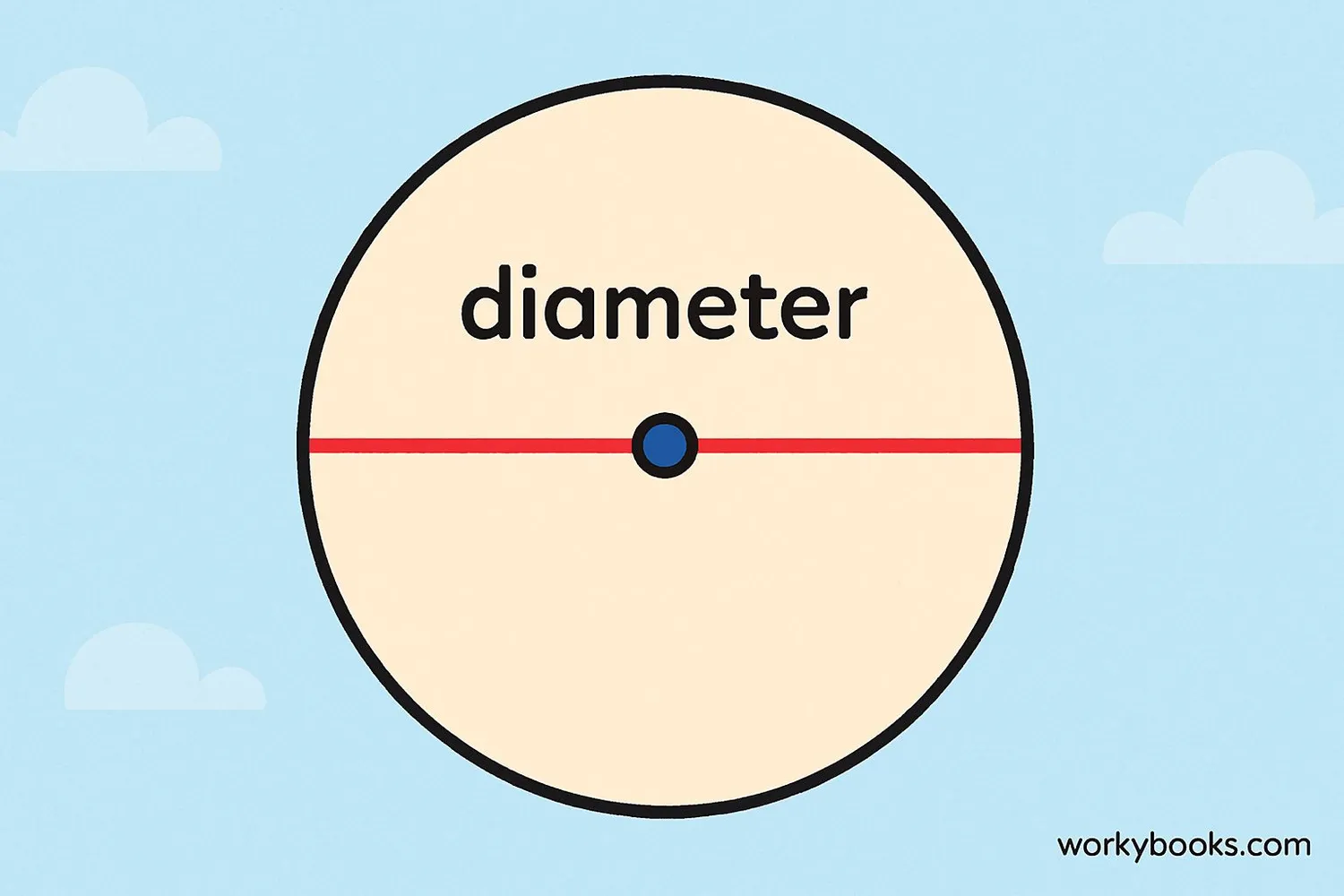
The diameter of a circle is a straight line that passes from one side of the circle to the other side through its center point. It is the longest distance you can measure across any circle.
Diameter is important because it helps us understand the size of a circle. When you know the diameter, you can calculate many other properties of the circle, like its circumference (the distance around the circle) and area (the space inside the circle).
The diameter is always twice as long as the radius, which is the distance from the center to the edge of the circle.
Key Concept
The diameter is the longest chord in a circle and always passes through the center point.
Diameter Formula
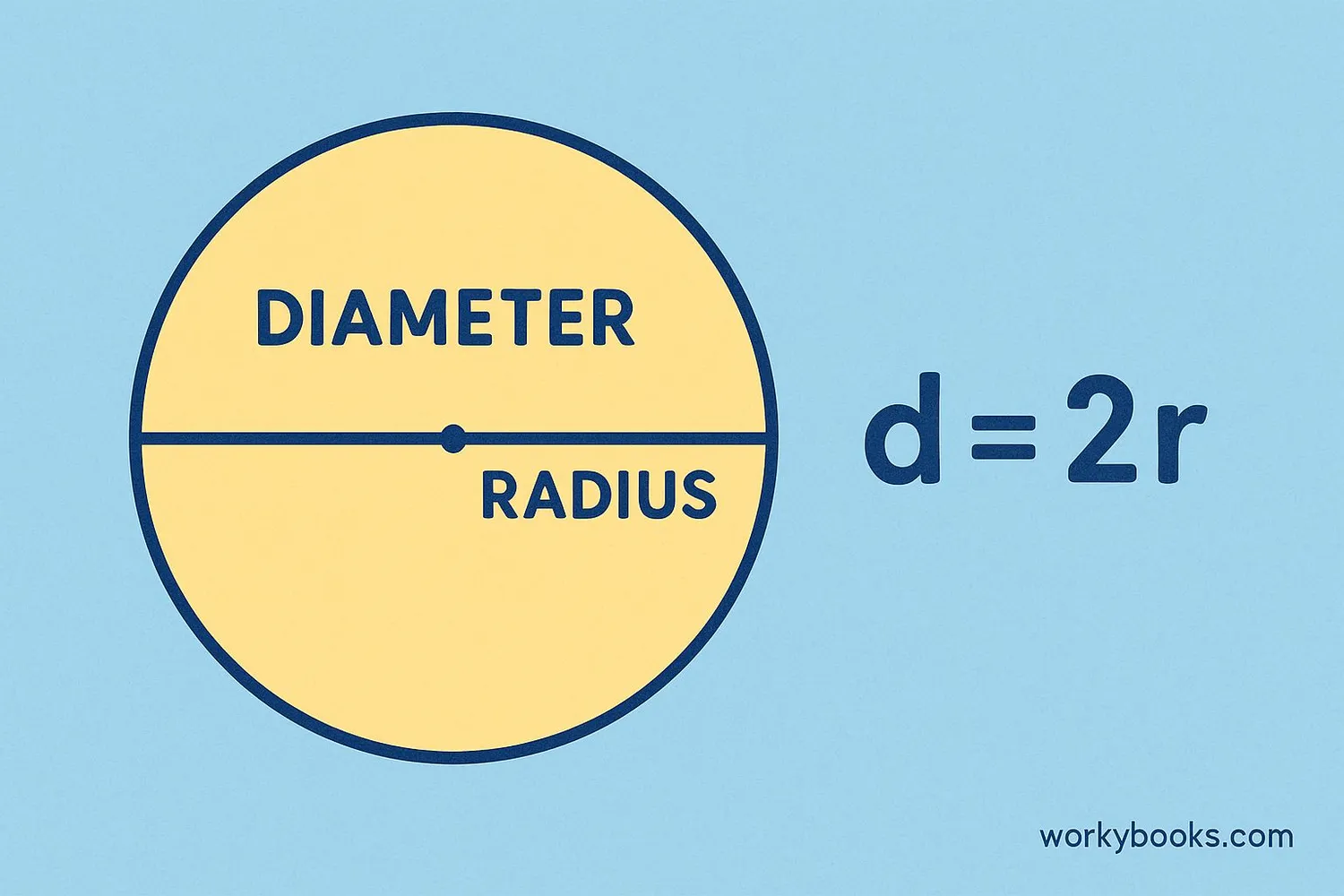
The diameter formula is simple and easy to remember. It relates the diameter to the radius:
Diameter Formula
Where d is the diameter and r is the radius of the circle.
Example: If a circle has a radius of 5 cm, what is its diameter?
Step 1: Identify the radius → r = 5 cm
Step 2: Apply the formula → d = 2 × 5 cm
Step 3: Calculate → d = 10 cm
So the diameter is 10 centimeters.
Remember
Diameter is always twice the radius, so if you know one, you can always find the other!
Relationship with Radius and Circumference
Diameter has important relationships with other circle measurements:
Radius: As we've learned, diameter = 2 × radius. This also means that radius = diameter ÷ 2.
Circumference: The circumference (C) is the distance around the circle. It's related to the diameter through the mathematical constant π (pi, approximately 3.14). The formula is:
Circumference Formula
Where C is the circumference and d is the diameter.
Step 1: Identify the diameter → d = 10 cm
Step 2: Apply the formula → C = π × 10 cm
Step 3: Calculate → C ≈ 3.14 × 10 cm = 31.4 cm
So the circumference is approximately 31.4 centimeters.
Pi Fact
π (pi) is a special number in mathematics that represents the ratio of a circle's circumference to its diameter. It's approximately 3.14159 but has an infinite number of digits!
Examples
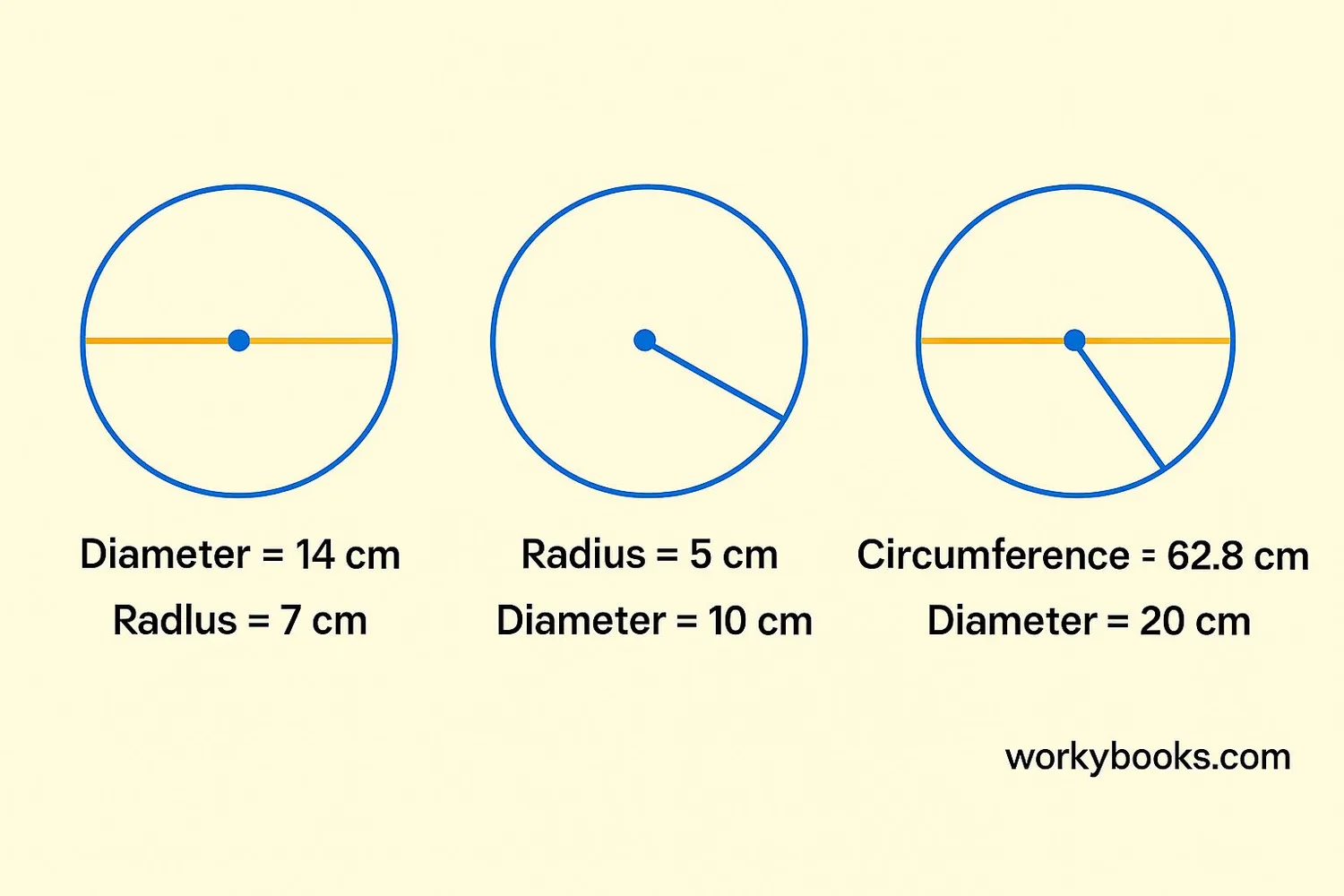
Let's practice with some real-world examples:
Example 1: A bicycle wheel has a radius of 35 cm. What is its diameter?
Solution: d = 2 × r = 2 × 35 cm = 70 cm
Example 2: A circular table has a diameter of 120 cm. What is its radius?
Solution: r = d ÷ 2 = 120 cm ÷ 2 = 60 cm
Example 3: A circular pond has a circumference of 31.4 meters. What is its diameter?
Solution: C = π × d → 31.4 = 3.14 × d → d = 31.4 ÷ 3.14 = 10 meters
Example 4: A pizza has a diameter of 40 cm. What is its radius?
Solution: r = d ÷ 2 = 40 cm ÷ 2 = 20 cm
Practice finding diameters in everyday objects - plates, coins, wheels, and clocks!
Remember
When solving problems, always note whether you're given the radius or diameter. This will determine which formula to use.
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about diameter and circles:
Circle Trivia
Discover interesting facts about circles and diameter:
Ancient Circles
The earliest known use of circles dates back to prehistoric times. Stonehenge, built around 3000 BC, features circular arrangements of massive stones.
Perfect Circles in Nature
While perfect circles are rare in nature, some come very close. Bubbles form nearly perfect spheres (3D circles) because surface tension pulls them into the shape with the smallest surface area.
Circles in Space
Planets and stars appear circular because gravity pulls matter equally toward a central point. This creates the most stable shape - a sphere, which is a 3D circle.
Largest Circle
The largest circle ever drawn by hand has a diameter of 1,401 feet (427 meters). It was created in the desert of Nevada in 2016.





