Distance Between Point and Plane - Definition, Examples, Quiz, FAQ, Trivia
Learn to calculate the shortest distance in 3D space with easy explanations and practice activities
What is Distance Between Point and Plane?

In 3D geometry, a plane is a flat, two-dimensional surface that extends infinitely in all directions. A point is a specific location in space. The distance between a point and a plane is the length of the shortest path connecting them, which is always a straight line that's perpendicular to the plane.
Why is this important? This concept helps us solve real-world problems like finding the shortest distance from a drone to the ground, determining how close a satellite is to Earth's orbital plane, or calculating distances in architecture and engineering.
The key to understanding this distance is the normal vector - an arrow perpendicular to the plane. The distance calculation uses this normal vector to find the shortest path.
Key Concept
The shortest distance between a point and a plane is always perpendicular to the plane. This perpendicular line is called the normal to the plane.
How to Calculate the Distance

To calculate the distance between a point and a plane, we use a special formula. First, we need to know:
- The equation of the plane: ax + by + cz + d = 0
- The coordinates of the point: (x₀, y₀, z₀)
Distance Formula
This formula gives us the shortest distance from point (x₀, y₀, z₀) to the plane ax + by + cz + d = 0
- The numerator |ax₀ + by₀ + cz₀ + d| is the absolute value of the plane equation with the point's coordinates plugged in
- The denominator √(a² + b² + c²) is the length of the normal vector to the plane
This formula works because it calculates how far the point is from the plane along the perpendicular direction.
Remember
The values a, b, and c in the plane equation form the normal vector (a, b, c) that's perpendicular to the plane.
Step-by-Step Examples
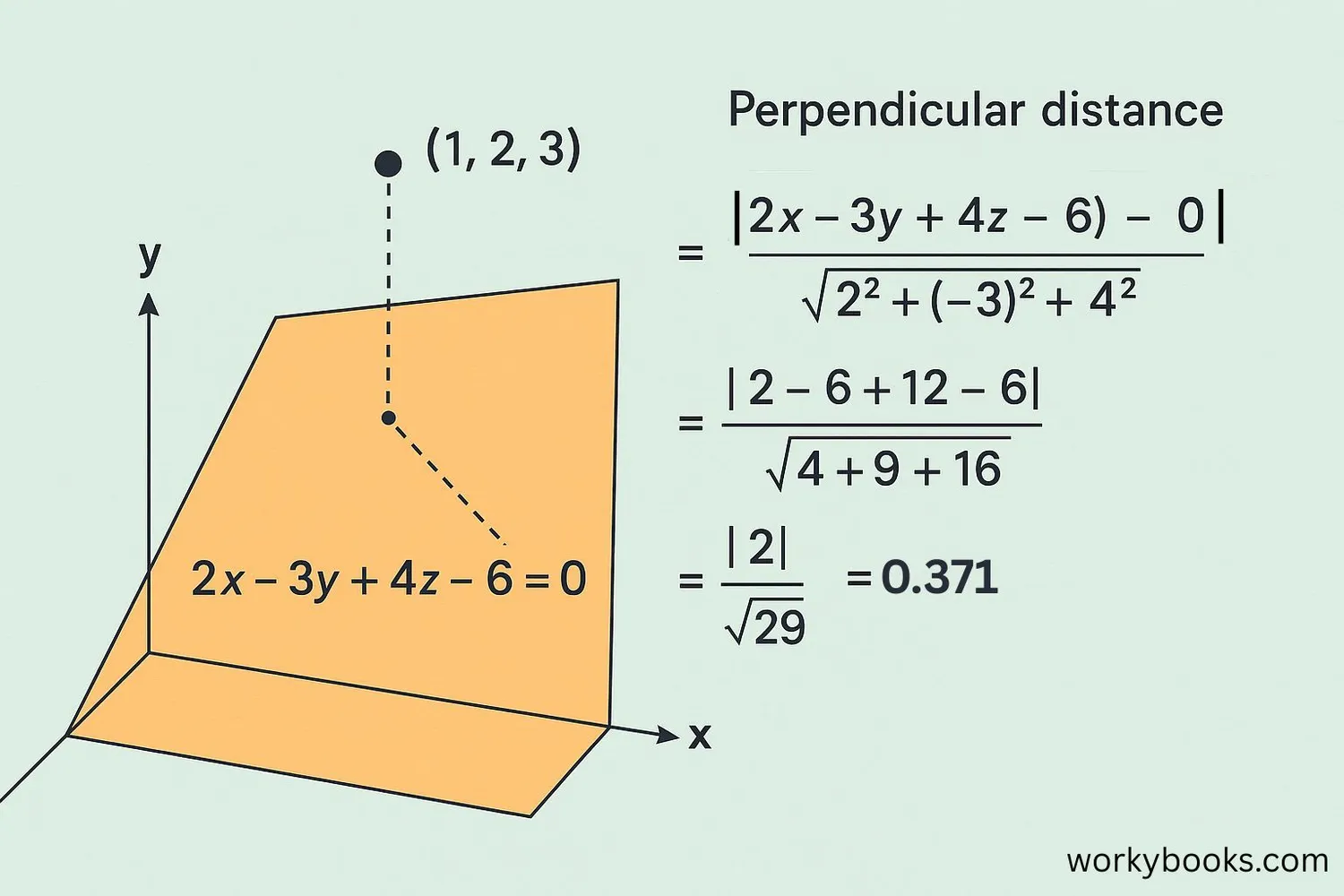
Let's work through an example together to see how the formula works:
Example 1: Basic Calculation
Plane: 2x - 3y + 4z - 6 = 0
Point: (1, 2, 3)
Step 1: Identify a, b, c, d from the plane equation
a = 2, b = -3, c = 4, d = -6
Step 2: Plug the point into the numerator: |2(1) + (-3)(2) + 4(3) - 6|
= |2 - 6 + 12 - 6| = |2| = 2
Step 3: Calculate the denominator: √(2² + (-3)² + 4²)
= √(4 + 9 + 16) = √29 ≈ 5.385
Step 4: Divide: 2 / 5.385 ≈ 0.371
Answer: The distance is approximately 0.371 units
Example 2: Distance to Coordinate Plane
Plane: The xy-plane (z = 0)
Point: (4, -2, 5)
Step 1: Write the plane equation: 0x + 0y + 1z = 0 (so z = 0)
a = 0, b = 0, c = 1, d = 0
Step 2: Numerator: |0(4) + 0(-2) + 1(5) + 0| = |5| = 5
Step 3: Denominator: √(0² + 0² + 1²) = √1 = 1
Step 4: Distance = 5/1 = 5 units
This makes sense because the point is 5 units above the xy-plane!
Calculation Tip
When the plane is one of the coordinate planes (xy, xz, or yz), the distance is simply the absolute value of the coordinate not in that plane.
Distance Calculation Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about distance to a plane:
Geometry Trivia
Discover interesting facts about geometry and measurement:
Ancient Geometry
The concept of planes and points dates back to ancient Greek mathematicians like Euclid (300 BC), who wrote "Elements" - the foundational textbook for geometry that was used for over 2,000 years!
Space Navigation
NASA uses the distance to plane concept for spacecraft navigation. When a spacecraft enters orbit, engineers calculate its distance from the orbital plane to ensure it stays on the correct path around Earth or other planets.
Robotics Applications
Robotic arms in factories use point-to-plane distance calculations to precisely position tools and components. This ensures accurate manufacturing of everything from cars to smartphones.
3D Graphics
Video games and CGI movies use distance to plane calculations millions of times per second to create realistic 3D environments. This determines what objects are visible and how light interacts with surfaces.





