Distance Between Two Points - Definition, Examples, Quiz, FAQ, Trivia
Learn how to calculate distances on number lines and coordinate planes with simple explanations and activities
What is Distance Between Points?
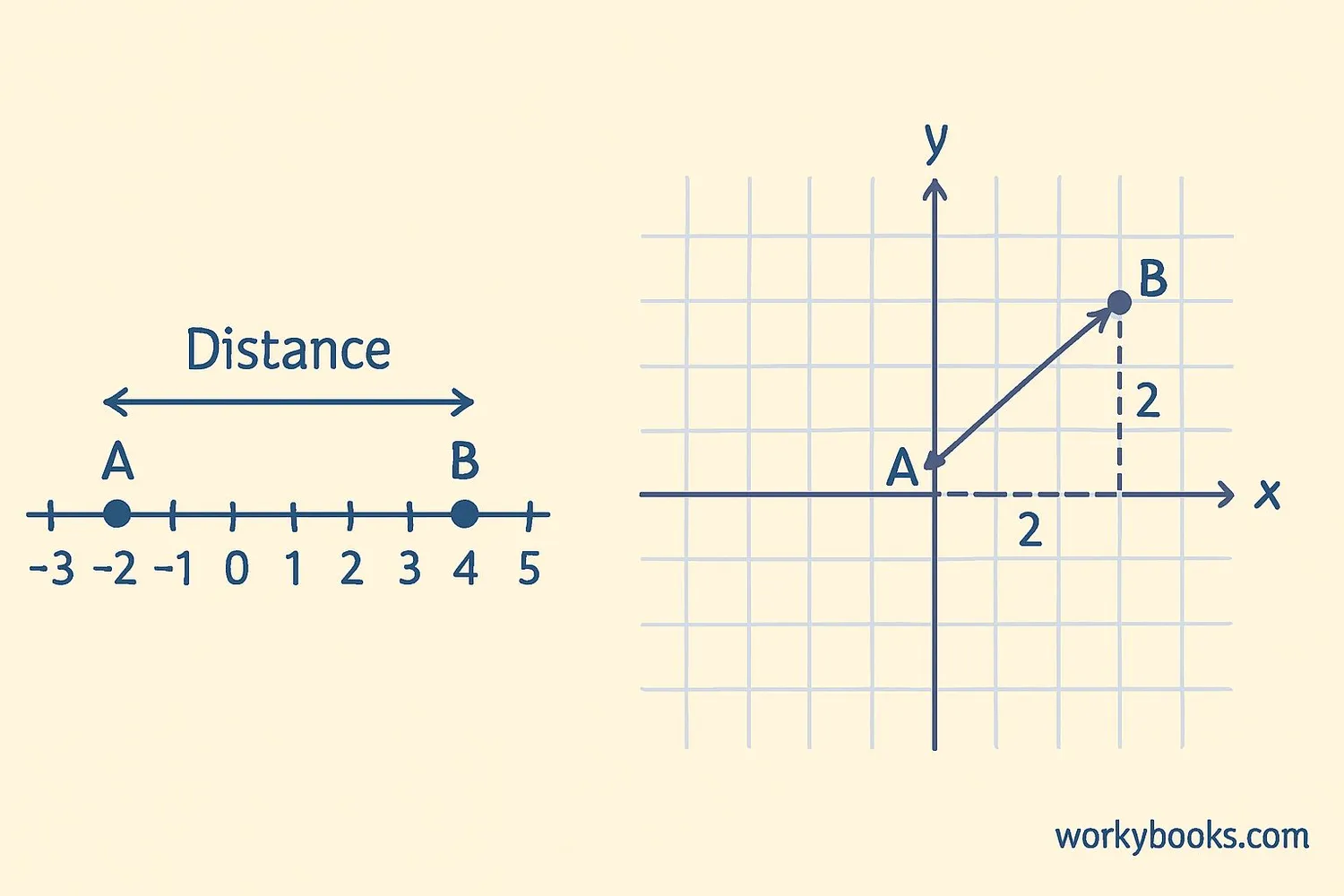
The distance between two points is the length of the straight line connecting them. It's the shortest path between them, like how a bird would fly directly from one place to another.
We measure distance in units like centimeters, meters, or inches. In math, we calculate distance using coordinates on a number line or coordinate plane.
Understanding distance helps us solve real-world problems like:
- How far is your home from school?
- How long is a diagonal line in a rectangle?
- What's the shortest path between two locations?
Key Concept
Distance is always positive. It doesn't matter which point you start from - the distance between A and B is the same as between B and A.
Distance on a Number Line
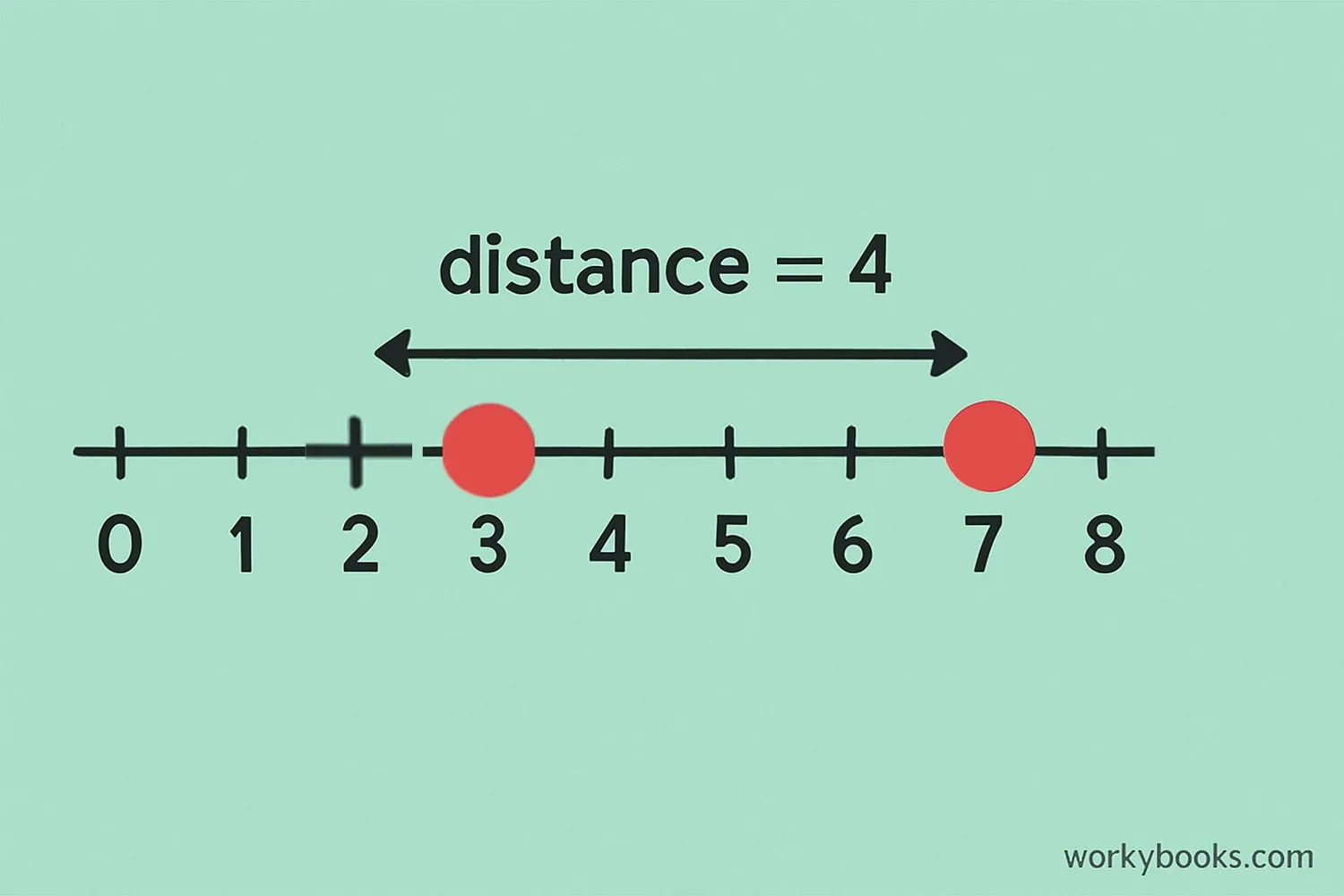
A number line helps us find distances in one dimension. Here's how to calculate distance:
Number Line Distance Formula
Take the absolute value of the difference between the two points
Step 1: Identify points: x₁ = 3, x₂ = 7
Step 2: Calculate difference: 7 - 3 = 4
Step 3: Apply absolute value: |4| = 4
The distance is 4 units. Notice that |3 - 7| = |-4| = 4 also gives the same result!
Remember
Absolute value (| |) makes sure distance is always positive. Distance can never be negative!
Distance in the Coordinate Plane
For points in two dimensions, we use the distance formula based on the Pythagorean Theorem:
Distance Formula
Where (x₁, y₁) and (x₂, y₂) are the coordinates of two points
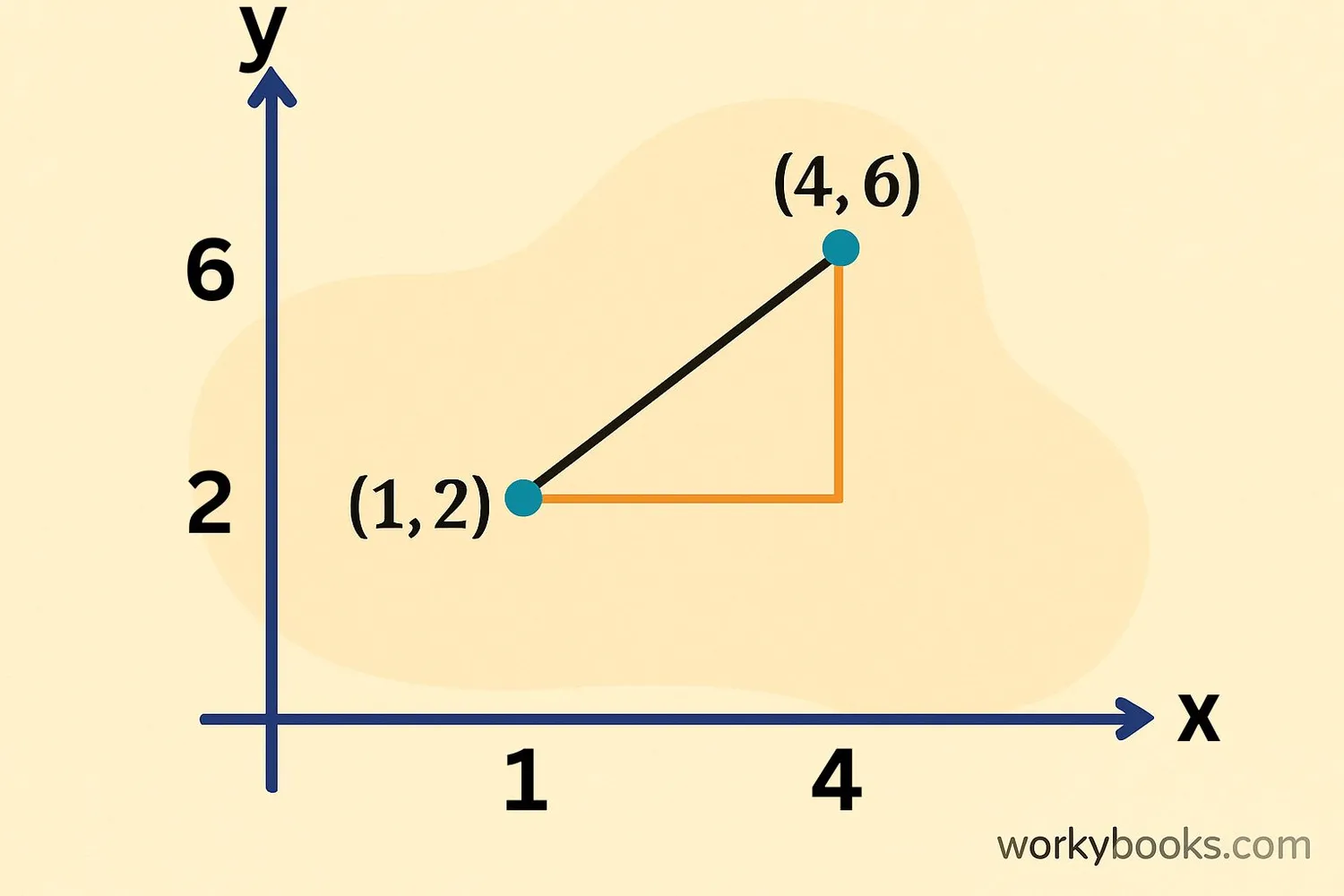
Example: Find the distance between (1, 2) and (4, 6)
Step 1: Identify coordinates: (x₁, y₁) = (1, 2), (x₂, y₂) = (4, 6)
Step 2: Calculate differences:
Δx = 4 - 1 = 3
Δy = 6 - 2 = 4
Step 3: Square the differences: 3² = 9, 4² = 16
Step 4: Sum the squares: 9 + 16 = 25
Step 5: Take square root: √25 = 5
The distance is 5 units. Notice 3-4-5 is a Pythagorean triple!
Real-World Examples

Let's practice with some examples:
Example 1: On a number line, point A is at -3 and point B is at 5. What's the distance?
Solution: |5 - (-3)| = |8| = 8 units
Example 2: Find the distance between (0, 0) and (3, 4)
Solution: √[(3-0)² + (4-0)²] = √[9 + 16] = √25 = 5 units
Example 3: A football field is 100 yards long and 50 yards wide. What's the distance between opposite corners?
Solution: √[100² + 50²] = √[10,000 + 2,500] = √12,500 ≈ 111.8 yards
Example 4: On a map, your home is at (2, 4) and school is at (5, 1). How far is school from home?
Solution: √[(5-2)² + (1-4)²] = √[3² + (-3)²] = √[9 + 9] = √18 ≈ 4.24 units
Distance Tip
Always label your points as (x₁, y₁) and (x₂, y₂) before using the distance formula to avoid mistakes.
Distance Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about distance between points:
Math Trivia
Discover interesting facts about distance and measurement:
Ancient Measurement
The earliest known standardized measurement of distance was the Egyptian cubit around 3000 BC, based on the length of the forearm from the elbow to the tip of the middle finger.
Earth's Circumference
Eratosthenes calculated Earth's circumference around 240 BC by measuring the distance between two Egyptian cities and the angle of the sun's shadows. His estimate was remarkably close to modern measurements.
Cosmic Distances
The distance to our nearest star (Proxima Centauri) is about 40 trillion kilometers. Space scientists use light-years to measure these vast distances - one light-year is about 9.46 trillion kilometers.
Manhattan Distance
In grid-based navigation, "Manhattan distance" measures distance as if you could only move horizontally and vertically (like city blocks). This is different from straight-line distance and is useful in computer science.





