Division by Zero - Definition, Examples, Quiz, FAQ, Trivia
Learn why division by zero is undefined with easy explanations, examples, and interactive activities
What is Division by Zero?

Division by zero means trying to divide any number by zero. In mathematics, this operation is considered undefined, which means it doesn't have a meaningful answer.
Think of division as sharing equally. If you have 12 cookies and want to share them with 4 friends, each gets 3 cookies (12 ÷ 4 = 3). But if you try to share 12 cookies with zero friends (12 ÷ 0), how many cookies does each "friend" get? This question doesn't make sense because there's no one to share with!
Division by zero breaks the rules of mathematics because it leads to impossible situations and contradictions. That's why mathematicians say division by zero is undefined.
Key Concept
Division by zero is undefined in mathematics. No number can be divided by zero and produce a meaningful result.
Why is Division by Zero Undefined?
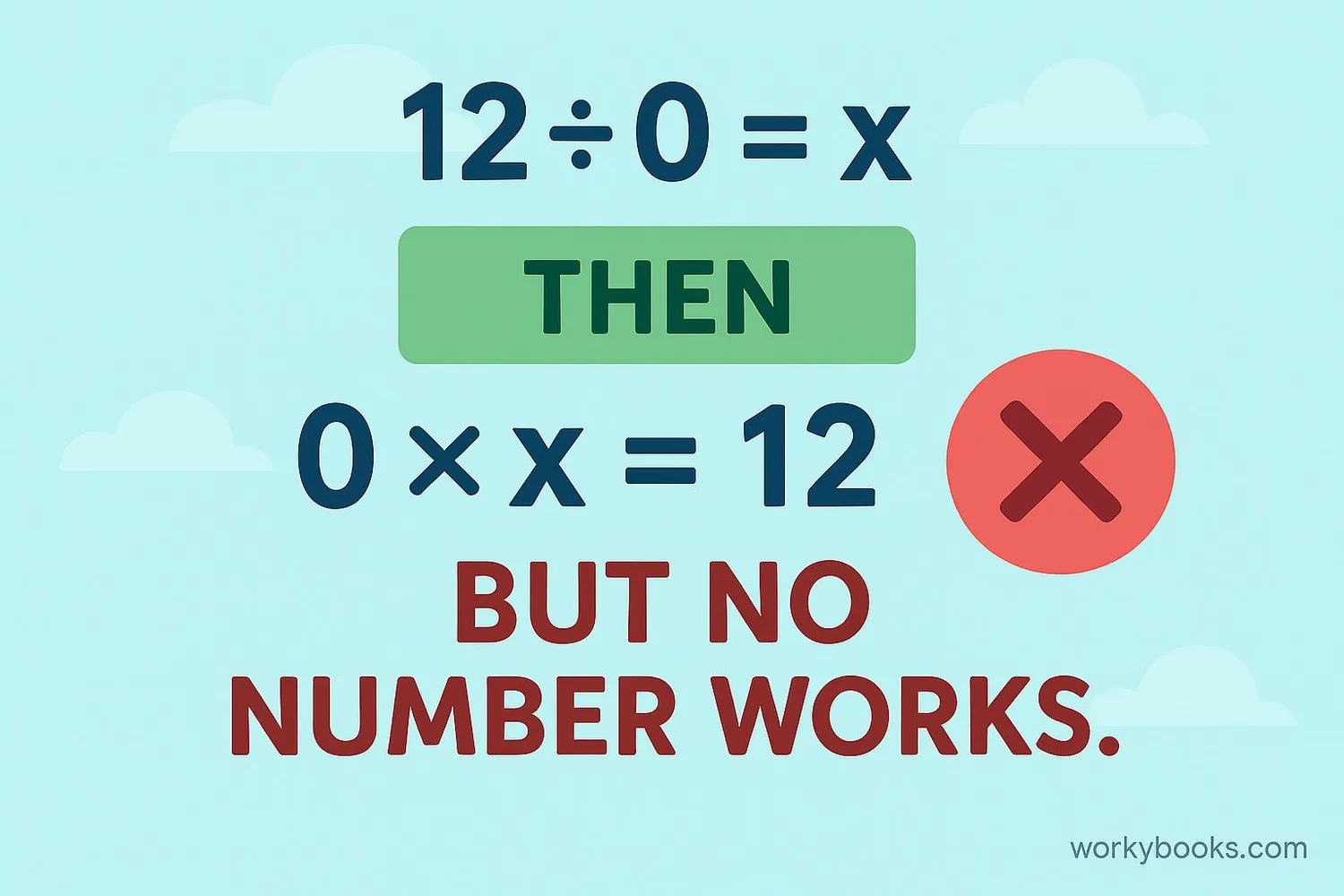
Division is the inverse operation of multiplication. This means that if a ÷ b = c, then b × c should equal a.
Let's test this with division by zero:
Mathematical Proof
If 12 ÷ 0 = x, then 0 × x should equal 12
This creates a contradiction, so no such x exists
Even calculators and computers are programmed to show an error when you try to divide by zero because it's mathematically impossible!
Remember
Division by zero is undefined because no number multiplied by zero can give a non-zero result.
Division by Zero Fallacies
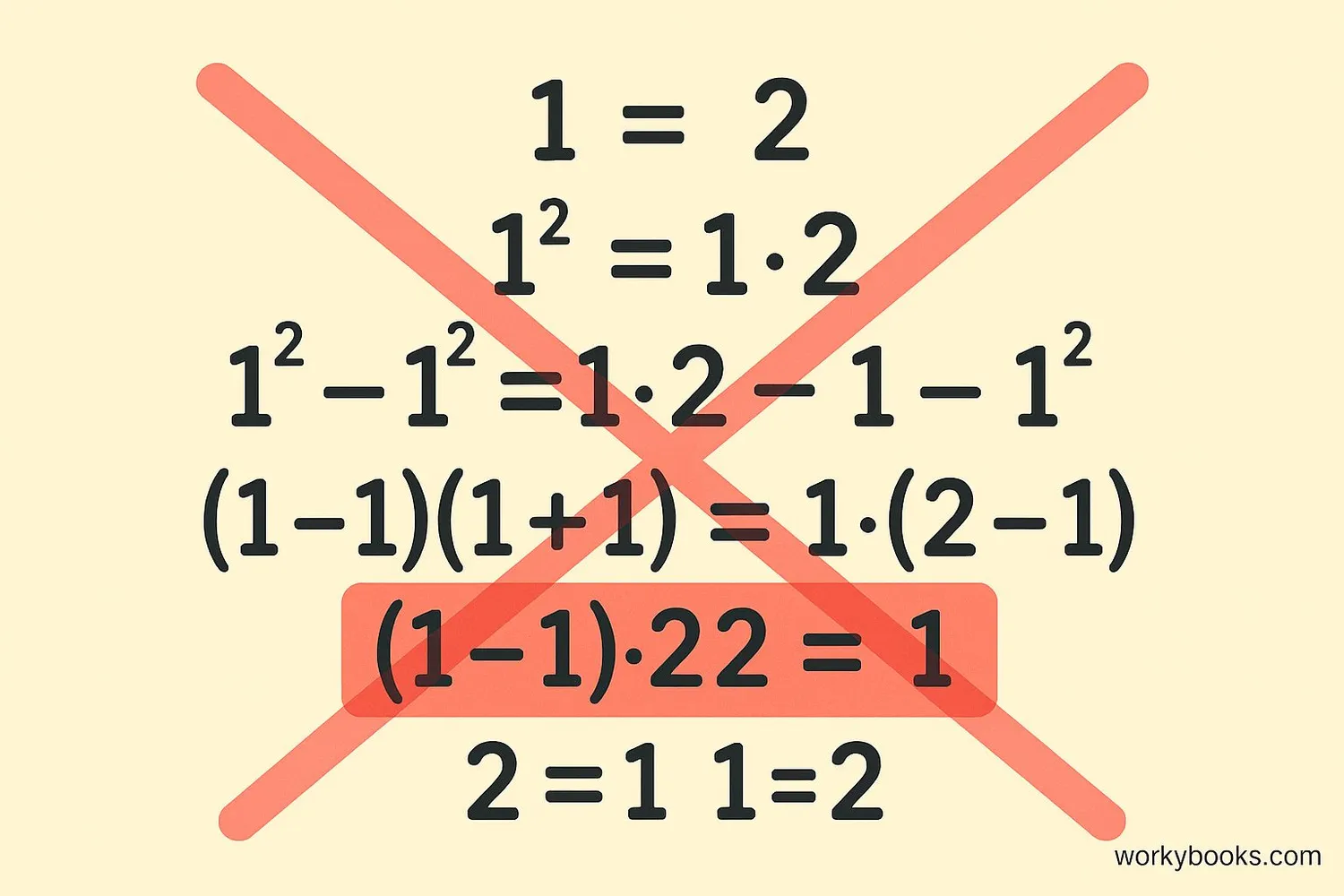
Sometimes people create "false proofs" that seem to show impossible results (like 1 = 2) by secretly dividing by zero. These are called mathematical fallacies.
Here's a common example:
Let a = b
Multiply both sides by a: a² = ab
Subtract b² from both sides: a² - b² = ab - b²
Factor both sides: (a - b)(a + b) = b(a - b)
Divide both sides by (a - b): a + b = b
Since a = b: b + b = b → 2b = b → 2 = 1
The error happens when we divide by (a - b). Since a = b, (a - b) = 0. So we're secretly dividing by zero, which is not allowed! This is why we get the wrong conclusion that 2 = 1.
These fallacies teach us to always check that we're not dividing by zero in our mathematical work.
Watch Out
Always check that the denominator (bottom number) is not zero before dividing. Division by zero can lead to false conclusions.
Zero Divided by Zero

What about 0 ÷ 0? This is a special case called an indeterminate form.
Let's use the multiplication relationship again:
If 0 ÷ 0 = x, then 0 × x should equal 0.
This seems to work for any number x! For example:
0 × 1 = 0, so maybe 0 ÷ 0 = 1
0 × 2 = 0, so maybe 0 ÷ 0 = 2
0 × 100 = 0, so maybe 0 ÷ 0 = 100
Since every number would work, 0 ÷ 0 doesn't have a single definite answer. Mathematicians call this "indeterminate" because it could be any number, and we can't determine which one.
In higher mathematics, 0 ÷ 0 is handled using limits in calculus, but in basic arithmetic, we simply say it's undefined or indeterminate.
Special Case
0 ÷ 0 is indeterminate because it could equal any number, and there's no way to determine which one is correct.
Zero Divided by a Number

While division by zero is undefined, dividing zero by a non-zero number is perfectly fine and equals zero.
For example: 0 ÷ 5 = 0
Why? Because if you have zero cookies and want to share them with 5 friends, each friend gets zero cookies. The multiplication check works too: 0 × 5 = 0.
This rule works for any non-zero number:
Division Rule
Zero divided by any non-zero number equals zero
Rule
Zero divided by any non-zero number equals zero. But division by zero is always undefined.
Division by Zero Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about division by zero:
Math Trivia
Discover interesting facts about division by zero and mathematics:
Historical Perspective
The concept of division by zero has puzzled mathematicians for centuries. The Indian mathematician Brahmagupta was one of the first to discuss division by zero in the 7th century, concluding that zero divided by zero is zero.
Computer Systems
In computer programming, division by zero typically causes a program to crash or throw an exception. Programmers must be careful to check that denominators are not zero before performing division operations.
Real-World Analogy
Imagine trying to distribute zero pizzas to zero people. How many pizzas does each person get? The question doesn't make sense because there are no people to receive pizzas. This illustrates why 0 ÷ 0 is indeterminate.
Mathematical Consistency
If division by zero were allowed, it would break many fundamental mathematical rules and properties. Keeping division by zero undefined preserves the consistency and reliability of mathematics.





