Division Property of Equality - Definition, Examples, Quiz, FAQ, Trivia
Learn how dividing both sides of an equation by the same number keeps it balanced
What is the Division Property of Equality?
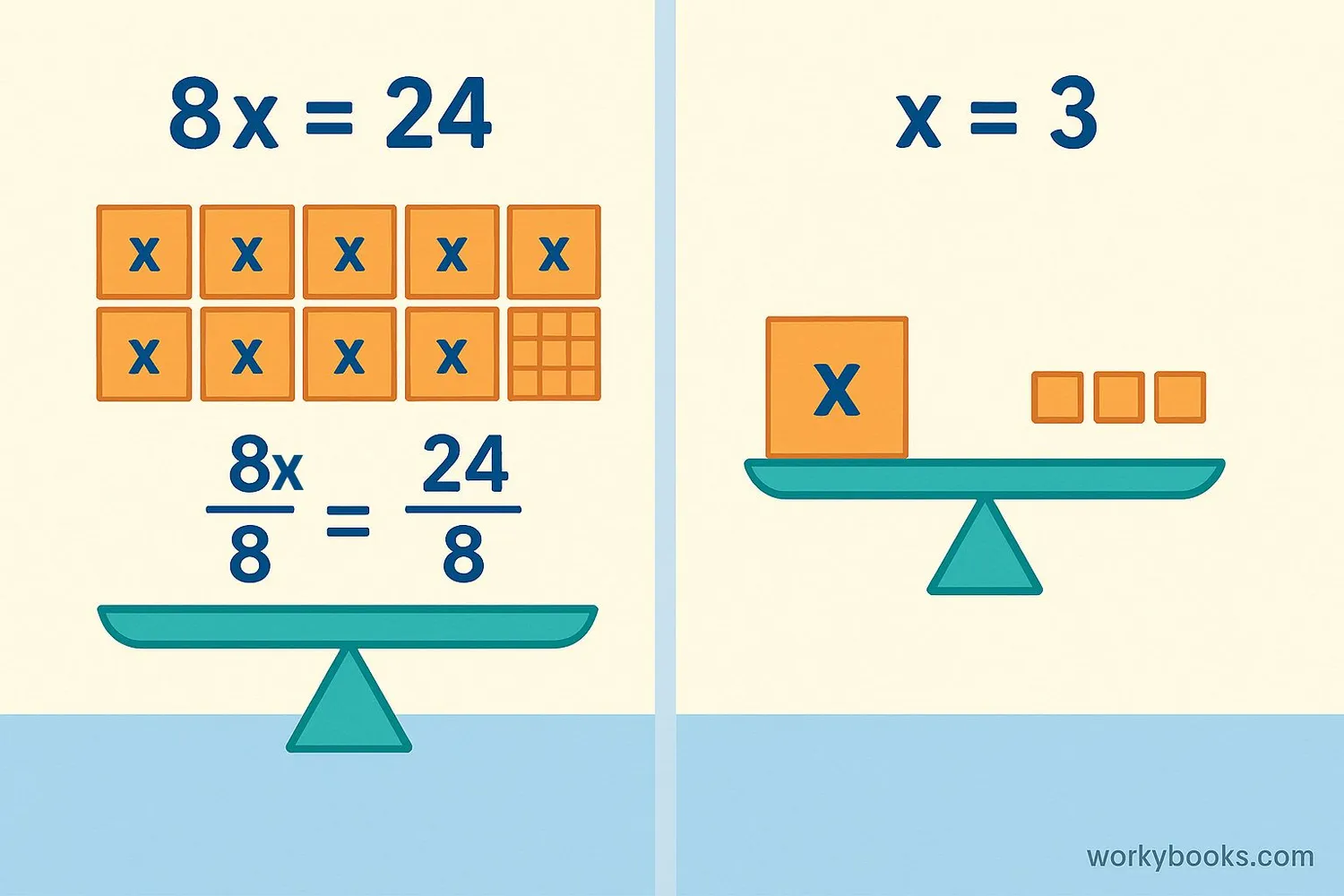
The Division Property of Equality is a mathematical rule that says if you divide both sides of an equation by the same non-zero number, the two sides remain equal.
Think of it like a balanced scale. If you have a scale that's perfectly balanced, and you divide the weight on both sides by the same amount, the scale will stay balanced.
In mathematical terms, if a = b, and c is not zero, then a ÷ c = b ÷ c.
This property helps us solve equations where a variable is being multiplied by a number. We can "undo" the multiplication by dividing both sides.
Division Property Formula
You can divide both sides of an equation by the same non-zero number.
Key Concept
You can never divide by zero! Division by zero is undefined in mathematics and would make the equation invalid.
Examples of Division Property of Equality

Let's look at some examples to understand how the Division Property of Equality works:
Solve: 4x = 12
We divide both sides by 4:
4x ÷ 4 = 12 ÷ 4
x = 3
Solve: 7y = 42
We divide both sides by 7:
7y ÷ 7 = 42 ÷ 7
y = 6
Solve: 15 = 5z
We divide both sides by 5:
15 ÷ 5 = 5z ÷ 5
3 = z
Remember
Always check your solution by substituting it back into the original equation to make sure it works!
Inverse of Division Property

The inverse of the Division Property of Equality is the Multiplication Property of Equality. Just as dividing both sides by the same number keeps the equation balanced, multiplying both sides by the same number also keeps it balanced.
These two properties work together to help us solve equations. If a variable is being multiplied, we use division. If a variable is being divided, we use multiplication.
For example, if we have x ÷ 3 = 4, we would use the Multiplication Property to solve it by multiplying both sides by 3.
Understanding that division and multiplication are inverse operations helps us see how these properties are related.
Inverse Relationship
They "undo" each other, just like addition and subtraction.
Division Property in Algebra

In algebra, the Division Property of Equality is essential for solving equations. It helps us isolate variables and find their values.
When you see an equation like 6x = 24, you know you can divide both sides by 6 to find that x = 4.
This property also works with fractions. For example, if you have (3/4)x = 9, you can divide both sides by 3/4, which is the same as multiplying by 4/3.
The Division Property is one of the fundamental tools that makes algebra work. Without it, we wouldn't be able to solve many types of equations.
Solve: ⅔x = 10
We can divide both sides by ⅔, which is the same as multiplying by 3/2:
x = 10 × (3/2)
x = 30/2
x = 15
Algebra Tip
Dividing by a fraction is the same as multiplying by its reciprocal. This is helpful when working with fractional coefficients.
Practice Quiz
Test your understanding of the Division Property of Equality with this 5-question quiz.
Frequently Asked Questions
Here are answers to common questions about the Division Property of Equality:
Math Trivia
Discover interesting facts about mathematics and the Division Property:
Ancient Equations
The concept of balancing equations dates back to ancient Egyptian and Babylonian mathematicians who used similar principles to solve problems, though they didn't use the algebraic notation we use today.
Real-World Applications
The Division Property of Equality is used in many real-world situations like calculating ingredients in recipes, determining speeds and distances, and converting between measurement systems.
Property Relationships
The Division Property of Equality is one of several properties of equality that also include Addition, Subtraction, Multiplication, Reflexive, Symmetric, and Transitive Properties.
The Problem with Zero
The concept of zero and the problems with dividing by zero troubled mathematicians for centuries. Indian mathematician Brahmagupta first defined zero as a number in the 7th century.





