Empty Set - Definition, Examples, Quiz, FAQ, Trivia
Learn about the special set that has no elements with easy explanations and practice activities
What is an Empty Set?

In mathematics, a set is a collection of different things, which we call elements. An empty set is a special set that has no elements at all.
Think of it like an empty lunchbox. When you look inside, there's nothing there - no sandwich, no fruit, no cookies. The empty set is just like that empty lunchbox - it's a collection with nothing in it.
The empty set is also called the null set or the void set. It's important in mathematics because it's the starting point for building other sets, just like zero is the starting point for numbers.
Key Concept
The empty set is the only set that has no elements. It's unique and very important in mathematics!
Notation and Symbols
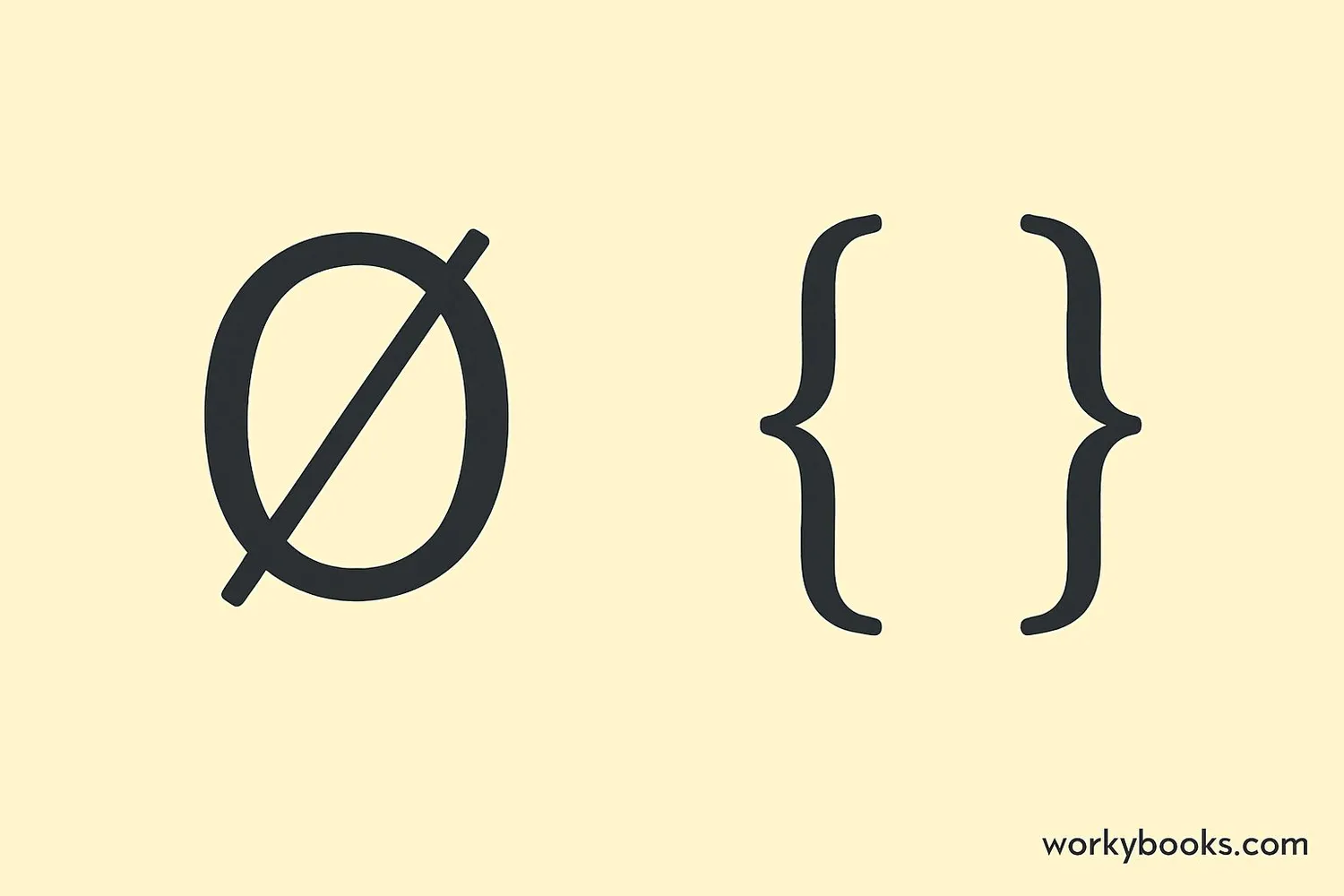
Mathematicians use special symbols to represent the empty set. There are two main ways to write it:
Empty Set Notation
These both mean "the empty set"
Both of these notations mean exactly the same thing: a set with no elements. You might see either one used in math books or worksheets.
Remember
{ } does NOT mean zero! It means a set with nothing in it. The empty set is different from the number zero.
Real Examples of Empty Sets
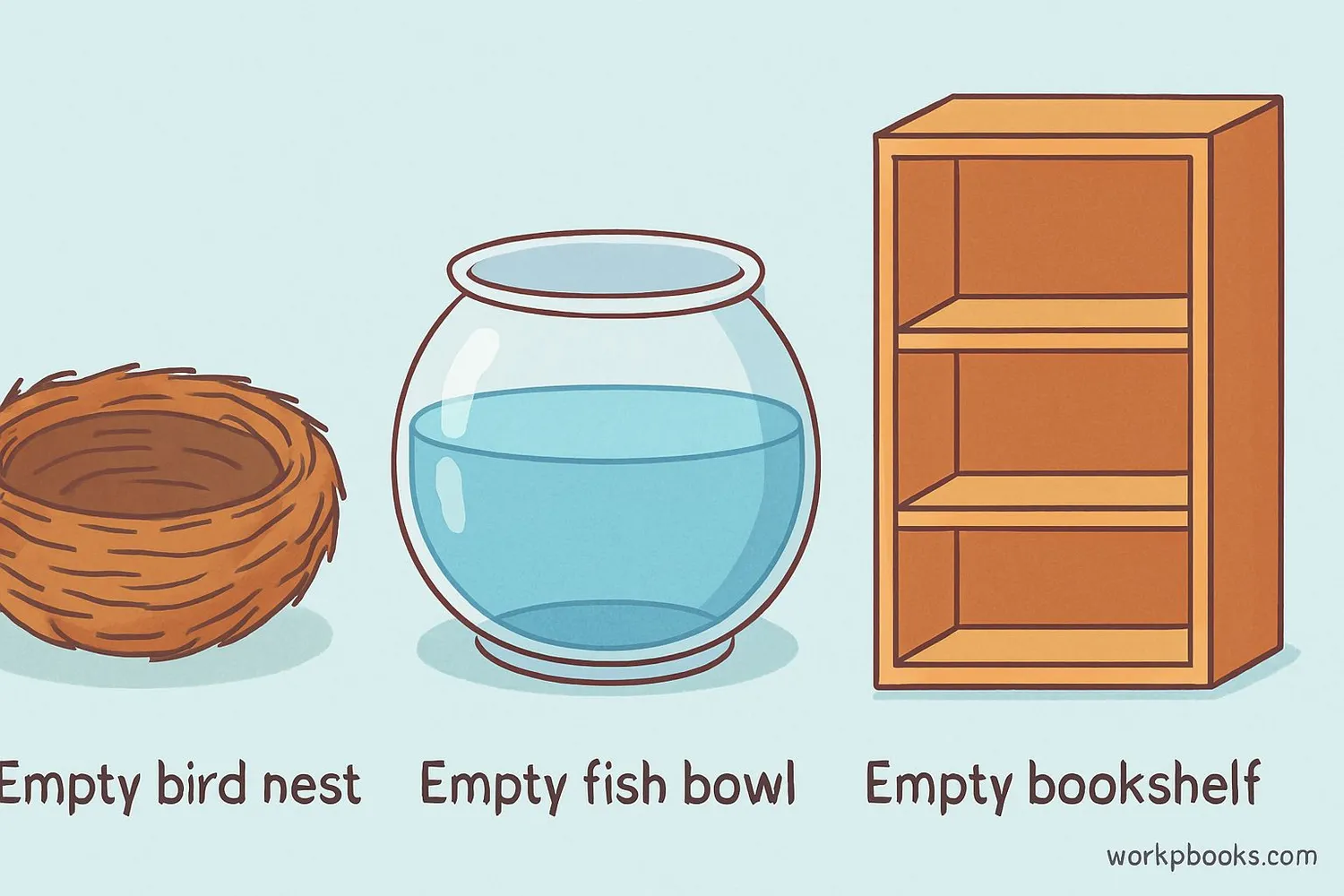
Empty sets aren't just math concepts - we find them in real life too! Here are some examples:
Example 1: The set of elephants in your classroom. Unless you have a very unusual classroom, this set is empty!
Example 2: The set of fish that can fly. Fish live in water and can't fly, so this set is empty.
Example 3: The set of three-sided squares. Squares have four sides, so a three-sided square can't exist. Empty set!
Example 4: The set of students in your class who are 100 years old. Since elementary students are much younger, this set is empty.
Can you think of other empty sets? How about the set of cars that can talk? Or the set of pencils that are made of chocolate?
Real Life Tip
Whenever you can describe a group of things that doesn't actually contain anything, you've found an empty set!
Special Properties
The empty set has some special properties that make it unique in mathematics:
1. Subset of Everything: The empty set is a subset of every other set. That means if you have any set at all - like the set of fruits or the set of numbers - the empty set is always contained within it.
2. Only One Empty Set: There is only one empty set. It doesn't matter if we're talking about empty sets of animals, numbers, or colors - there's only one unique empty set.
3. Cardinality Zero: The number of elements in a set is called its "cardinality." The empty set has cardinality zero because it has no elements.
4. Foundation for Other Sets: Just like zero is the foundation for numbers, the empty set is the foundation for building all other sets in mathematics.
Math Fact
The empty set is like the number zero of set theory - it might represent "nothing," but it's very important!
Empty Set Practice Quiz
Test your understanding of the empty set with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the empty set:
Math Trivia
Discover interesting facts about sets and mathematics:
Historical Origins
The concept of the empty set was first formally introduced by mathematician Georg Cantor in the late 19th century when he developed set theory, which is now fundamental to modern mathematics.
Computer Science
In computer programming, the empty set concept is used in databases and programming languages. For example, an empty array or empty list represents a collection with no elements.
Set Theory Foundation
All of mathematics can be built up from just two concepts: the empty set and the idea of putting things together to form sets. This shows how important the empty set is to math!
Unique Properties
The empty set is the only set that is a subset of every other set. It's also the only set with cardinality zero. These special properties make it unique in mathematics.





