Equiangular Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about special triangles with equal angles and their properties
What is an Equiangular Triangle?
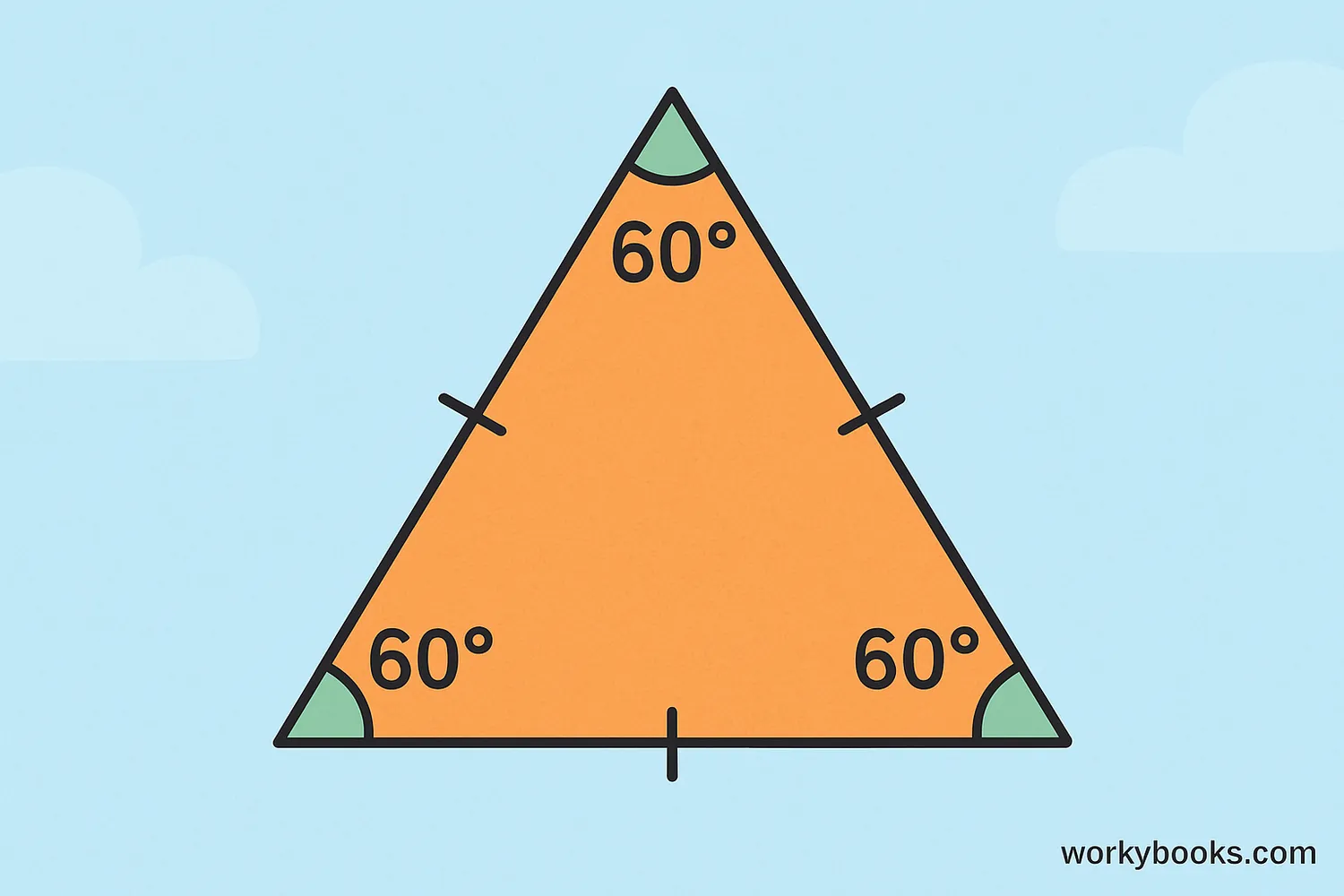
An equiangular triangle is a special type of triangle where all three interior angles are equal. Since the sum of all angles in any triangle is always 180 degrees, each angle in an equiangular triangle measures exactly 60 degrees.
The word "equiangular" comes from two Latin words: "aequus" meaning equal, and "angulus" meaning angle. So equiangular literally means "equal angles."
An important fact about equiangular triangles is that they are also equilateral triangles, meaning all three sides are the same length. This makes them regular polygons, which are shapes with equal angles and equal sides.
Key Concept
In an equiangular triangle, all three angles are equal to 60°, and all three sides are equal in length.
Properties of Equiangular Triangles
Equiangular triangles have several special properties that make them unique:
| Property | Description |
|---|---|
| Angles | All three angles are equal to 60° |
| Sides | All three sides are equal in length |
| Symmetry | Has three lines of symmetry |
| Rotation | Has rotational symmetry of order 3 |
| Altitude | The altitude, median, and angle bisector from each vertex are the same |
| Area | Area = (√3/4) × side² |
| Perimeter | Perimeter = 3 × side length |
Remember
Every equiangular triangle is also equilateral, and every equilateral triangle is also equiangular. These terms are often used interchangeably.
Types of Triangles
Triangles can be classified based on their sides or angles. Understanding these classifications helps us recognize the special properties of equiangular triangles:
Classification by Sides
| Type | Description | Properties |
|---|---|---|
| Equilateral | All three sides equal | All angles equal (60° each) |
| Isosceles | Two sides equal | Two angles equal |
| Scalene | No sides equal | No angles equal |
Classification by Angles
| Type | Description | Properties |
|---|---|---|
| Acute | All angles less than 90° | Equiangular triangles are acute |
| Right | One angle exactly 90° | Other two angles add to 90° |
| Obtuse | One angle greater than 90° | Other two angles add to less than 90° |
Classification Tip
Equiangular triangles are always acute triangles because all their angles are less than 90°. They are also always equilateral triangles.
Real-World Examples
Equiangular triangles appear in many real-world contexts. Here are some examples:
Road Signs: Yield signs are often equilateral triangles, which means they are also equiangular.
Architecture: Many structures use triangular supports because triangles are strong and stable. The equiangular triangle is especially stable.
Nature: Some crystals and molecular structures form equiangular triangles. Snowflakes often contain equiangular triangular patterns.
Art and Design: Equilateral triangles are used in patterns, logos, and designs because of their balanced and pleasing appearance.
Mathematics: Equiangular triangles are used in trigonometry and geometry problems because of their predictable properties.
Real-World Connection
Look around you—you might be surprised how many equiangular triangles you can find in everyday objects and structures!
Triangle Knowledge Quiz
Test your understanding of equiangular triangles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about equiangular triangles:
Geometry Trivia
Discover interesting facts about triangles and geometry:
Ancient Geometry
The ancient Egyptians used triangles and their properties to re-establish land boundaries after the annual flooding of the Nile River. This practice, called "surveying," may be one of the earliest applications of geometry.
Triangle Sum
No matter what type of triangle you have (equiangular, right, scalene, etc.), the sum of its three interior angles will always be 180 degrees. This is known as the Triangle Sum Theorem.
Triangles in Nature
Many natural structures use triangular forms because they provide strength and stability. Examples include the hexagonal patterns in honeycombs (made of triangles), the structure of crystals, and the arrangement of leaves on some plants.
Architectural Strength
Triangles are the strongest geometric shape because they distribute weight evenly. This is why you see triangular supports in bridges, towers, and roofs. The equiangular triangle is especially stable due to its symmetry.





