Equilateral Triangles - Definition, Examples, Quiz, FAQ, Trivia
Learn about these special triangles with equal sides and equal angles
What is an Equilateral Triangle?
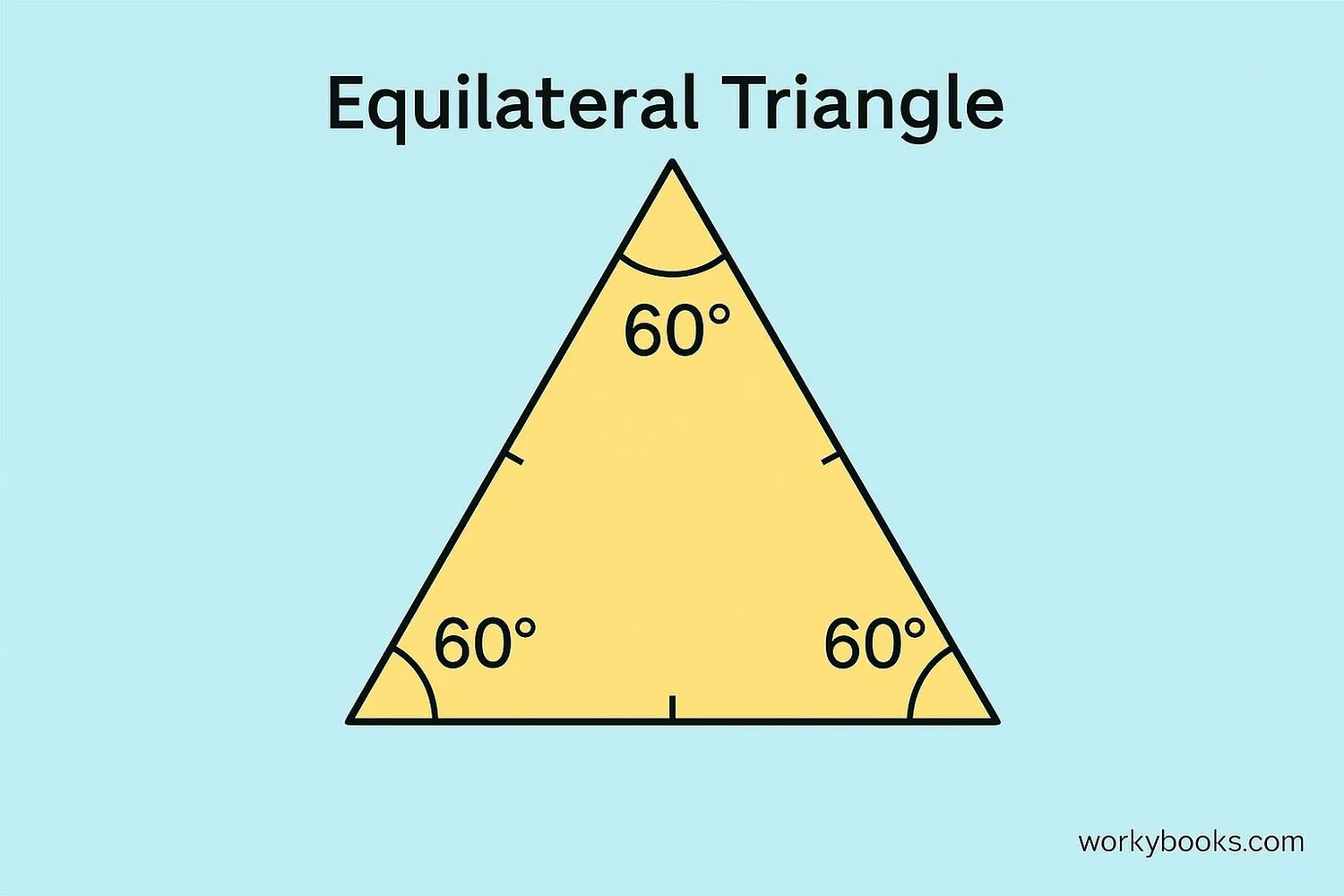
An equilateral triangle is a special type of triangle where all three sides are exactly the same length, and all three angles are exactly the same size.
The word "equilateral" comes from Latin: "equi" means equal, and "lateral" means sides. So it literally means "equal sides".
Since all three angles in a triangle always add up to 180 degrees, and all angles are equal in an equilateral triangle, each angle must be 60 degrees (180 ÷ 3 = 60).
Key Facts
1. All sides are equal
2. All angles are 60 degrees
3. It's a regular polygon
Types of Triangles
Equilateral
All sides equal
All angles 60°
Isosceles
Two sides equal
Two angles equal
Scalene
All sides different
All angles different
Properties of Equilateral Triangles
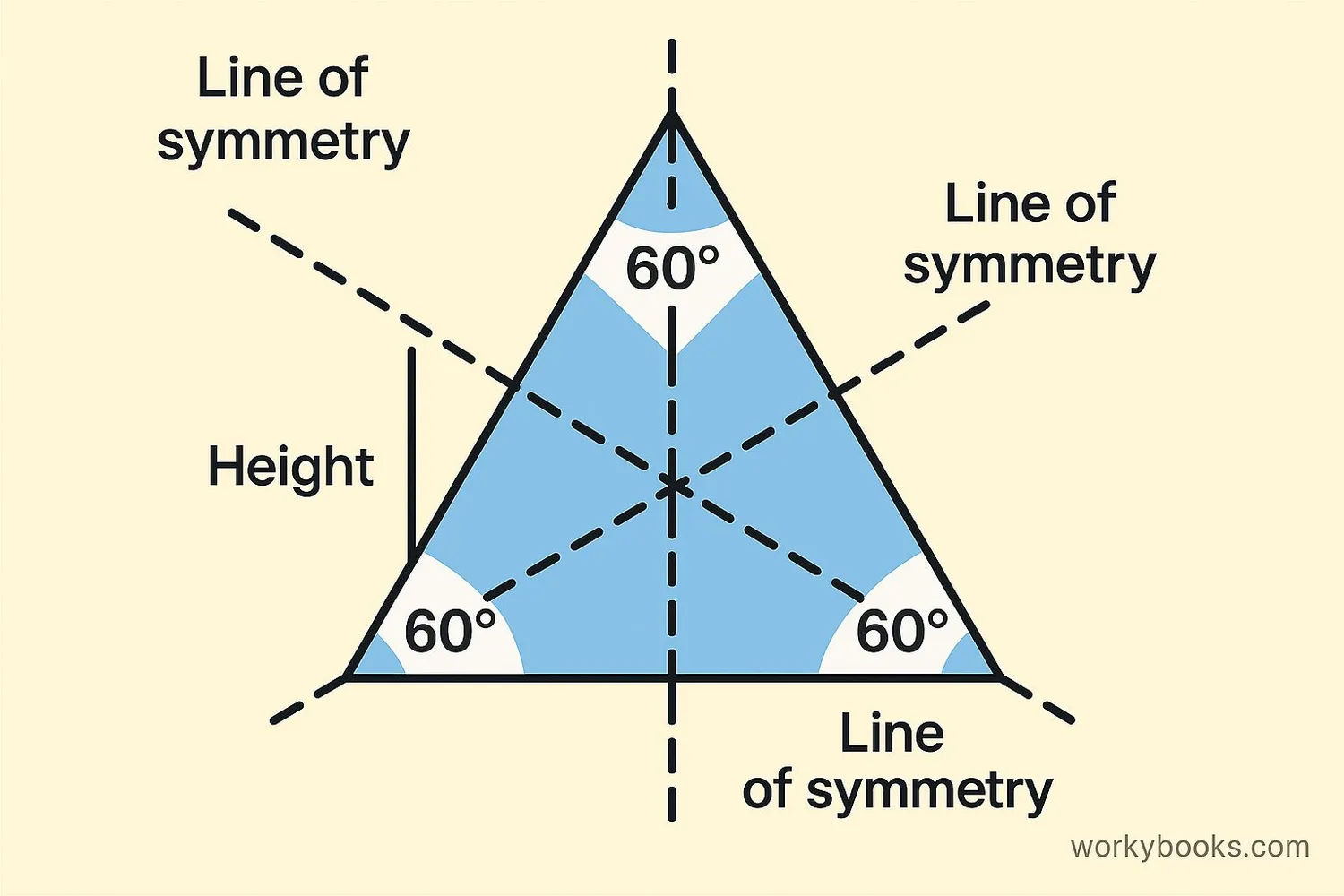
Equilateral triangles have many special properties that make them unique:
Equal Sides
All three sides are exactly the same length. If one side is 5 cm, then all sides are 5 cm.
Equal Angles
All three angles are exactly 60 degrees each. This makes it an equiangular triangle too.
Symmetry
An equilateral triangle has three lines of symmetry. Each line goes from a vertex to the midpoint of the opposite side.
Regular Polygon
It's the only triangle that is a regular polygon because all sides and all angles are equal.
Height
The height (h) can be calculated using the formula: h = (√3/2) × side length
Rotational Symmetry
It has rotational symmetry of order 3. This means it looks the same after rotating it 120°, 240°, or 360°.
Formulas for Equilateral Triangles
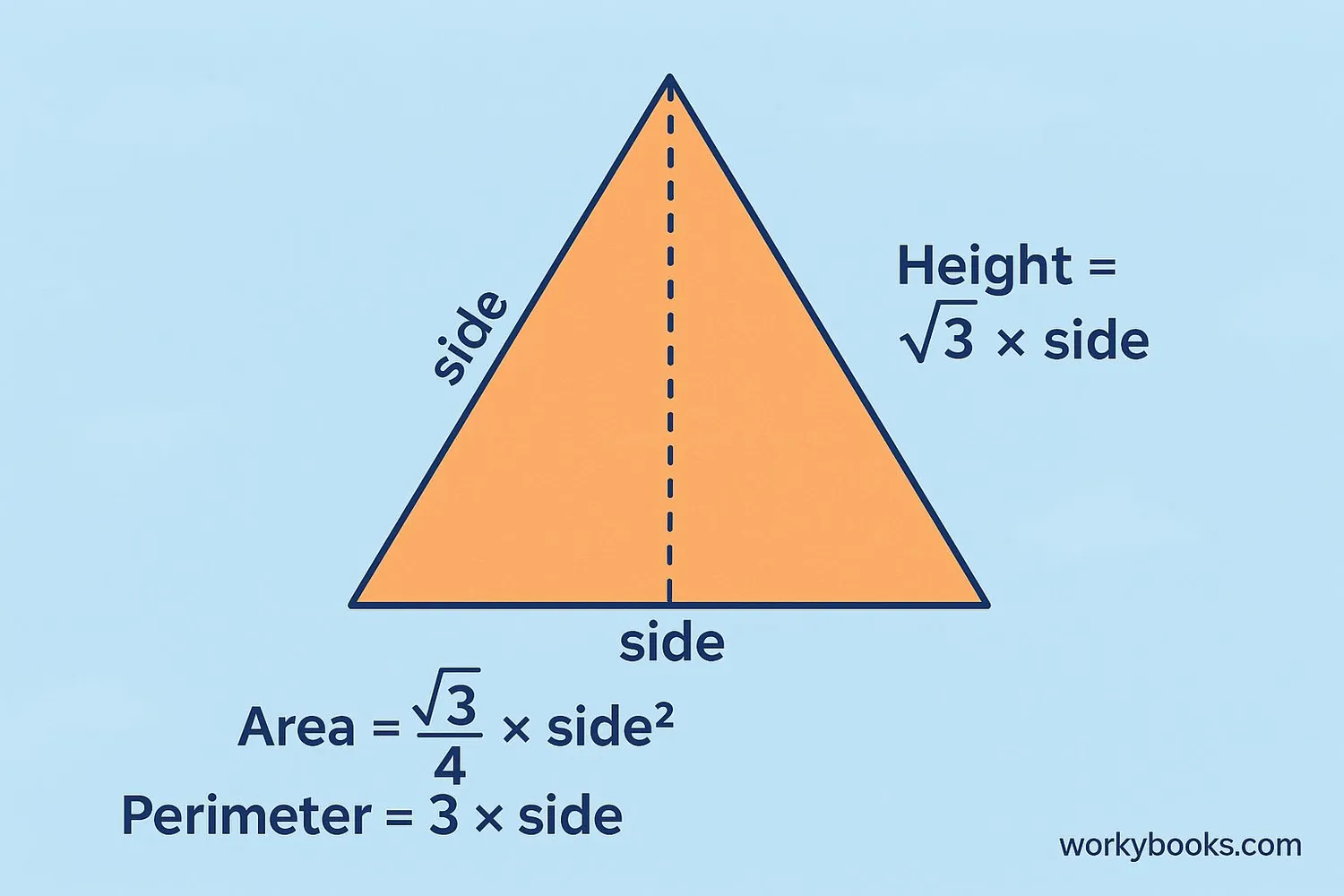
Because all sides are equal in an equilateral triangle, we have special formulas to calculate its area, perimeter, and height:
Perimeter Formula
Where "a" is the length of one side.
Area Formula
Where "a" is the length of one side.
Height Formula
Where "a" is the length of one side.
Example Calculation
For an equilateral triangle with side length 6 cm:
Perimeter = 3 × 6 = 18 cm
Area = (√3 ÷ 4) × 6² ≈ (1.732 ÷ 4) × 36 ≈ 15.588 cm²
Height = (√3 ÷ 2) × 6 ≈ (1.732 ÷ 2) × 6 ≈ 5.196 cm
Special Centers
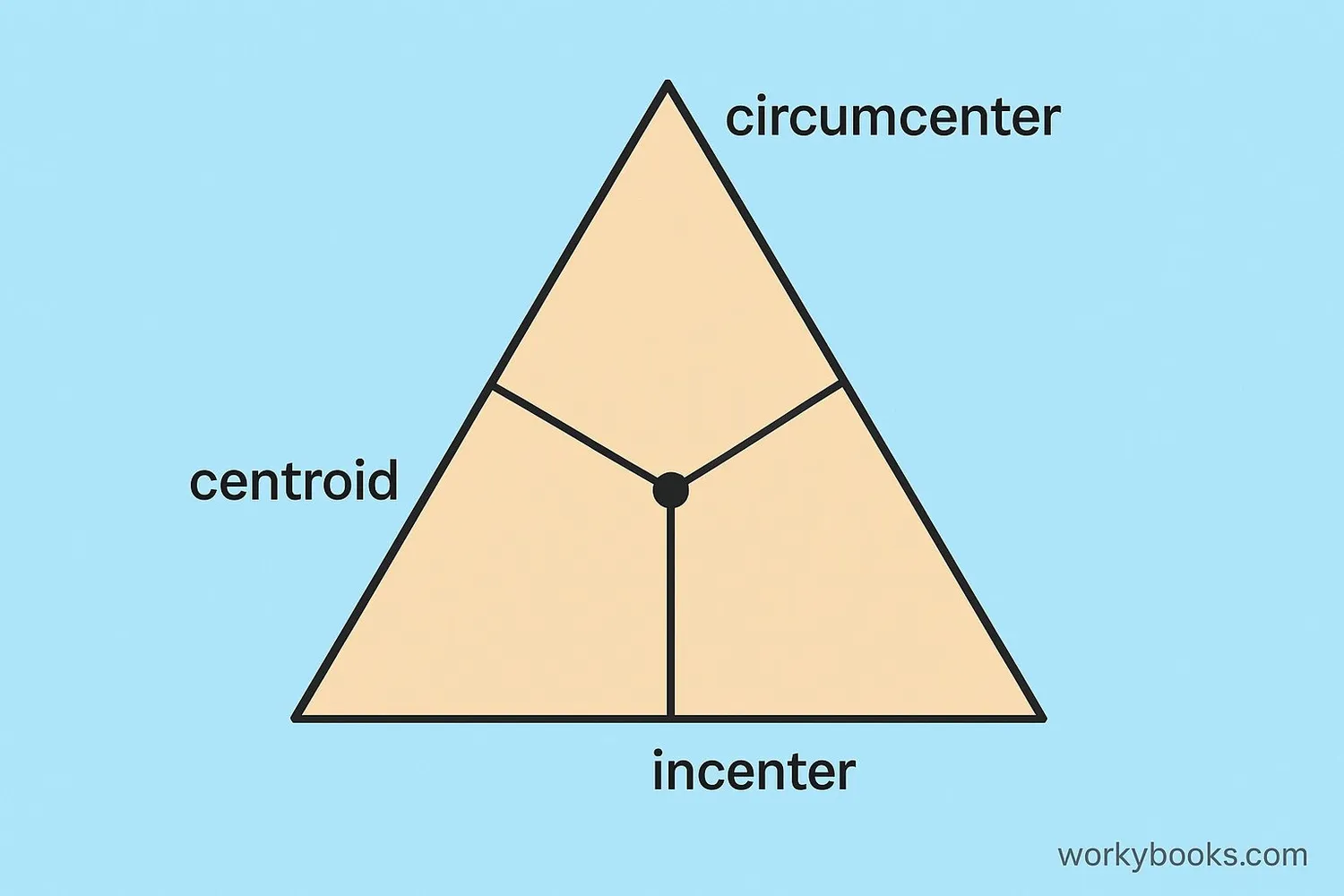
In equilateral triangles, several important points coincide at the exact same location:
Centroid
The point where all three medians meet. The centroid is also the center of gravity of the triangle.
Circumcenter
The center of the circumcircle (circle passing through all three vertices).
Incenter
The center of the incircle (circle tangent to all three sides).
Orthocenter
The point where all three altitudes intersect.
Unique Property
In equilateral triangles, the centroid, circumcenter, incenter, and orthocenter all coincide at the same point!
Real-Life Examples

Equilateral triangles appear in many places in our world. Here are some common examples:
Road Signs
Yield signs are equilateral triangles pointing downward.
Architecture
Truss bridges often use equilateral triangles for strength and stability.
Crystals
Some crystal structures form in equilateral triangular patterns.
Food
Tortilla chips, pizza slices, and some sandwiches are cut in equilateral triangles.
Games
Many board games use equilateral triangles for game pieces or board spaces.
Nature
Some leaves, snowflakes, and rock formations show equilateral triangular patterns.
Equilateral Triangle Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about equilateral triangles:
Geometry Trivia
Discover interesting facts about triangles and geometry:
Ancient Discovery
Equilateral triangles were studied by ancient mathematicians in Egypt and Babylon over 4000 years ago. The ancient Egyptians used them in pyramid construction.
Strongest Shape
Equilateral triangles are considered the strongest geometric shape. This is why they're used in bridges and towers - they distribute weight evenly without bending.
Nature's Triangles
Bees build honeycombs with hexagonal cells, but each hexagon is made of six equilateral triangles! This efficient shape uses the least wax to store the most honey.
Mathematical Constant
The area of an equilateral triangle is exactly √3/4 times the square of its side length. The √3 is an irrational number (approximately 1.732) that appears in many geometric formulas.





