Equivalent - Definition, Examples, Quiz, FAQ, Trivia
Learn what equivalent means with easy explanations, visual examples, and practice activities
What Does Equivalent Mean?

In mathematics, equivalent means having the same value or amount. When we say two things are equivalent, they may look different but have the same value.
Think of it like different ways to express the same thing. For example, 2+2 is equivalent to 4 because they both represent the same amount. The equals sign (=) shows that two expressions are equivalent.
Understanding equivalence helps us solve problems in different ways and recognize that there can be multiple paths to the same answer. This concept is used throughout mathematics, from basic arithmetic to algebra and beyond.
Key Concept
Equivalent means "equal in value, function, or meaning." Two mathematical expressions are equivalent if they simplify to the same value or represent the same relationship.
Examples of Equivalent
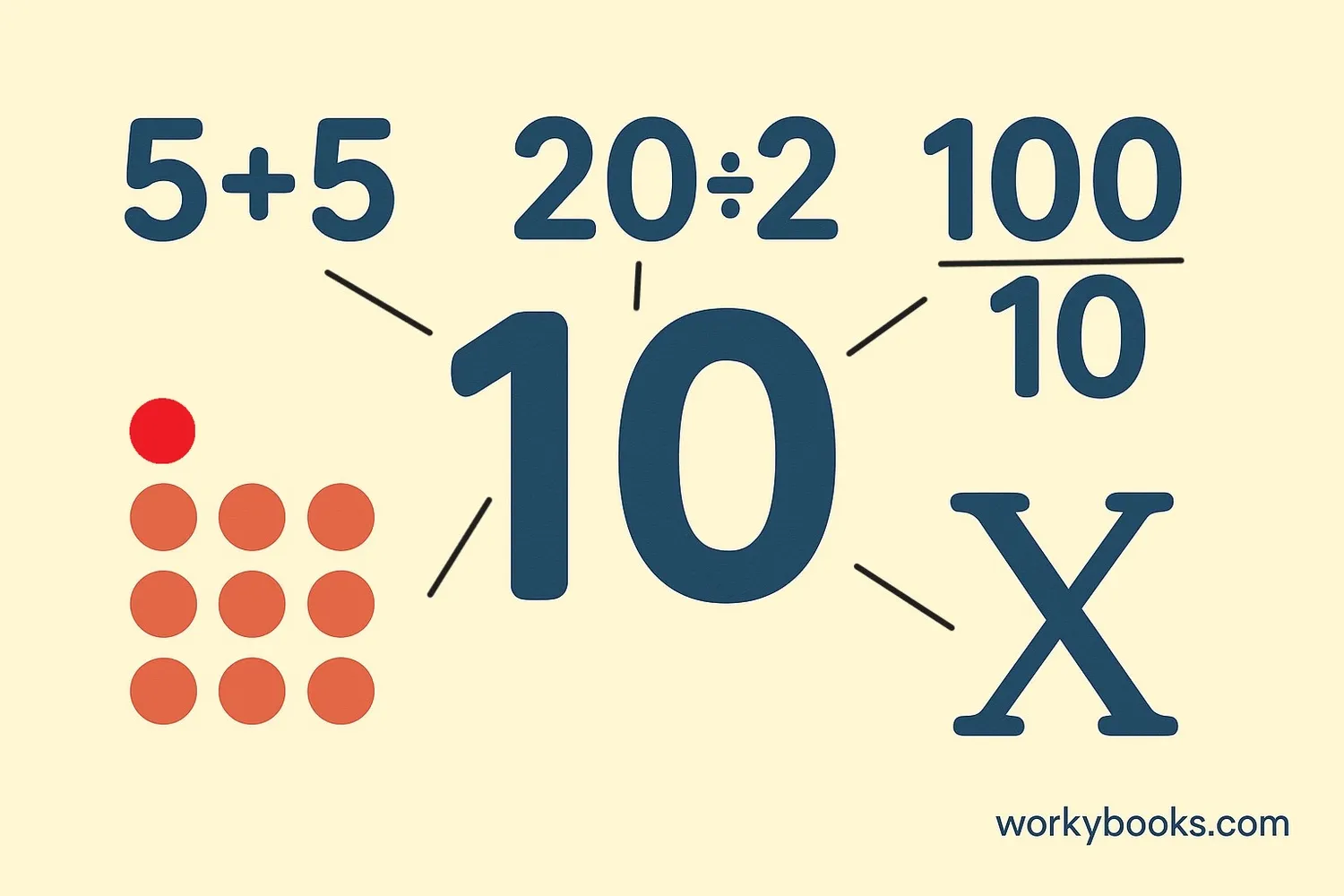
Let's look at some examples of equivalent expressions:
Numbers
5 + 5 = 10
20 - 10 = 10
2 × 5 = 10
100 ÷ 10 = 10
All these expressions are equivalent because they all equal 10.
Measurements
12 inches = 1 foot
3 feet = 1 yard
100 centimeters = 1 meter
16 ounces = 1 pound
These measurements are equivalent even though they use different units.
Money
4 quarters = 1 dollar
10 dimes = 1 dollar
100 pennies = 1 dollar
20 nickels = 1 dollar
Different coins can have equivalent value to paper money.
Remember
Equivalent doesn't always mean identical. Things can look different but still be equivalent in value.
Equivalent Fractions
Fractions can be equivalent too! Equivalent fractions are different fractions that name the same amount.
For example, 1/2 is equivalent to 2/4, 3/6, and 4/8. Even though these fractions look different, they all represent the same value.
We can create equivalent fractions by multiplying or dividing both the numerator (top number) and denominator (bottom number) by the same number. This is like splitting something into more pieces but taking more of those pieces.
Creating Equivalent Fractions
Multiply both numerator and denominator by the same number to create an equivalent fraction.
Example 1
1/2 = 2/4 = 3/6 = 4/8
All these fractions represent half of something.
Example 2
2/3 = 4/6 = 6/9 = 8/12
These fractions all represent two-thirds of a whole.
Example 3
3/4 = 6/8 = 9/12 = 12/16
These fractions all represent three-quarters of a whole.
Equivalent Expressions
In algebra, equivalent expressions are expressions that simplify to the same value for all values of the variables. This means no matter what number you substitute for the variable, both expressions will give the same result.
For example, 2(x + 3) is equivalent to 2x + 6. If we let x = 1, then 2(1 + 3) = 8 and 2(1) + 6 = 8. If we let x = 5, then 2(5 + 3) = 16 and 2(5) + 6 = 16.
Recognizing equivalent expressions helps us simplify problems and solve equations more efficiently.
Distributive Property
3(x + 4) = 3x + 12
5(2y - 3) = 10y - 15
2(a + b) = 2a + 2b
Multiplying a number by a sum is equivalent to multiplying by each term separately.
Combining Like Terms
2x + 3x = 5x
4y - y = 3y
3a + 2b + 5a - b = 8a + b
Simplifying expressions by combining terms with the same variables.
Commutative Property
2 + 5 = 5 + 2
3 × 4 = 4 × 3
a + b = b + a
x × y = y × x
The order of numbers in addition or multiplication doesn't change the result.
Algebra Tip
To check if two expressions are equivalent, try substituting the same number for the variable in both expressions. If they give the same result, they might be equivalent (though you should test with several numbers to be sure).
Practice Quiz
Test your understanding of equivalent concepts with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about equivalent concepts:
Math Trivia
Discover interesting facts about equivalence in mathematics:
History of the Equals Sign
The equals sign (=) was invented by Welsh mathematician Robert Recorde in 1557. He used two parallel lines because "no two things can be more equal." Before this, mathematicians wrote out the word "equals."
The Three Lines Symbol
Mathematicians sometimes use a special symbol (≡) to show that two things are identical or always equivalent. This is different from the equals sign (=) which shows that two expressions have the same value.
Equivalent in Computers
Computers use the concept of equivalence in programming. The double equals sign (==) is often used to test if two values are equivalent, while a single equals sign (=) is used for assignment (giving a variable a value).
Different Number Systems
Different cultures developed equivalent number systems independently. Roman numerals (I, V, X), Arabic numerals (1, 2, 3), and Chinese numerals (一, 二, 三) all represent equivalent values despite looking completely different.





