Equivalent Fractions - Definition, Examples, Quiz, FAQ, Trivia
Learn how different fractions can represent the same value with visual examples and activities
What Are Equivalent Fractions?
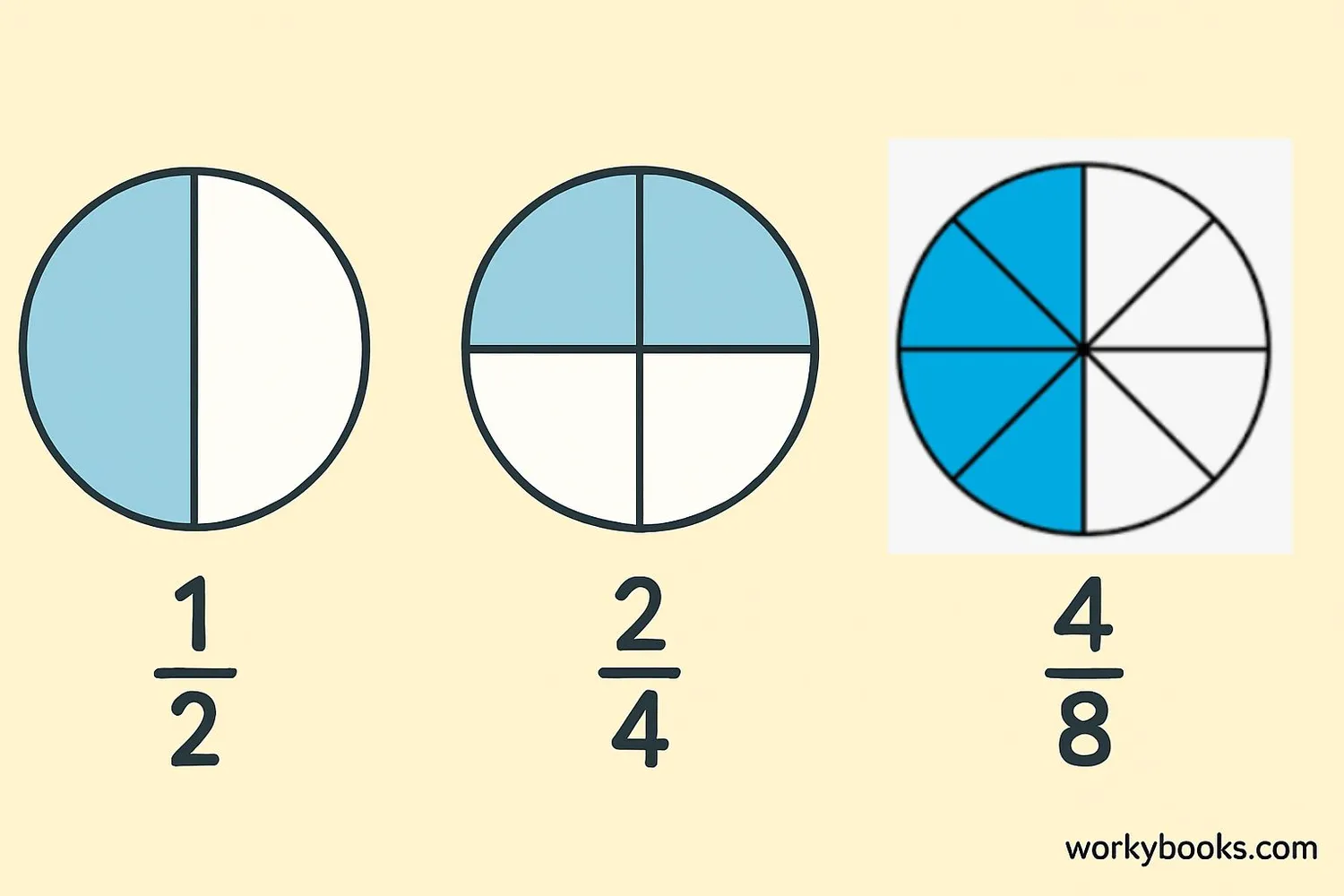
Equivalent fractions are different fractions that represent the same value or the same part of a whole. Even though they look different, they have the same value when simplified.
For example, 1/2, 2/4, and 3/6 are all equivalent fractions because they all represent the same amount - half of a whole. Think of it like different names for the same number!
Why are equivalent fractions important? They help us compare different fractions, add and subtract fractions with different denominators, and simplify complex fractions. Understanding equivalent fractions is a key skill in math that you'll use throughout your learning.
Key Concept
Equivalent fractions represent the same portion of a whole, even though they use different numbers in the numerator and denominator.
How to Find Equivalent Fractions
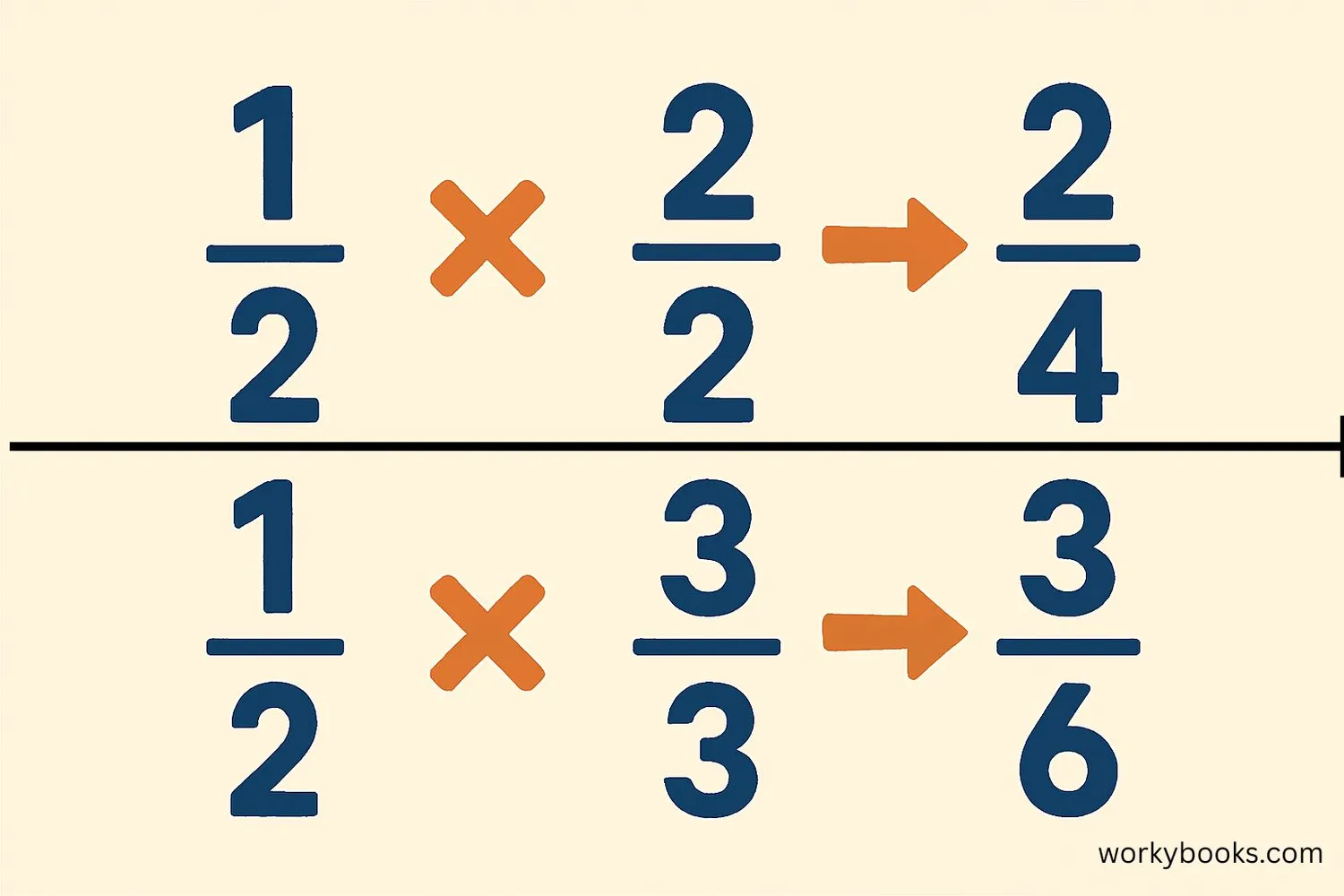
There are two simple ways to find equivalent fractions:
1. Multiply the numerator and denominator by the same number:
If you multiply both the top number (numerator) and the bottom number (denominator) by the same value, you get an equivalent fraction.
Equivalent Fraction Rule
Where c is any number (except zero!)
Multiply numerator and denominator by 2: (1×2)/(2×2) = 2/4
Multiply by 3: (1×3)/(2×3) = 3/6
Multiply by 4: (1×4)/(2×4) = 4/8
2. Divide the numerator and denominator by the same number:
If you can divide both the top and bottom by the same number, you get a simpler equivalent fraction (this is called simplifying).
Example: Simplify 4/8
Divide numerator and denominator by 4: (4÷4)/(8÷4) = 1/2
Remember
You can multiply or divide by any number except zero! The fraction must always have whole numbers in both numerator and denominator.
Visualizing Equivalent Fractions
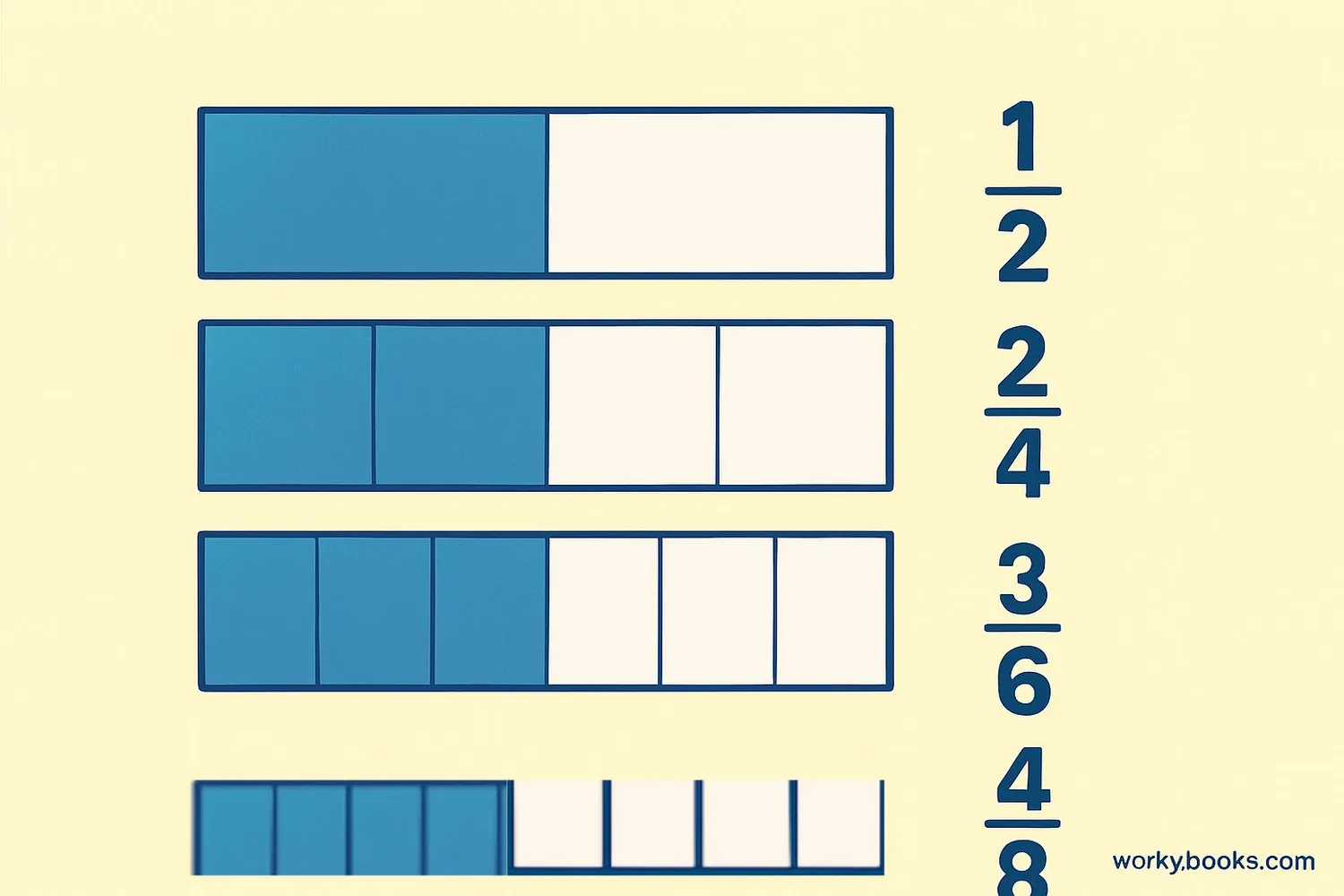
Visual models help us understand that different fractions can represent the same amount. Look at the fraction bars above - even though they're divided into different numbers of parts, the shaded portion is exactly the same size for 1/2, 2/4, and 3/6.
Try this with a piece of paper:
1. Fold a paper in half and shade one half
2. Now fold the same paper into fourths and shade two fourths
3. Notice that the shaded areas are the same!
Visual Tip
The more pieces you divide something into, the smaller each piece becomes, but the total amount remains the same!
Equivalent Fractions Chart
This chart shows some common fractions and their equivalents. You can use this as a reference when working with fractions:
Equivalent Fractions Reference
| Fraction | Equivalent Fractions |
|---|---|
| 1/2 | 2/4, 3/6, 4/8, 5/10, 6/12 |
| 1/3 | 2/6, 3/9, 4/12 |
| 2/3 | 4/6, 6/9, 8/12 |
| 1/4 | 2/8, 3/12 |
| 3/4 | 6/8, 9/12 |
| 1/5 | 2/10, 3/15 |
| 2/5 | 4/10, 6/15 |
1/2
2/4, 3/6, 4/8, 5/10
1/3
2/6, 3/9, 4/12
1/4
2/8, 3/12, 4/16
3/4
6/8, 9/12, 12/16
Chart Tip
Notice how the equivalent fractions for 1/2 are all even numbers? That's because when you multiply both parts by 2, you get the next equivalent fraction!
Examples of Equivalent Fractions

Let's practice with some examples:
Example 1: Are 2/3 and 4/6 equivalent?
Solution: Multiply 2/3 by 2/2: (2×2)/(3×2) = 4/6. Yes, they are equivalent!
Example 2: Find three fractions equivalent to 3/4.
Solution:
Multiply by 2: (3×2)/(4×2) = 6/8
Multiply by 3: (3×3)/(4×3) = 9/12
Multiply by 4: (3×4)/(4×4) = 12/16
Example 3: Simplify 8/12 to its simplest form.
Solution: Find the greatest common factor of 8 and 12, which is 4.
Divide numerator and denominator by 4: (8÷4)/(12÷4) = 2/3
Example 4: Are 5/10 and 1/2 equivalent?
Solution: Simplify 5/10 by dividing both by 5: (5÷5)/(10÷5) = 1/2. Yes!
Practice Tip
To check if two fractions are equivalent, cross-multiply. If a×d = b×c, then a/b = c/d.
Equivalent Fractions Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about equivalent fractions:
Fraction Trivia
Discover interesting facts about fractions:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They had special symbols for fractions like 1/2, 1/3, and 2/3, but represented other fractions as sums of unit fractions.
Fractions in Nature
Fractions appear everywhere in nature! Flower petals often come in fractions of Fibonacci numbers (like 3/5 or 5/8), and honeycombs are made of hexagonal cells that can be divided into fractional parts.
Fractions in Music
Musical rhythms are built on fractions! A whole note gets 4 beats, a half note gets 2 beats, a quarter note gets 1 beat, and so on. Musicians use fractions every time they read music!
Pizza Fractions
The world's largest pizza was made in Rome in 2012. It was 1261.65 square meters! If divided equally among 1000 people, each person would get about 1.26 square meters of pizza - that's a fraction too!





