Equivalent Ratios - Definition, Examples, Quiz, FAQ, Trivia
Learn how ratios work and discover how different ratios can represent the same relationship
What are Ratios?
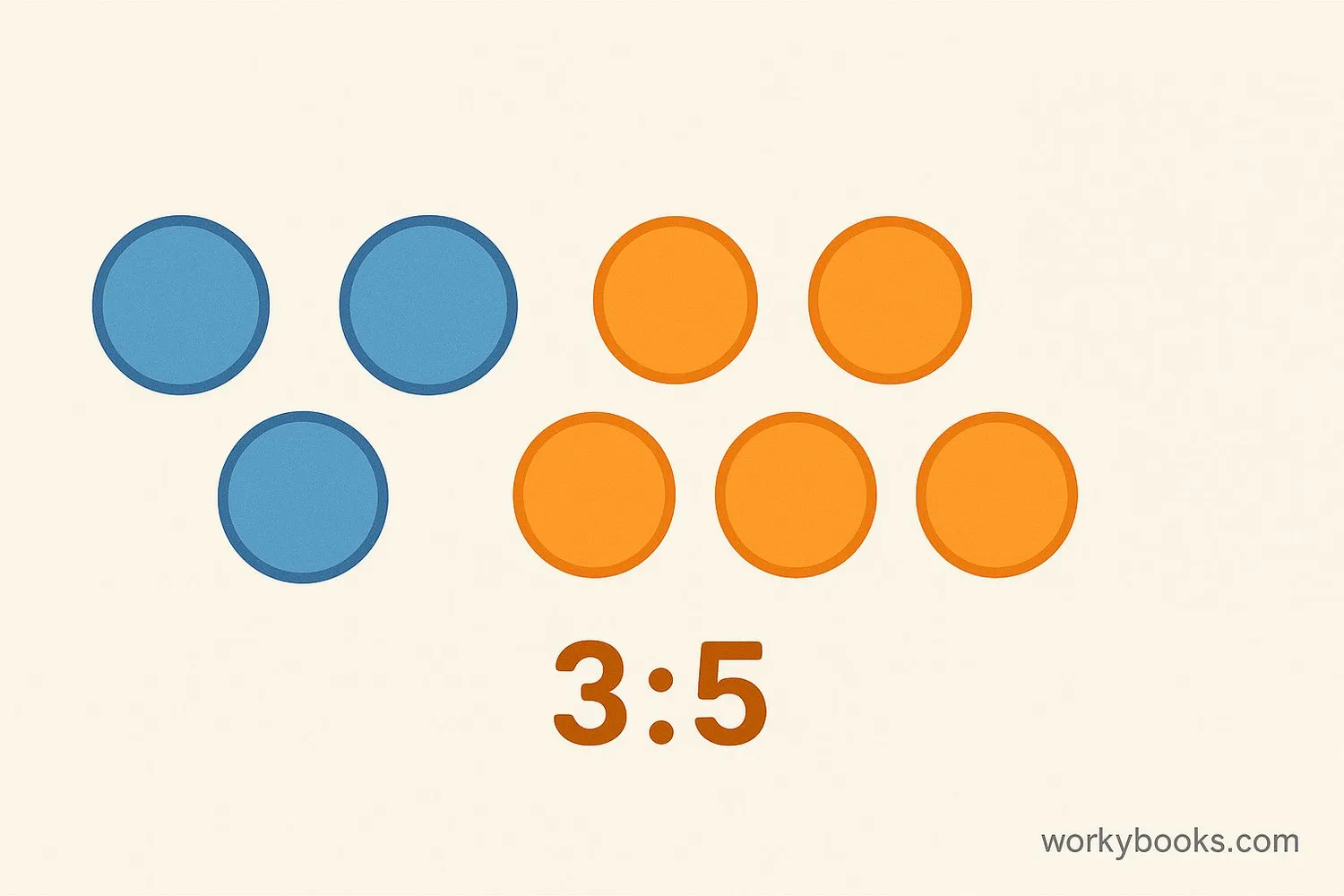
A ratio is a way to compare two or more quantities. It shows how much of one thing there is compared to another. We write ratios with a colon (:) between the numbers.
For example, if you have 3 apples and 5 oranges, the ratio of apples to oranges is 3:5. This means for every 3 apples, there are 5 oranges.
Ratios are everywhere in our daily lives:
- Recipes: 2 cups of flour to 1 cup of sugar (2:1 ratio)
- Sports: 3 wins to 2 losses (3:2 ratio)
- Maps: 1 inch represents 10 miles (1:10 ratio)
Key Concept
Ratios compare quantities without units. They show the relationship between amounts.
What are Equivalent Ratios?
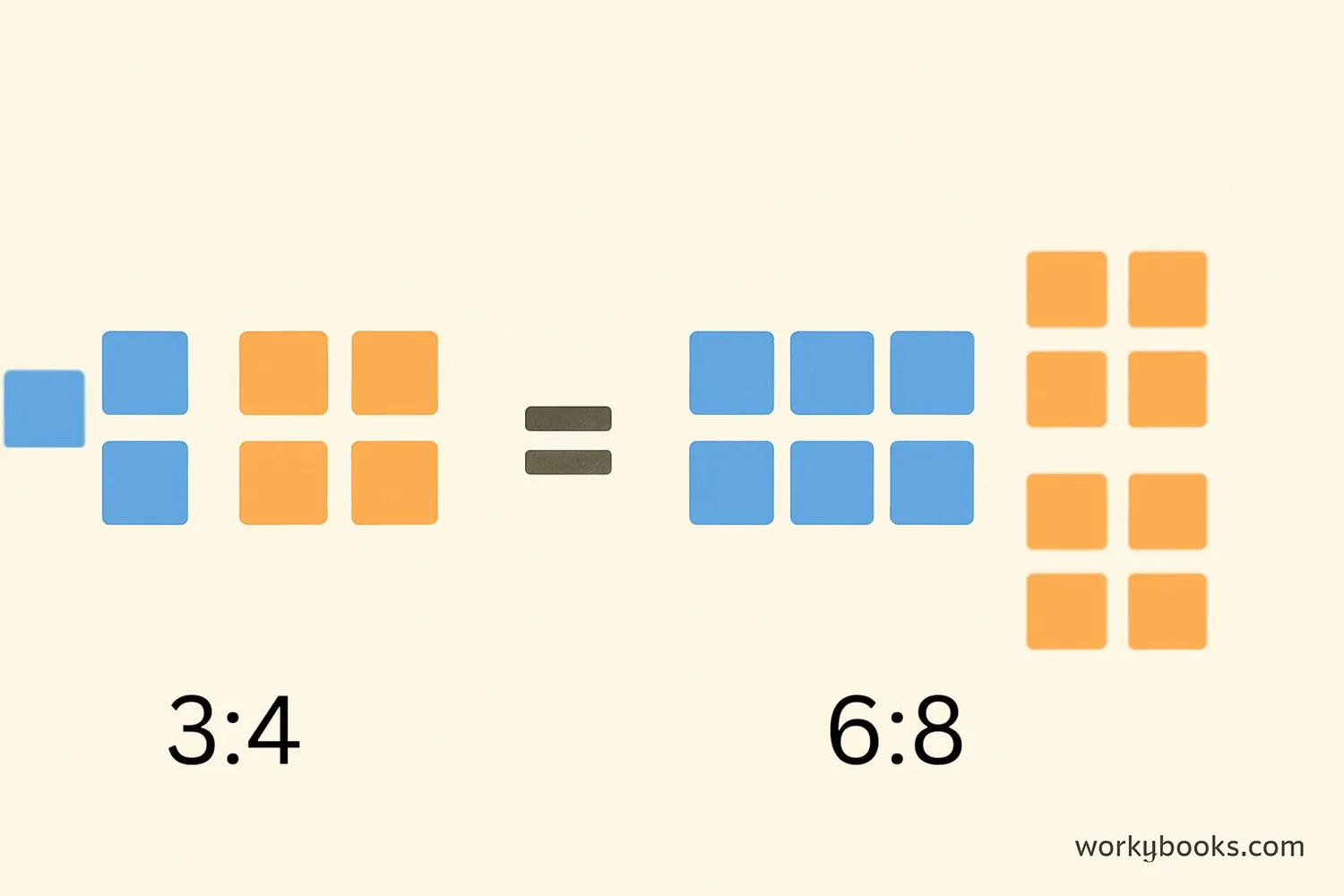
Equivalent ratios are different ratios that represent the same relationship between quantities. They are like different ways of expressing the same proportion.
For example, the ratio 2:3 is equivalent to 4:6 because both represent the same proportional relationship. If you double both numbers in 2:3, you get 4:6.
Think of equivalent ratios as fractions that have the same value. Just like 1/2 is equivalent to 2/4, ratios can be equivalent too!
Visualizing Equivalent Ratios
Remember
Equivalent ratios can be found by multiplying or dividing both terms by the same number.
How to Find Equivalent Ratios

There are two main ways to find equivalent ratios:
Multiplication Method
Multiply both terms of the ratio by the same number.
Division Method
Divide both terms of the ratio by the same number.
Important
You can multiply or divide by any number except zero. The number must be the same for both parts of the ratio.
Examples of Equivalent Ratios
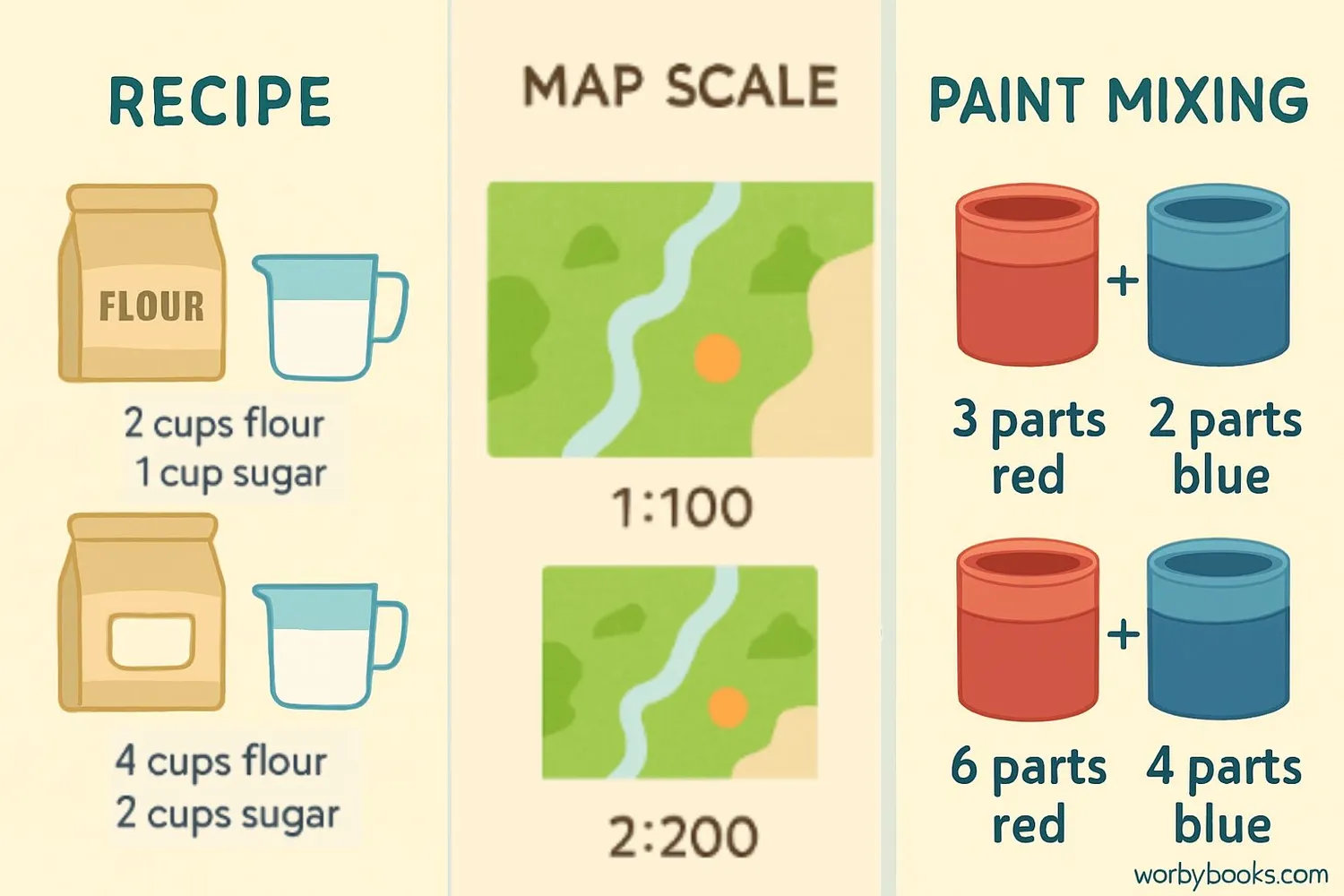
Let's look at some examples of equivalent ratios in different contexts:
Example 1: Recipe Scaling
A recipe calls for 2 cups of flour and 1 cup of sugar (ratio 2:1). If you want to make double the recipe, you'd use 4 cups of flour and 2 cups of sugar (ratio 4:2). The ratios 2:1 and 4:2 are equivalent.
Example 2: Map Scale
A map has a scale of 1 cm:10 km. This is equivalent to 2 cm:20 km and 5 cm:50 km. All represent the same proportional relationship between distance on the map and actual distance.
Example 3: Mixing Paint
To make purple paint, you mix 3 parts red with 2 parts blue (3:2). This is equivalent to 6 parts red and 4 parts blue (6:4) or 9 parts red and 6 parts blue (9:6). All these mixtures will produce the same shade of purple.
Example 4: Classroom Ratios
In a classroom, there are 4 girls for every 5 boys (4:5). If the class size doubles, there would be 8 girls for every 10 boys (8:10). The ratios 4:5 and 8:10 are equivalent.
Practice Tip
To check if two ratios are equivalent, divide the first number by the second number in each ratio. If you get the same decimal, they are equivalent!
Equivalent Ratios Practice Quiz
Test your understanding of equivalent ratios with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about equivalent ratios:
Math Trivia
Discover interesting facts about ratios and proportions:
Ancient Ratios
The concept of ratios dates back to ancient Egypt and Babylon. Egyptian architects used ratios to design pyramids, maintaining consistent proportions regardless of size.
Golden Ratio
The golden ratio (approximately 1.618:1) appears throughout nature - in seashells, flower petals, and even human body proportions. Artists and architects have used it for centuries for its pleasing proportions.
Scale Models
Scale models use ratios to represent real objects. A 1:24 scale model car means that 1 unit on the model equals 24 units on the real car. All dimensions maintain this proportional relationship.
Largest Ratio
The largest ratio ever calculated in mathematics is Graham's number, which is so large that the observable universe isn't big enough to write it down. It appears in solutions to certain problems in Ramsey theory.





