Expanded Form with Decimals - Definition, Examples, Quiz, FAQ, Trivia
Learn to write decimals in expanded form with place value understanding and practice activities
What is Expanded Form with Decimals?

Expanded form is a way to write numbers by showing the value of each digit. For decimals, we break down the number into each place value (ones, tenths, hundredths, etc.) and write it as a sum.
When we write numbers in expanded form with decimals, we're showing how much each digit contributes to the total value of the number. This helps us understand place value better and see how decimals relate to fractions.
For example, the decimal 3.25 can be written in expanded form as:
3 × 1 + 2 × 0.1 + 5 × 0.01 or 3 + 2/10 + 5/100
Key Concept
Expanded form shows the value of each digit in a number based on its place value position.
How to Write Decimals in Expanded Form

Converting decimals to expanded form follows these simple steps:
Step 1: Identify each digit in the decimal number
Step 2: Determine the place value of each digit
Step 3: Write each digit multiplied by its place value
Step 4: Express it as a sum of all the values
Conversion Formula
Multiply each digit by its place value, then add them together.
Example: Write 4.73 in expanded form
Step 1: Identify digits → 4, 7, 3
Step 2: Place values → ones (1), tenths (0.1), hundredths (0.01)
Step 3: Multiply → 4 × 1 + 7 × 0.1 + 3 × 0.01
Step 4: Expanded form → 4 + 0.7 + 0.03
We can also write it with fractions: 4 + 7/10 + 3/100
Remember
The decimal point separates the whole number part from the fractional part. To the left are ones, tens, hundreds. To the right are tenths, hundredths, thousandths.
Examples of Expanded Form with Decimals
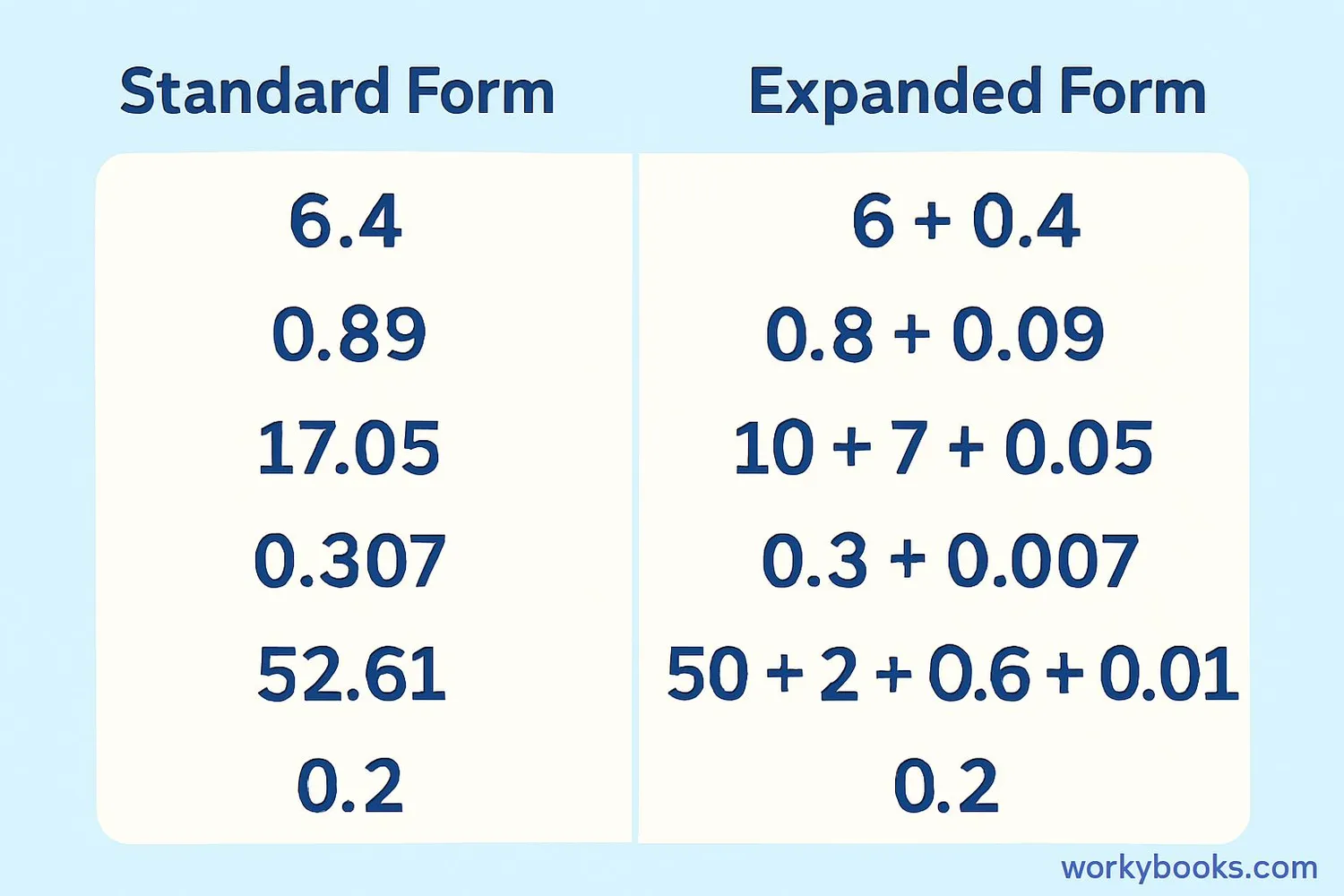
Let's look at more examples of writing decimals in expanded form:
Example 1: 2.6 = 2 × 1 + 6 × 0.1 = 2 + 0.6
Example 2: 0.45 = 4 × 0.1 + 5 × 0.01 = 0.4 + 0.05
Example 3: 9.108 = 9 × 1 + 1 × 0.1 + 0 × 0.01 + 8 × 0.001 = 9 + 0.1 + 0.008
Example 4: 13.72 = 10 + 3 + 0.7 + 0.02 = 1 × 10 + 3 × 1 + 7 × 0.1 + 2 × 0.01
We can also write these using fraction form:
2.6 = 2 + 6/10
0.45 = 4/10 + 5/100
9.108 = 9 + 1/10 + 8/1000
13.72 = 10 + 3 + 7/10 + 2/100
Practice Tip
Remember that zeros in decimal places are important placeholders. For example, in 2.05, the zero tells us there are no tenths.
Decimal Place Value Charts
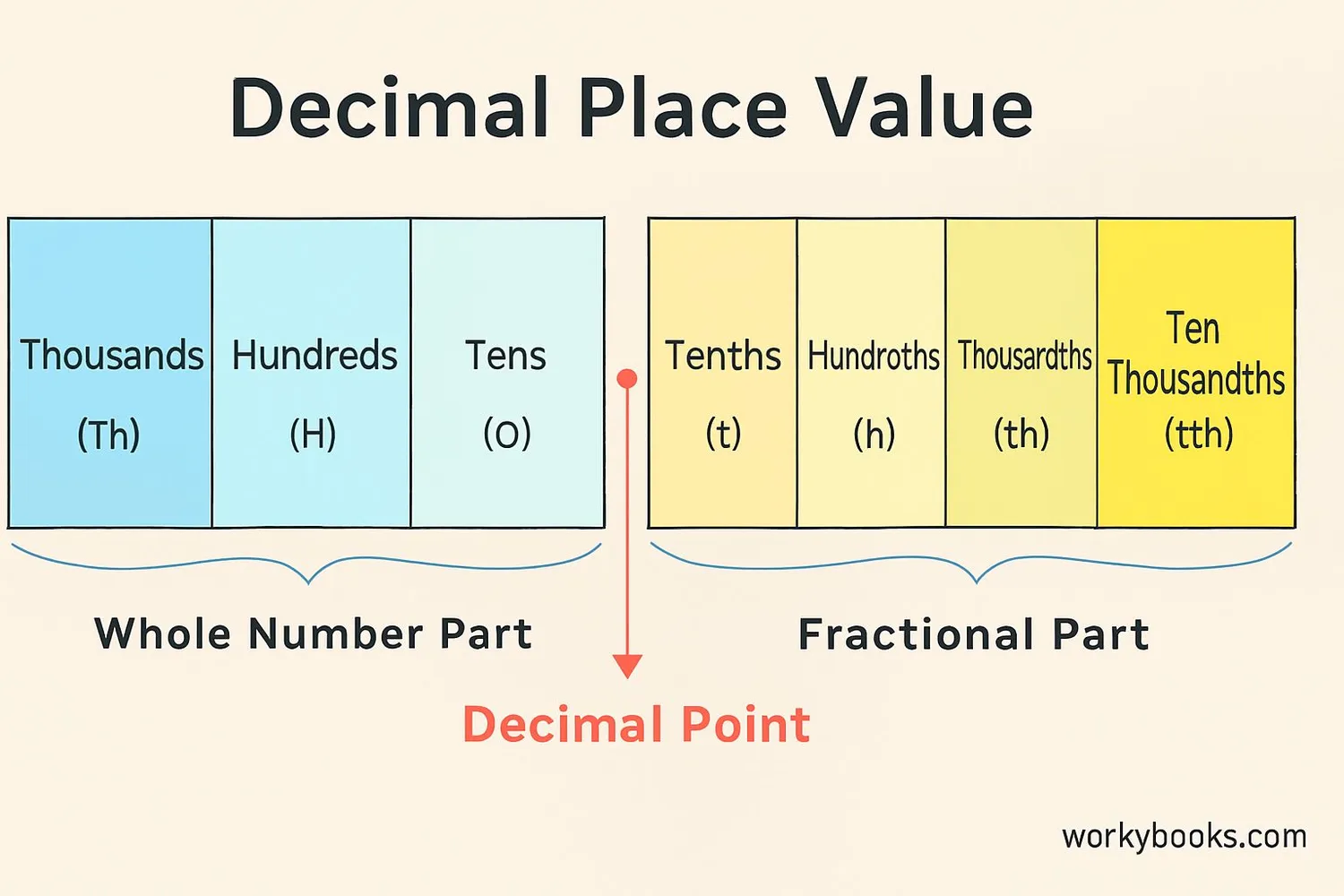
Place value charts help us understand the value of each digit in a decimal number. Here are useful charts for decimal place values:
Decimal Place Value Chart
| Place Value | Value | Fraction | Example (3.142) |
|---|---|---|---|
| Ones | 1 | 1 | 3 |
| Tenths | 0.1 | 1/10 | 1 |
| Hundredths | 0.01 | 1/100 | 4 |
| Thousandths | 0.001 | 1/1000 | 2 |
| Ten-Thousandths | 0.0001 | 1/10000 | - |
Expanded Form Examples Chart
| Standard Form | Expanded Form (Decimals) | Expanded Form (Fractions) |
|---|---|---|
| 0.7 | 7 × 0.1 | 7/10 |
| 0.25 | 2 × 0.1 + 5 × 0.01 | 2/10 + 5/100 |
| 1.3 | 1 × 1 + 3 × 0.1 | 1 + 3/10 |
| 2.06 | 2 × 1 + 6 × 0.01 | 2 + 6/100 |
| 4.125 | 4 × 1 + 1 × 0.1 + 2 × 0.01 + 5 × 0.001 | 4 + 1/10 + 2/100 + 5/1000 |
Chart Tip
Notice how each place to the right of the decimal point is 10 times smaller than the place to its left.
Expanded Form Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about expanded form with decimals:
Math Trivia
Discover interesting facts about decimals and number systems:
Decimal History
The decimal system was developed by many ancient civilizations, but the modern decimal notation with a point was popularized by Scottish mathematician John Napier in the early 17th century.
Global Decimals
While most countries use a decimal point (.), some European countries use a comma (,) instead. For example, 3.14 in the US is written as 3,14 in many European countries.
Precision Matters
In scientific measurements, decimal place value is crucial. The 1999 Mars Climate Orbiter was lost because of a unit conversion error between metric and imperial measurements.
Infinite Decimals
Some decimals go on forever without repeating! Pi (π) is a famous example - it starts with 3.14159 but continues infinitely without repeating pattern.





