Factors and Multiples - Definition, Examples, Quiz, FAQ, Trivia
Learn about factors, multiples, prime numbers, and more with easy explanations and practice activities
What Are Factors and Multiples?

Factors are numbers we multiply together to get another number. For example, the factors of 12 are 1, 2, 3, 4, 6, and 12 because:
1 × 12 = 12
2 × 6 = 12
3 × 4 = 12
Multiples are what we get after multiplying a number by other whole numbers. For example, the multiples of 3 are 3, 6, 9, 12, 15, and so on.
Think of factors as numbers that divide evenly into another number, and multiples as the result of multiplying a number by 1, 2, 3, and so on.
Example
Find the factors of 18:
1 × 18 = 18
2 × 9 = 18
3 × 6 = 18
So the factors of 18 are: 1, 2, 3, 6, 9, 18
Key Concept
Factors are the numbers that divide exactly into another number. Multiples are the results of multiplying a number by other whole numbers.
Prime and Composite Numbers

Prime numbers are special numbers that have exactly two factors: 1 and themselves. The number 1 is not considered prime because it only has one factor.
Examples of prime numbers: 2, 3, 5, 7, 11, 13, 17, 19, 23...
Composite numbers have more than two factors. This means they can be divided evenly by numbers other than just 1 and themselves.
Examples of composite numbers: 4, 6, 8, 9, 10, 12, 14, 15, 16...
The number 1 is neither prime nor composite because it has only one factor.
Example
Is 17 a prime number?
The factors of 17 are only 1 and 17. So yes, 17 is prime.
Is 15 a prime number?
The factors of 15 are 1, 3, 5, and 15. So 15 is composite.
Remember
Prime numbers have exactly two factors. Composite numbers have more than two factors.
Greatest Common Factor (GCF)

The Greatest Common Factor (GCF) of two or more numbers is the largest number that divides evenly into all of them.
To find the GCF:
1. List all the factors of each number
2. Identify the common factors
3. Choose the largest of these common factors
The GCF is useful for simplifying fractions and solving problems about equal grouping or dividing things evenly.
Example
Find the GCF of 12 and 18:
Factors of 12: 1, 2, 3, 4, 6, 12
Factors of 18: 1, 2, 3, 6, 9, 18
Common factors: 1, 2, 3, 6
The greatest common factor is 6.
Tip
You can also find the GCF by multiplying the common prime factors of the numbers.
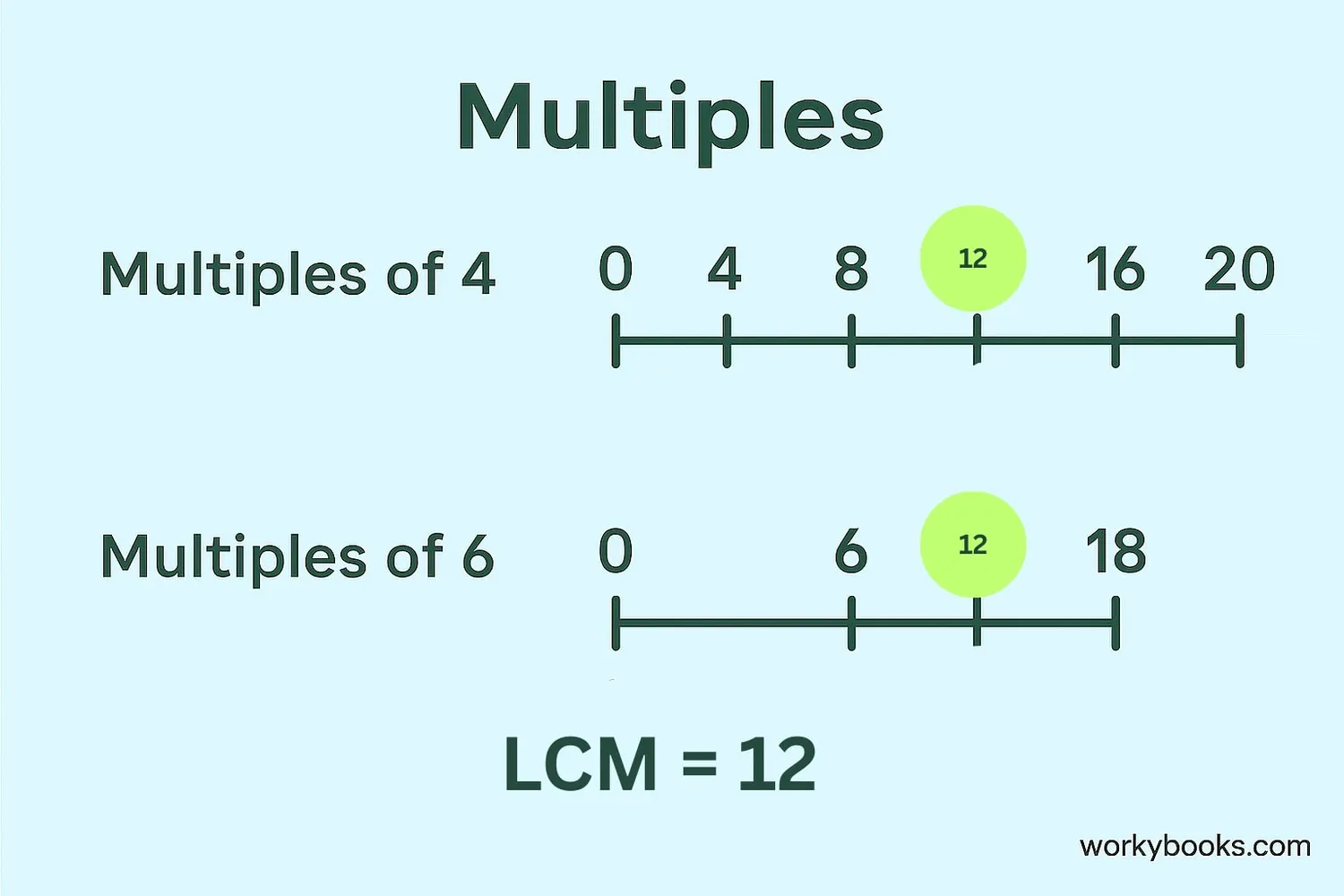
Least Common Multiple (LCM)
The Least Common Multiple (LCM) of two or more numbers is the smallest number that is a multiple of all of them.
To find the LCM:
1. List the first several multiples of each number
2. Identify the common multiples
3. Choose the smallest of these common multiples
The LCM is useful for finding common denominators in fractions and solving problems about events happening at the same time.
Example
Find the LCM of 4 and 6:
Multiples of 4: 4, 8, 12, 16, 20, 24...
Multiples of 6: 6, 12, 18, 24, 30...
Common multiples: 12, 24...
The least common multiple is 12.
Remember
The LCM is always at least as large as the largest number in your set.
Prime Factorization
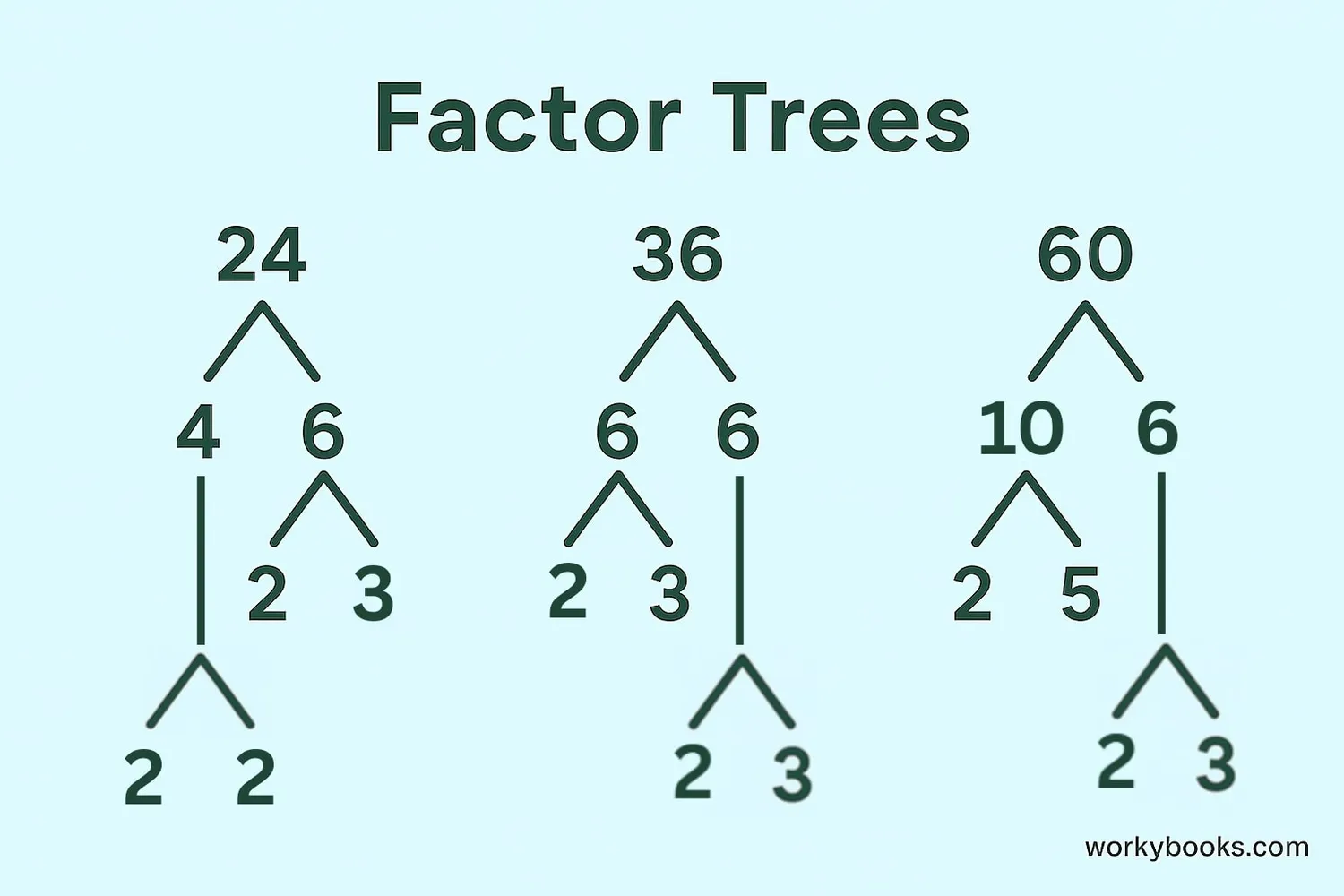
Prime factorization is breaking down a composite number into its prime factors. This means we express the number as a product of prime numbers.
We often use factor trees to find prime factors:
1. Start with the number at the top
2. Find two factors that multiply to make that number
3. Continue breaking down composite factors until all factors are prime
Prime factorization is useful for finding the GCF and LCM of numbers, especially larger numbers.
Example
Find the prime factorization of 24:
24 = 2 × 12
12 = 2 × 6
6 = 2 × 3
So the prime factorization of 24 is 2 × 2 × 2 × 3, or 2³ × 3.
Key Concept
Every composite number can be written as a unique product of prime factors.
Factors and Multiples Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about factors and multiples:
Math Trivia
Discover interesting facts about numbers and mathematics:
Ancient Number Theory
The study of factors and multiples dates back to ancient Greek mathematicians. Euclid's "Elements," written around 300 BCE, contains important theorems about prime numbers and divisibility.
Prime Numbers in Nature
Some cicada species emerge in prime-numbered year cycles (13 or 17 years). Scientists believe this helps them avoid predators with shorter life cycles, as their emergence rarely syncs up with predator population peaks.
Largest Known Prime
The largest known prime number (as of 2023) has over 24 million digits! It was discovered through the Great Internet Mersenne Prime Search (GIMPS), a collaborative project of volunteers using their computers.
Perfect Numbers
A perfect number equals the sum of its proper factors. For example, 6 (1+2+3=6) and 28 (1+2+4+7+14=28) are perfect numbers. Euclid discovered that if 2^p-1 is prime, then (2^p-1)×2^(p-1) is a perfect number.





