Fibonacci Numbers - Definition, Examples, Quiz, FAQ, Trivia
Discover the amazing mathematical pattern found in nature, art, and science
What is the Fibonacci Sequence?

The Fibonacci sequence is a special pattern of numbers that starts with 0 and 1, and each following number is the sum of the two numbers before it.
Here's how it begins:
This sequence is named after Leonardo Fibonacci, an Italian mathematician who lived over 800 years ago. He discovered this pattern while studying rabbit populations.
Fibonacci numbers appear everywhere in nature - in the arrangement of leaves on a stem, the pattern of seeds in a sunflower, and the spiral of a seashell!
Key Concept
The Fibonacci sequence starts with 0 and 1, and each number after that is the sum of the two numbers before it.
Fibonacci Formula & Golden Ratio
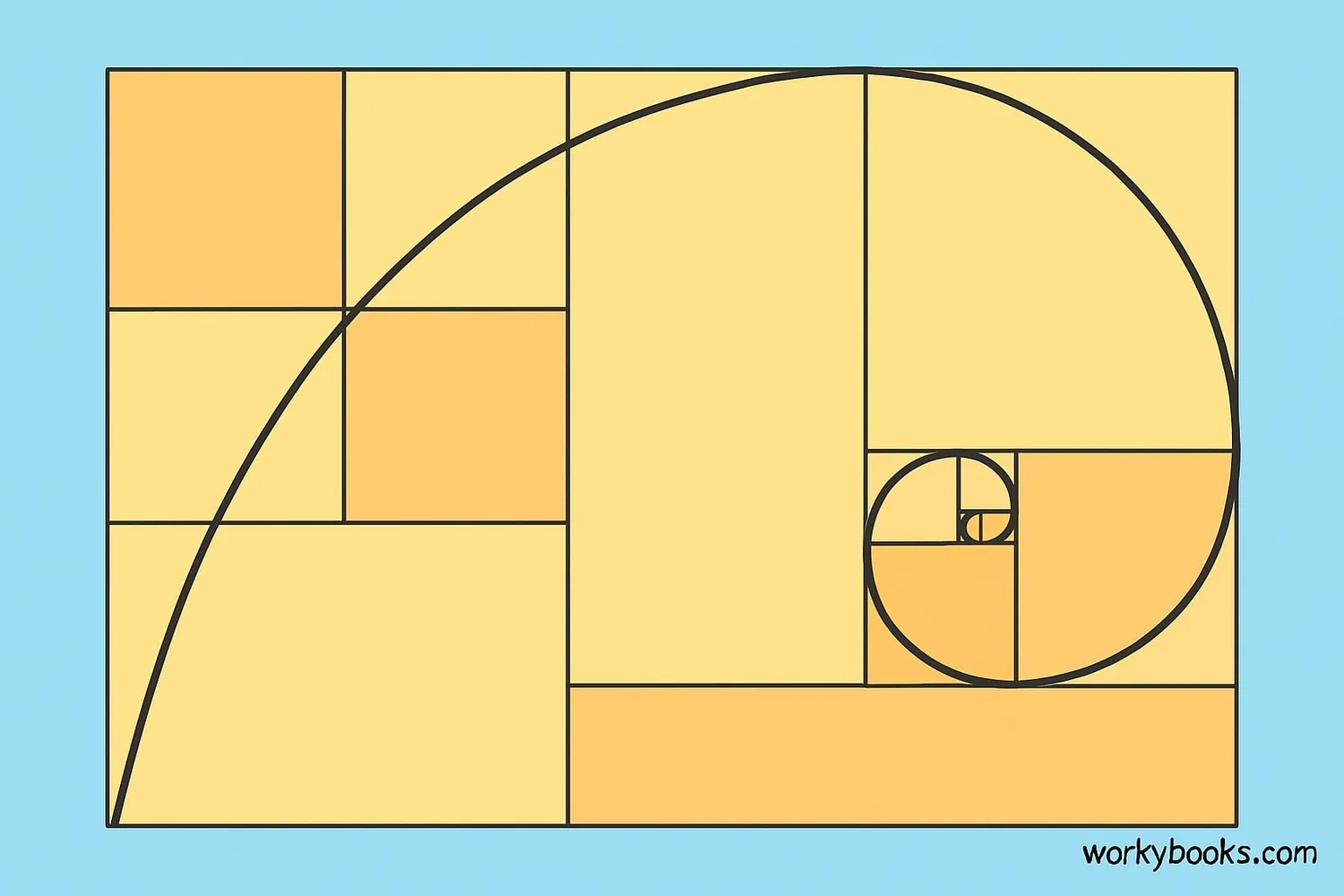
The Fibonacci sequence follows a simple mathematical rule:
Fibonacci Formula
Where F(n) is the current number, F(n-1) is the previous number, and F(n-2) is the number before that.
When you divide a Fibonacci number by the one before it, the result gets closer and closer to the Golden Ratio as the numbers get larger:
| Fibonacci Numbers | Division | Result |
|---|---|---|
| 3 ÷ 2 | 3/2 | 1.5 |
| 5 ÷ 3 | 5/3 | ≈1.666 |
| 8 ÷ 5 | 8/5 | 1.6 |
| 13 ÷ 8 | 13/8 | 1.625 |
| 21 ÷ 13 | 21/13 | ≈1.615 |
| 34 ÷ 21 | 34/21 | ≈1.619 |
The Golden Ratio is found in art, architecture, and throughout nature because many people find it visually pleasing.
Remember
The ratio between consecutive Fibonacci numbers approaches the Golden Ratio (≈1.618) as the numbers get larger.
Properties of Fibonacci Numbers

Fibonacci numbers have many interesting mathematical properties:
1. Every 3rd Fibonacci number is even:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144...
2. The sum of the first n Fibonacci numbers:
F1 + F2 + ... + Fn = Fn+2 - 1
3. Consecutive Fibonacci numbers are coprime:
They have no common factors other than 1. For example, 8 and 13 (factors: 2×2×2 and 13).
4. The difference of squares:
Fn+1 × Fn-1 - Fn2 = (-1)n
These patterns show how special the Fibonacci sequence is in mathematics!
Pattern Tip
Look for Fibonacci numbers in flower petals - many have 3, 5, 8, 13 or 21 petals!
Applications of Fibonacci Numbers
Fibonacci numbers aren't just mathematical curiosities - they have real-world applications:
1. Nature: The arrangement of leaves around a stem, the spiral patterns in pinecones and sunflowers, and the branching patterns of trees all follow Fibonacci sequences.
2. Computer Science: The Fibonacci search technique helps computers find items in sorted lists quickly. Fibonacci heaps are special data structures used in computer algorithms.
3. Art and Architecture: Many artists and architects use the Golden Ratio (related to Fibonacci numbers) in their designs. The Parthenon in Greece and the pyramids in Egypt both use these proportions.
4. Finance: Stock market analysts sometimes use Fibonacci numbers to predict where prices might change direction.
5. Music: Musical scales and the arrangement of notes often follow Fibonacci patterns. Some pianos have 13 keys in an octave (8 white, 5 black) - both Fibonacci numbers!
Application Tip
Look for Fibonacci numbers in fruits and vegetables - pineapples have spirals with 8, 13, and 21 rows!
Fibonacci and Pascal's Triangle
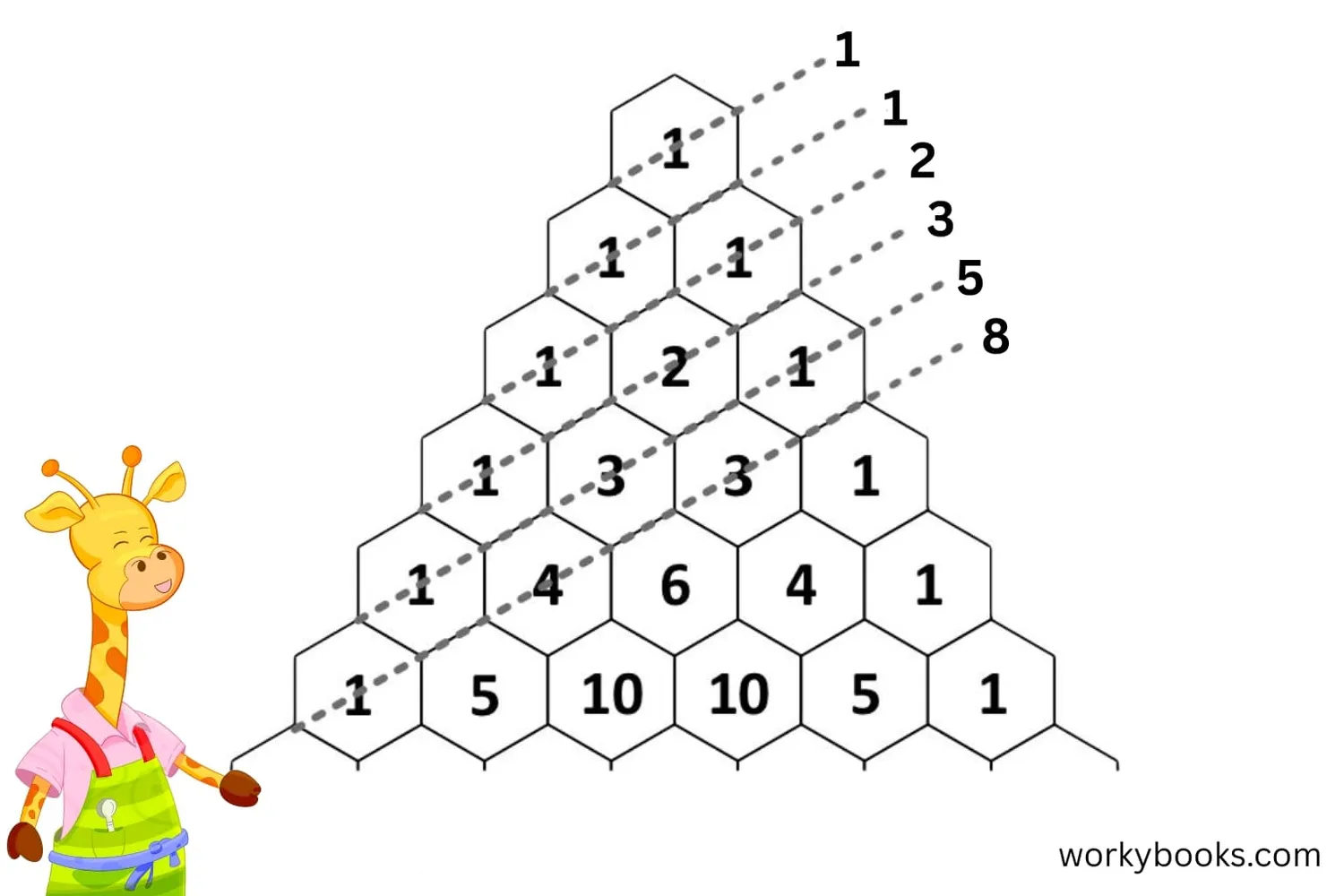
Pascal's Triangle is a triangular arrangement of numbers where each number is the sum of the two numbers above it. Amazingly, it contains the Fibonacci sequence!
If you add the numbers along the diagonal lines in Pascal's Triangle, you get the Fibonacci sequence:
| Diagonal Sum | Result | Fibonacci Number |
|---|---|---|
| 1st diagonal | 1 | F1 |
| 2nd diagonal | 1 | F2 |
| 3rd diagonal | 1+1=2 | F3 |
| 4th diagonal | 1+2=3 | F4 |
| 5th diagonal | 1+3+1=5 | F5 |
| 6th diagonal | 1+4+3=8 | F6 |
This is just one example of how the Fibonacci sequence appears in different areas of mathematics. The connections between these mathematical concepts show how beautifully mathematics fits together!
Math Connection
Pascal's Triangle also contains many other number sequences like triangular numbers and powers of 2.
Fibonacci Numbers Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about Fibonacci numbers:
Math Trivia
Discover interesting facts about Fibonacci numbers:
Fibonacci's Real Name
Leonardo Fibonacci's real name was Leonardo of Pisa. "Fibonacci" means "son of Bonacci" and was a nickname given to him centuries after his death.
Nature's Favorite Numbers
Most daisies have 34, 55, or 89 petals - all Fibonacci numbers! This arrangement allows for optimal packing of seeds and exposure to sunlight.
Art and Architecture
Leonardo da Vinci used the Golden Ratio (related to Fibonacci) in many paintings, including the Mona Lisa. The Parthenon's proportions also follow this ratio.
Huge Fibonacci Numbers
The largest known Fibonacci number has over 2 million digits! It would take about 500 pages to write out completely.





