Fractions vs Rational Numbers - Definition, Examples, Quiz, FAQ, Trivia
Learn the difference with simple explanations, visual examples, and practice activities
What is a Fraction?
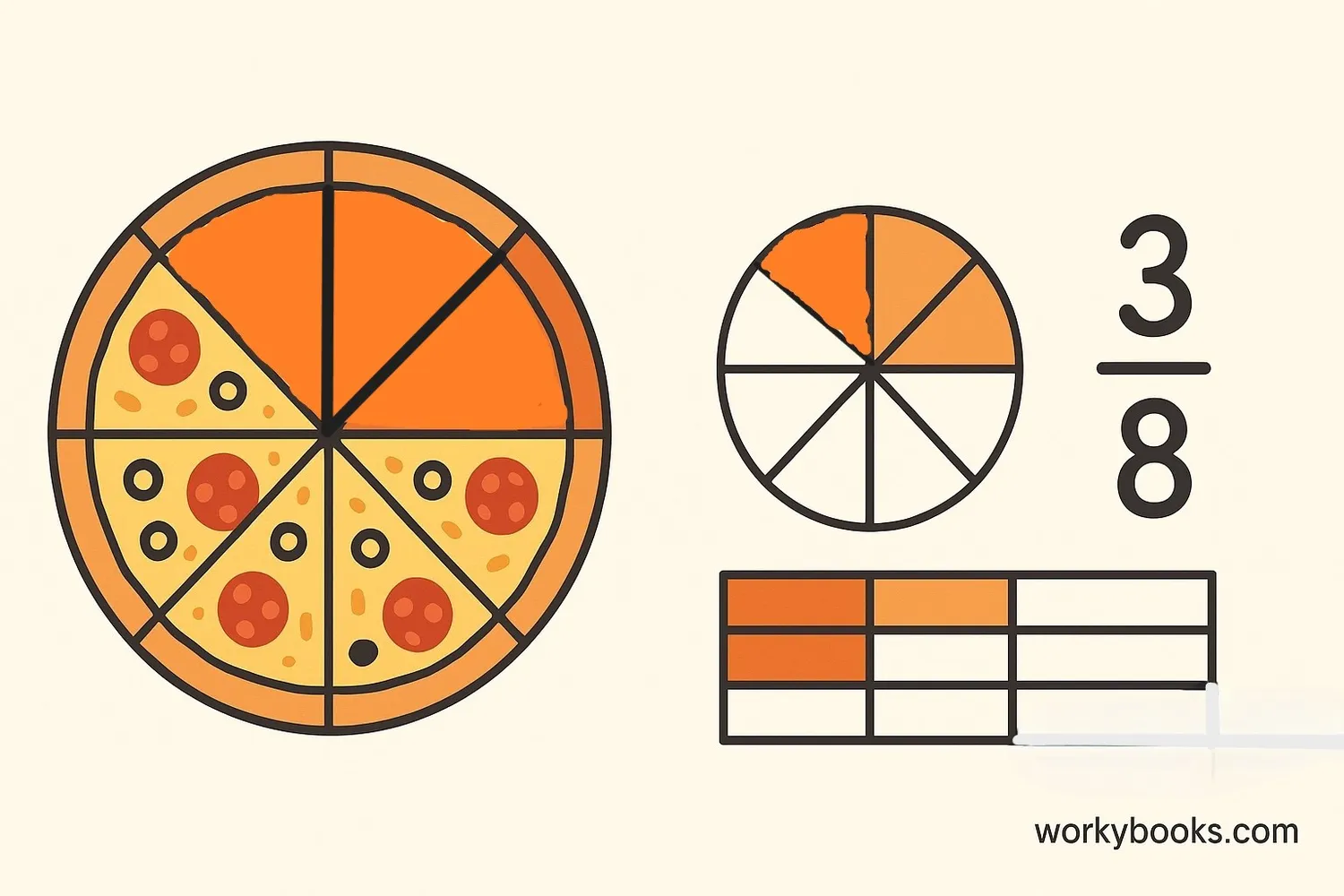
A fraction represents parts of a whole. When we divide something into equal pieces, a fraction shows how many of those pieces we have.
Fractions have two parts:
- The numerator (top number) tells how many parts we have
- The denominator (bottom number) tells how many equal parts the whole is divided into
For example, in the fraction ¾:
- Numerator is 3 (we have 3 parts)
- Denominator is 4 (the whole is divided into 4 equal parts)
Fractions must have positive integers for both numerator and denominator. The denominator can never be zero!
Key Concept
Fractions represent parts of a whole and must have positive integers for both numerator and denominator.
What is a Rational Number?
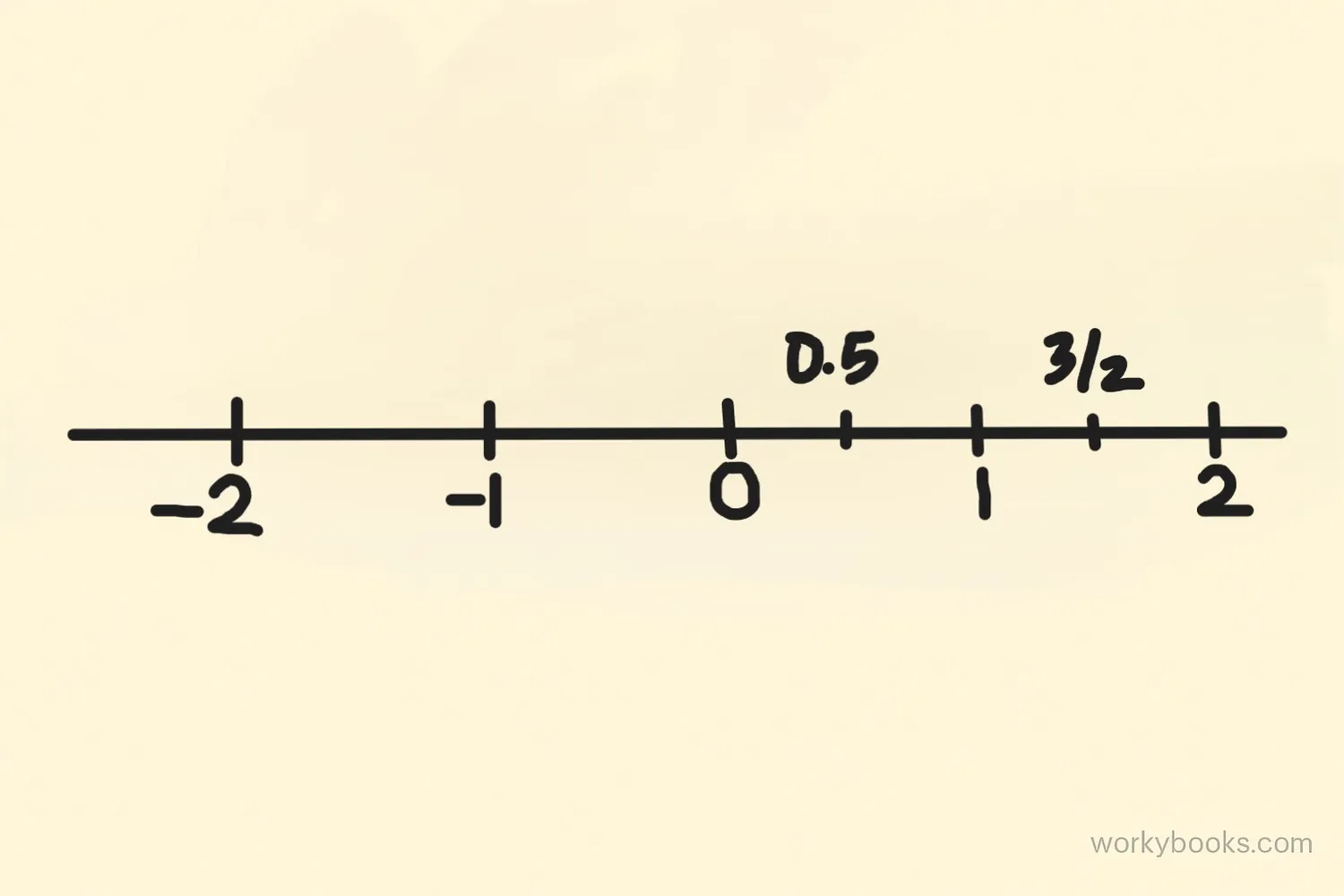
Rational numbers are numbers that can be expressed as a ratio of two integers, where the denominator is not zero.
This means:
- They can be written as a fraction (like 3/4)
- They can be positive or negative (like -2/3)
- They include whole numbers (like 5 = 5/1)
- They include integers (like -3 = -3/1)
The general form of a rational number is a/b where:
- a and b are integers
- b is not zero
Rational Number Definition
Any number that can be expressed as a ratio of two integers
Remember
All fractions are rational numbers, but not all rational numbers are fractions!
Key Differences
While all fractions are rational numbers, there are important differences:
| Characteristic | Fractions | Rational Numbers |
|---|---|---|
| Definition | Parts of a whole | Ratio of two integers |
| Numerator | Positive integer | Any integer |
| Denominator | Positive integer | Any integer except zero |
| Can be negative? | No | Yes |
| Includes whole numbers? | Only when denominator is 1 | Yes (e.g., 5 = 5/1) |
| Includes integers? | Only positive integers | All integers (positive and negative) |
| Examples | 1/2, 3/4, 5/8 | 1/2, -3/4, 5, -2, 0.75 |
Quick Tip
If you see a negative sign in a fraction, it's a rational number but not a fraction. Fractions are always positive!
Examples
Let's look at some examples to understand the difference:
Example 1: 2/3
- This is both a fraction and a rational number
- It has positive integers for both numerator and denominator
Example 2: -5/8
- This is a rational number because it's a ratio of integers
- But it's not a fraction because fractions can't be negative
Example 3: 4 (which is 4/1)
- This is a rational number (can be written as 4/1)
- It's also a fraction because 4/1 has positive integers
Example 4: 0.6 (which is 3/5)
- This is a rational number because it can be written as 3/5
- It's also a fraction because 3/5 has positive integers
Remember
A number is rational if it can be expressed as a ratio of two integers. A fraction is specifically a ratio of two positive integers.
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about fractions and rational numbers:
Math Trivia
Discover interesting facts about numbers and mathematics:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They had special symbols for fractions like 1/2, 1/3, and 1/4, and represented other fractions as sums of these unit fractions.
Rational Numbers in Nature
Many patterns in nature follow rational numbers. The Fibonacci sequence (1, 1, 2, 3, 5, 8, 13...) creates ratios that approach the golden ratio, which is an irrational number approximately equal to 1.618.
Rational Numbers in Space
Astronomers use rational numbers to calculate distances between planets. For example, the ratio of Earth's distance from the Sun to Mars' distance is about 1.5, which is the rational number 3/2.
Largest Denominator
The fraction with the largest denominator commonly used in mathematics is the "googolplex," which is 1 followed by a googol of zeros. A googol is 10100 - that's 1 followed by 100 zeros!





