Height of Equilateral Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about triangle measurements with easy explanations, formulas, and practice activities
What is an Equilateral Triangle?
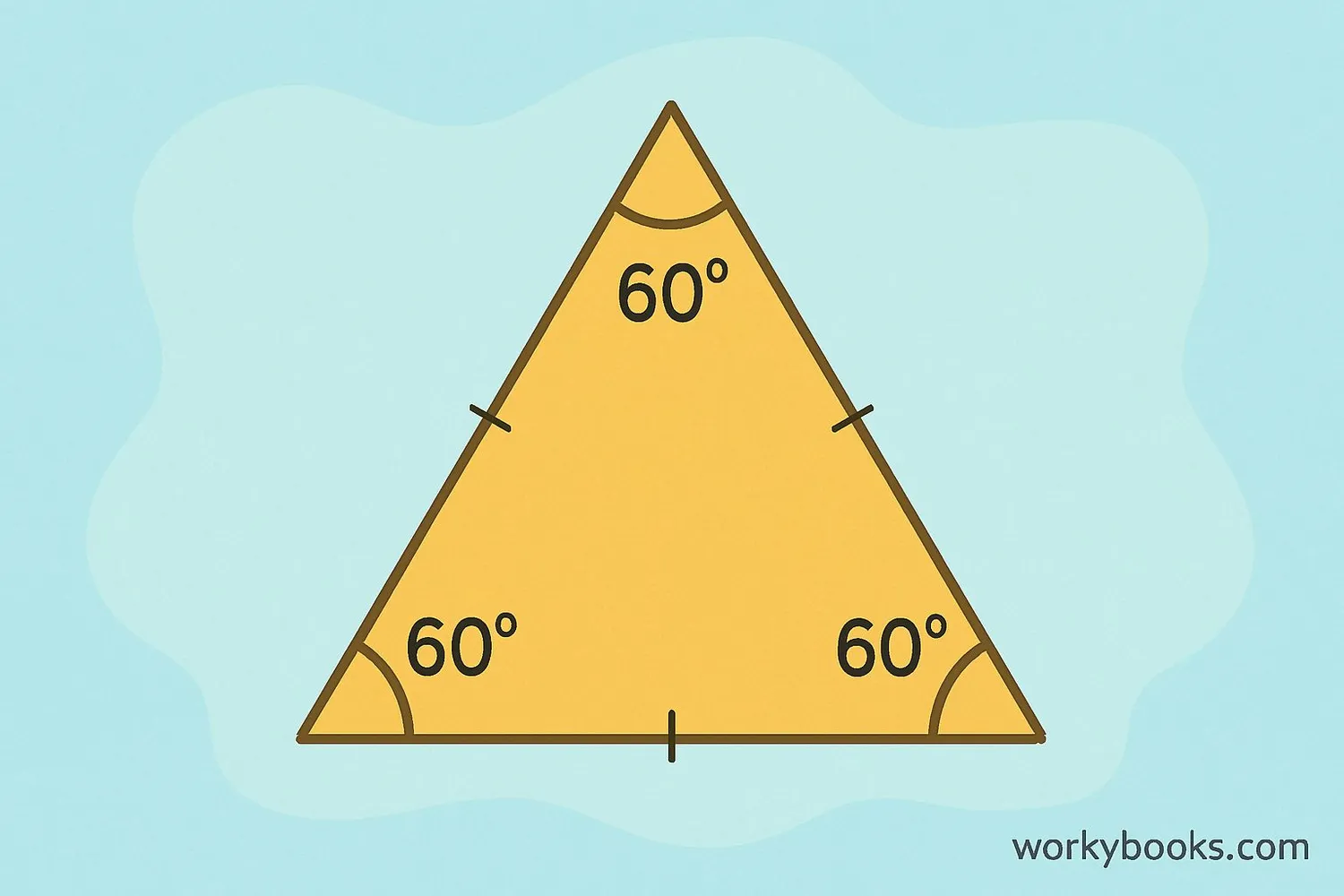
An equilateral triangle is a special type of triangle where all three sides are exactly the same length, and all three angles are equal to 60 degrees. The word "equilateral" comes from Latin: "equi" means equal, and "lateral" means sides.
The height of an equilateral triangle (also called its altitude) is a line segment drawn from any vertex perpendicular to the opposite side. This height divides the equilateral triangle into two equal right triangles, which helps us calculate its measurement using math formulas.
Understanding the height of triangles is important in geometry and has real-world applications in construction, engineering, and design.
Key Concept
In an equilateral triangle, all sides are equal, all angles are 60°, and the height divides the triangle into two congruent right triangles.
Height of Equilateral Triangle Formula
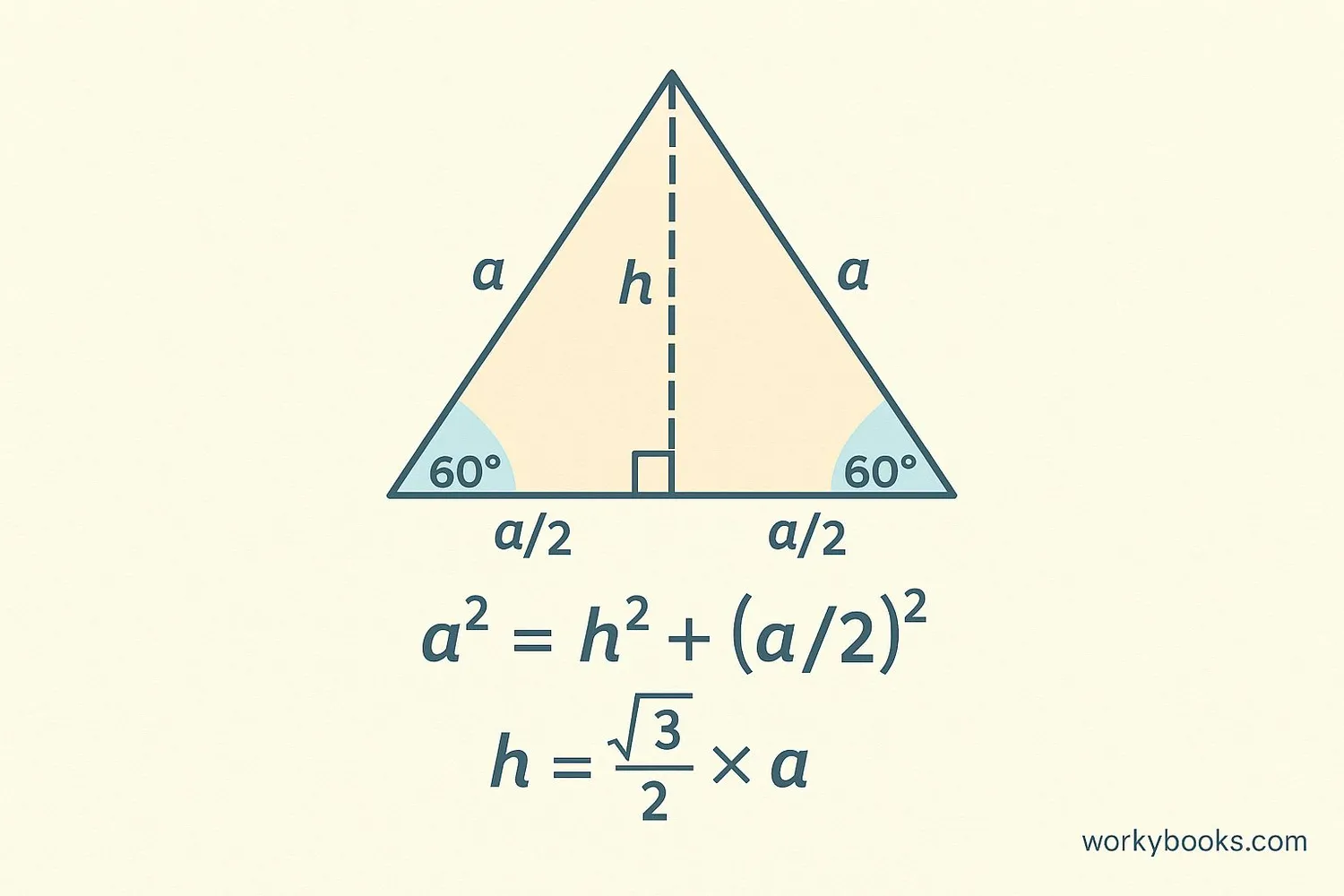
To find the height of an equilateral triangle, we use a special formula that relates the height to the side length. When we draw the height, it splits the equilateral triangle into two identical right triangles with angles of 30°, 60°, and 90°.
Height Formula
Where h is the height and a is the length of one side of the equilateral triangle.
When the height is drawn, it divides the base into two equal parts, each measuring a/2. Using the Pythagorean theorem on one of the right triangles:
a² = h² + (a/2)²
Solving for h: h² = a² - (a/2)² = a² - a²/4 = (3a²)/4
Therefore: h = √(3a²/4) = (√3/2) × a
Steps to Find the Height
Remember
The height of an equilateral triangle is always shorter than its sides because √3/2 is approximately 0.866, which is less than 1.
Examples
Let's practice using the height formula with some examples:
Example 1: Find the height of an equilateral triangle with side length 6 cm.
Solution: h = (√3/2) × a = (√3/2) × 6 = 3√3 ≈ 5.196 cm
Example 2: An equilateral triangle has a side length of 10 inches. What is its height?
Solution: h = (√3/2) × 10 = 5√3 ≈ 8.66 inches
Example 3: If the height of an equilateral triangle is 8.66 units, what is its side length?
Solution: From h = (√3/2) × a, we get a = (2/√3) × h
a = (2/√3) × 8.66 ≈ (1.1547) × 8.66 ≈ 10 units
Example 4: A triangular garden has equal sides of 12 feet. How tall is it at the center?
Solution: h = (√3/2) × 12 = 6√3 ≈ 10.392 feet
Common Height Values
| Side Length | Height | Approximate Height |
|---|---|---|
| 2 units | √3 units | 1.732 units |
| 4 units | 2√3 units | 3.464 units |
| 6 units | 3√3 units | 5.196 units |
| 8 units | 4√3 units | 6.928 units |
| 10 units | 5√3 units | 8.66 units |
| 12 units | 6√3 units | 10.392 units |
Practice Tip
Notice the pattern: height = side length × 0.866. You can use this approximation for quick calculations!
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about equilateral triangles and their height:
Geometry Trivia
Discover interesting facts about triangles and geometry:
Ancient Geometry
The ancient Egyptians used triangles and their properties in building the pyramids. They understood practical geometry long before the formal mathematical principles were established.
Triangular Numbers
Triangular numbers are numbers that can form an equilateral triangle. The sequence goes 1, 3, 6, 10, 15, 21... where each number represents dots that can be arranged in a triangle.
Triangles in Nature
Equilateral triangles appear in nature, including in honeycombs made by bees, certain crystal formations, and the arrangement of some flower petals. Their structural strength makes them efficient shapes.
Structural Strength
Triangles are the strongest geometric shape because they distribute weight evenly. This is why you see triangular shapes in bridges, towers, and roof trusses where strength is important.





