Inequalities - Definition, Examples, Quiz, FAQ, Trivia
Learn about math inequalities with easy explanations, examples, and practice activities
What is an Inequality?

An inequality in math is a statement that compares two values, showing that one value is greater than, less than, or not equal to another value.
Unlike equations where both sides are equal (like 2 + 3 = 5), inequalities show that the two sides are not equal. For example, 4 > 3 means "4 is greater than 3" and 2 < 5 means "2 is less than 5."
We use inequalities in everyday life too! When we say "I have more than 5 marbles" or "This bag holds less than 10 books," we're using inequalities without the math symbols.
Key Concept
Inequalities show relationships between values that are not equal. They use special symbols like >, <, ≥, ≤, and ≠.
Inequality Signs and Symbols
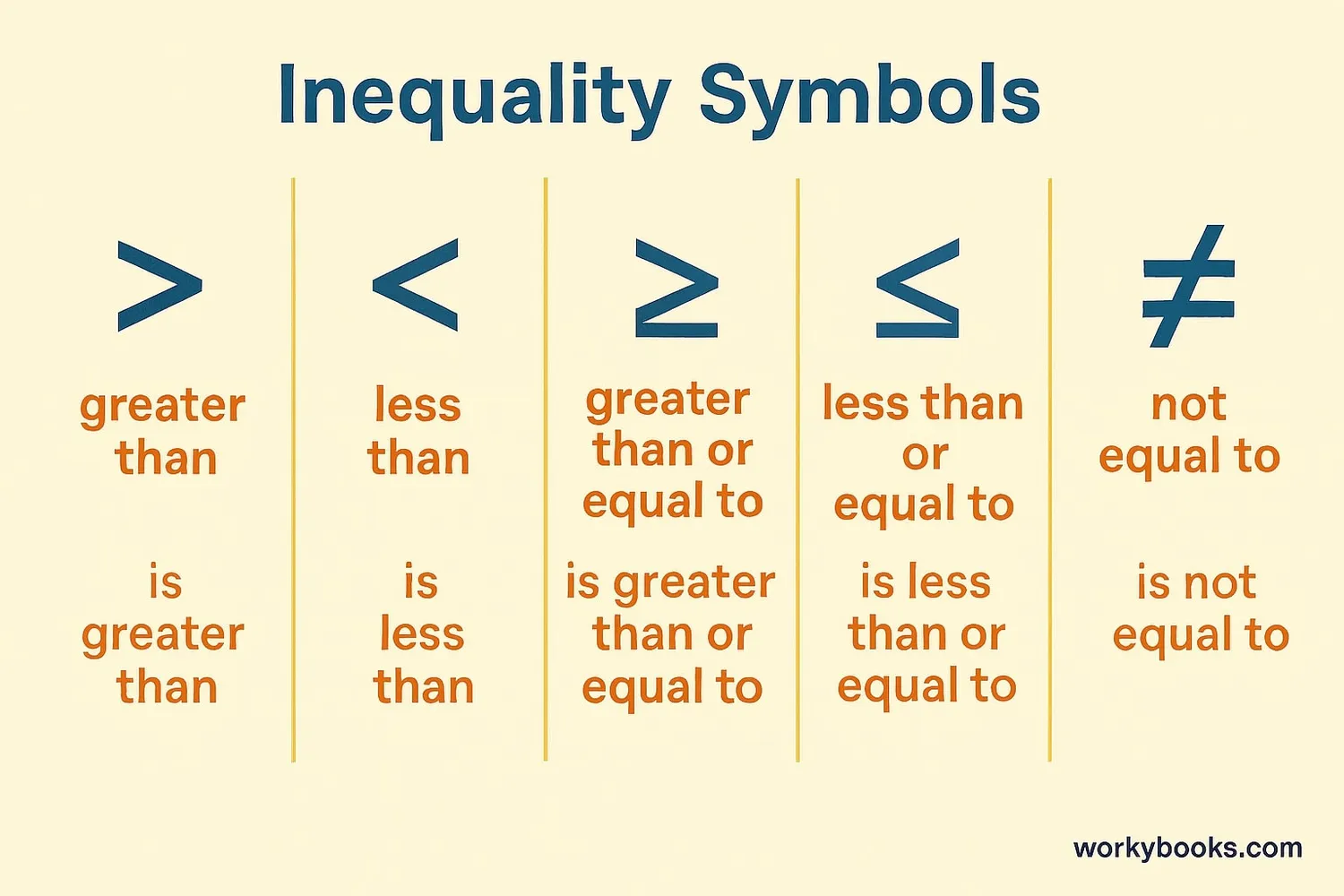
Math uses special symbols to show inequalities. Here are the main inequality symbols:
| Symbol | Name | Meaning | Example |
|---|---|---|---|
| > | Greater than | The value on the left is larger | 7 > 3 |
| < | Less than | The value on the left is smaller | 2 < 9 |
| ≥ | Greater than or equal to | The value on the left is larger or equal | x ≥ 5 |
| ≤ | Less than or equal to | The value on the left is smaller or equal | y ≤ 10 |
| ≠ | Not equal to | The values are different | 4 ≠ 7 |
Remembering the Symbols
Think of the inequality sign as a hungry alligator's mouth. The alligator always wants to eat the bigger number! For example, in 8 > 3, the alligator is eating the 8 because it's bigger.
Remember
The pointed end of the inequality symbol always faces the smaller value, and the open end faces the larger value.
Solving Inequalities
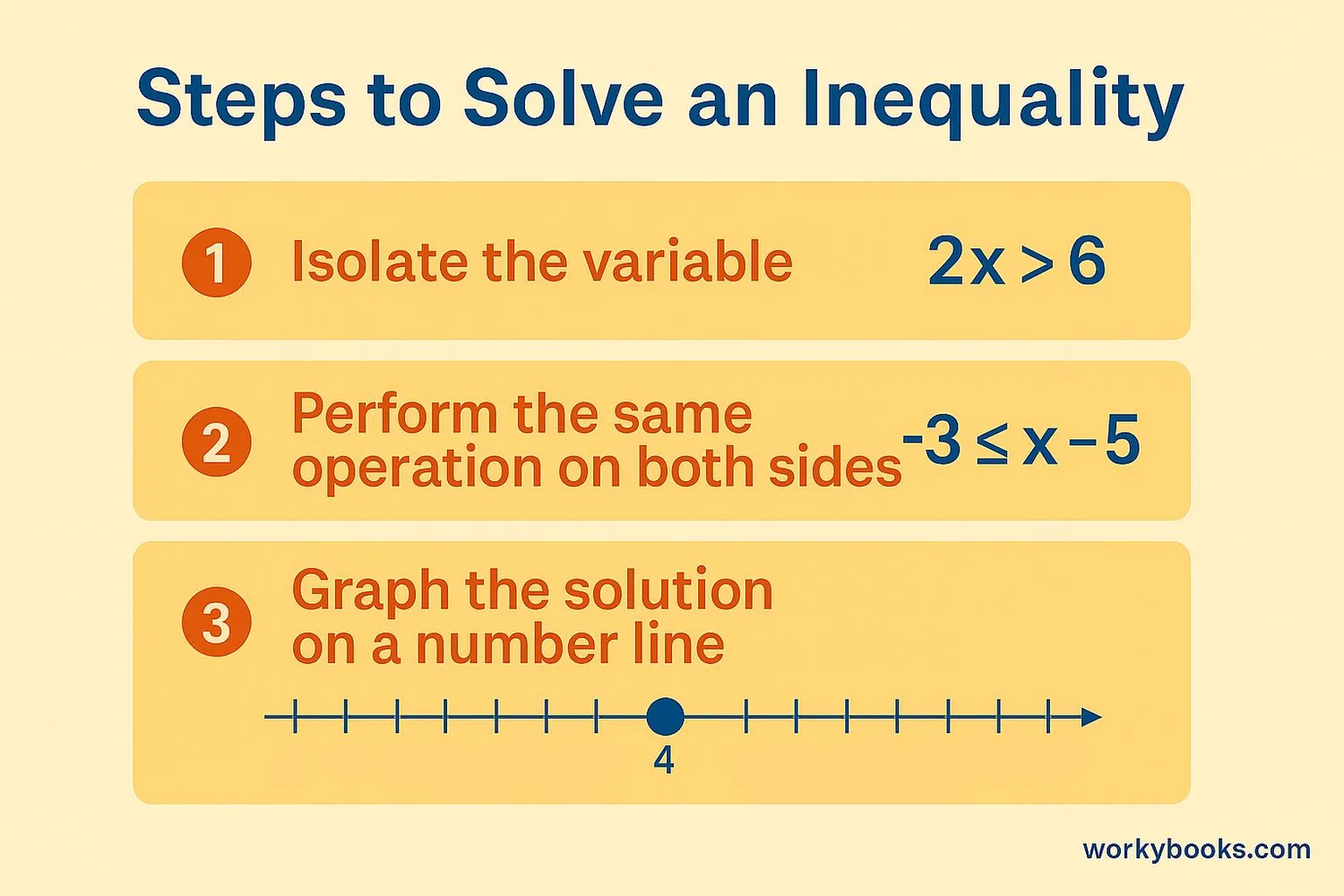
Solving inequalities is similar to solving equations, but with one important difference. When we multiply or divide both sides of an inequality by a negative number, we must flip the inequality sign!
Let's look at the steps to solve inequalities:
Simple Inequalities
Solve: x + 3 > 7
Subtract 3 from both sides: x > 4
This means x can be any number greater than 4.
With Multiplication
Solve: 2x ≤ 10
Divide both sides by 2: x ≤ 5
x can be 5 or any number less than 5.
Flipping the Sign
Solve: -3x < 6
Divide both sides by -3 (and flip the sign!): x > -2
When dividing by a negative, we flip the inequality sign.
Important Rule
This is the key difference between solving equations and inequalities.
Real-World Examples

We use inequalities in many real-life situations. Here are some examples:
Amusement Parks
"You must be at least 48 inches tall to ride this roller coaster."
This can be written as: height ≥ 48 inches
Movie Ratings
"This movie is rated PG-13. You must be 13 or older to watch without a parent."
This can be written as: age ≥ 13
Speed Limits
"The speed limit on this road is 55 mph."
This means: speed ≤ 55 mph
Shopping
"You have $20 to spend. The toy costs $15. Do you have enough money?"
This can be written as: 15 ≤ 20 (Yes, you have enough!)
Real-World Connection
Inequalities help us set limits and make comparisons in everyday life, from age restrictions to speed limits to budget constraints.
Inequality Practice Quiz
Test your inequality knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about inequalities:
Math Trivia
Discover interesting facts about inequalities and math:
Historical Symbols
The inequality symbols > and < were introduced by British mathematician Thomas Harriot in his work "Artis Analyticae Praxis" published in 1631, over 10 years after his death.
Inequalities in Science
Inequalities are used in many scientific fields. Einstein's theory of relativity includes inequalities that describe how nothing can travel faster than the speed of light.
Computer Programming
Inequality symbols are essential in computer programming for making comparisons and decisions. Programs use inequalities to determine if conditions are met before executing certain code.
Famous Inequality
The Cauchy-Schwarz inequality is one of the most famous inequalities in mathematics. It's used in many areas including algebra, analysis, and probability theory.





