Isosceles Obtuse Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about this special type of triangle with easy explanations, properties, and practice activities
What is an Isosceles Obtuse Triangle?
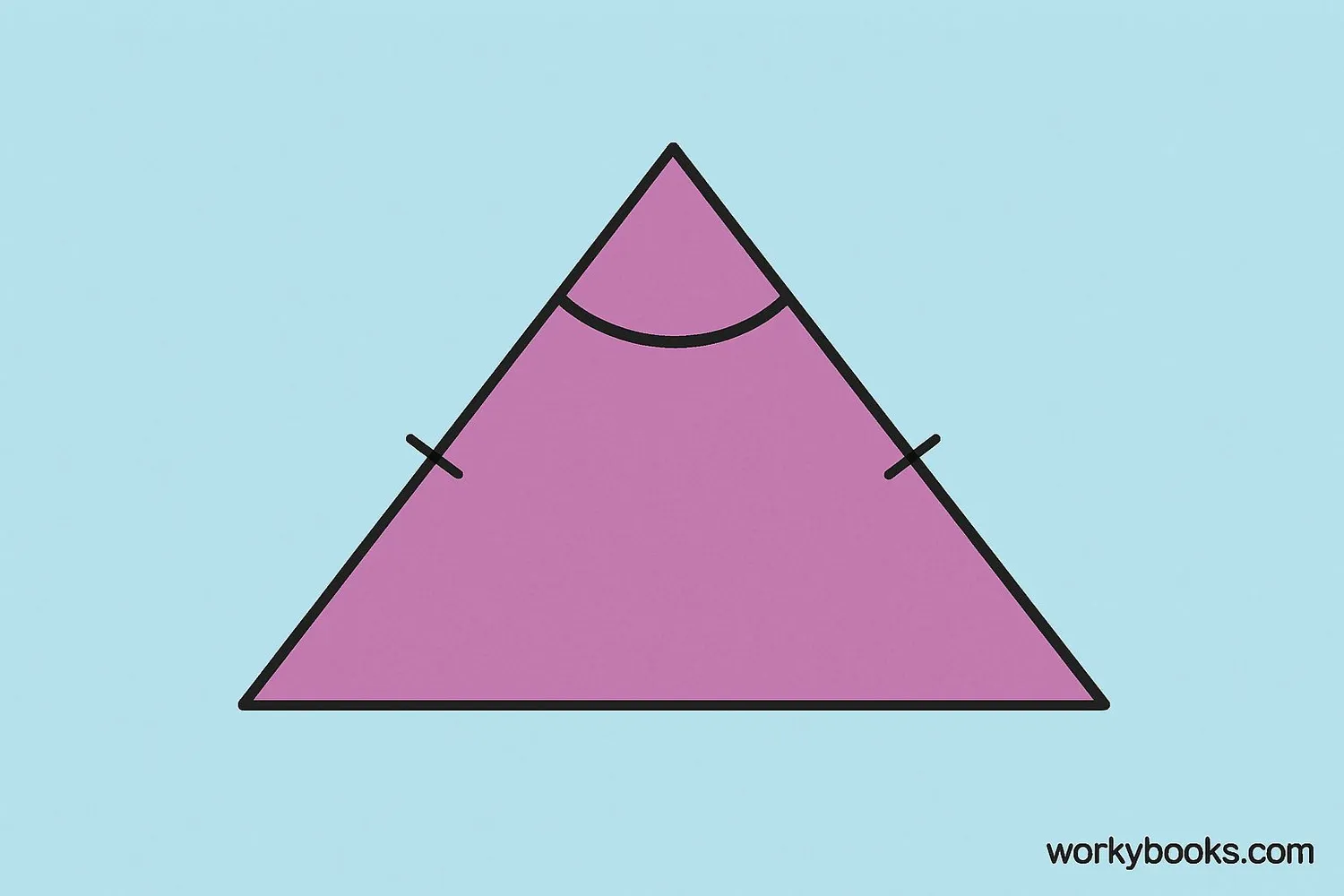
An isosceles obtuse triangle is a special type of triangle that has two important features:
1. Isosceles: This means it has two sides that are equal in length. We often mark these equal sides with small tick marks to show they're the same.
2. Obtuse: This means it has one angle that is greater than 90 degrees. An obtuse angle is wider than a right angle (which is exactly 90 degrees).
When we combine these two features, we get an isosceles obtuse triangle - a triangle with two equal sides and one angle that is greater than 90 degrees.
Key Concept
An isosceles obtuse triangle has two equal sides and one angle greater than 90 degrees. The two base angles (opposite the equal sides) are always acute (less than 90 degrees).
Properties of Isosceles Obtuse Triangles
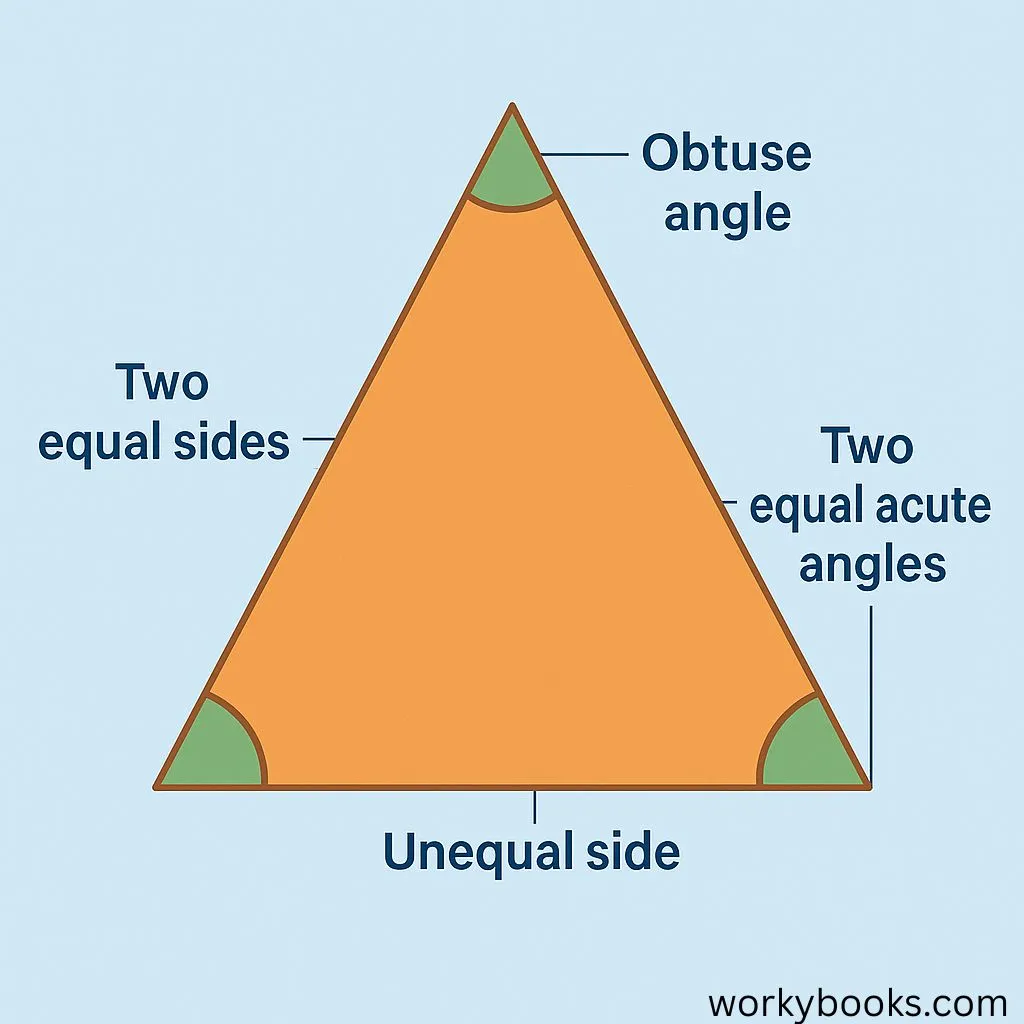
Isosceles obtuse triangles have special properties that make them unique:
- Two equal sides: The sides opposite the equal angles are always the same length.
- One obtuse angle: This angle is greater than 90 degrees but less than 180 degrees.
- Two acute angles: The other two angles are both acute (less than 90 degrees) and equal to each other.
- Angle sum: Like all triangles, the three angles always add up to 180 degrees.
- Unequal side: The side opposite the obtuse angle is the longest side of the triangle.
Angle Calculation
Since the two base angles are equal, we can calculate one if we know the other.
Remember
In an isosceles obtuse triangle, the obtuse angle is always between the two equal sides, and the base angles (at the unequal side) are always equal and acute.
Real-World Examples
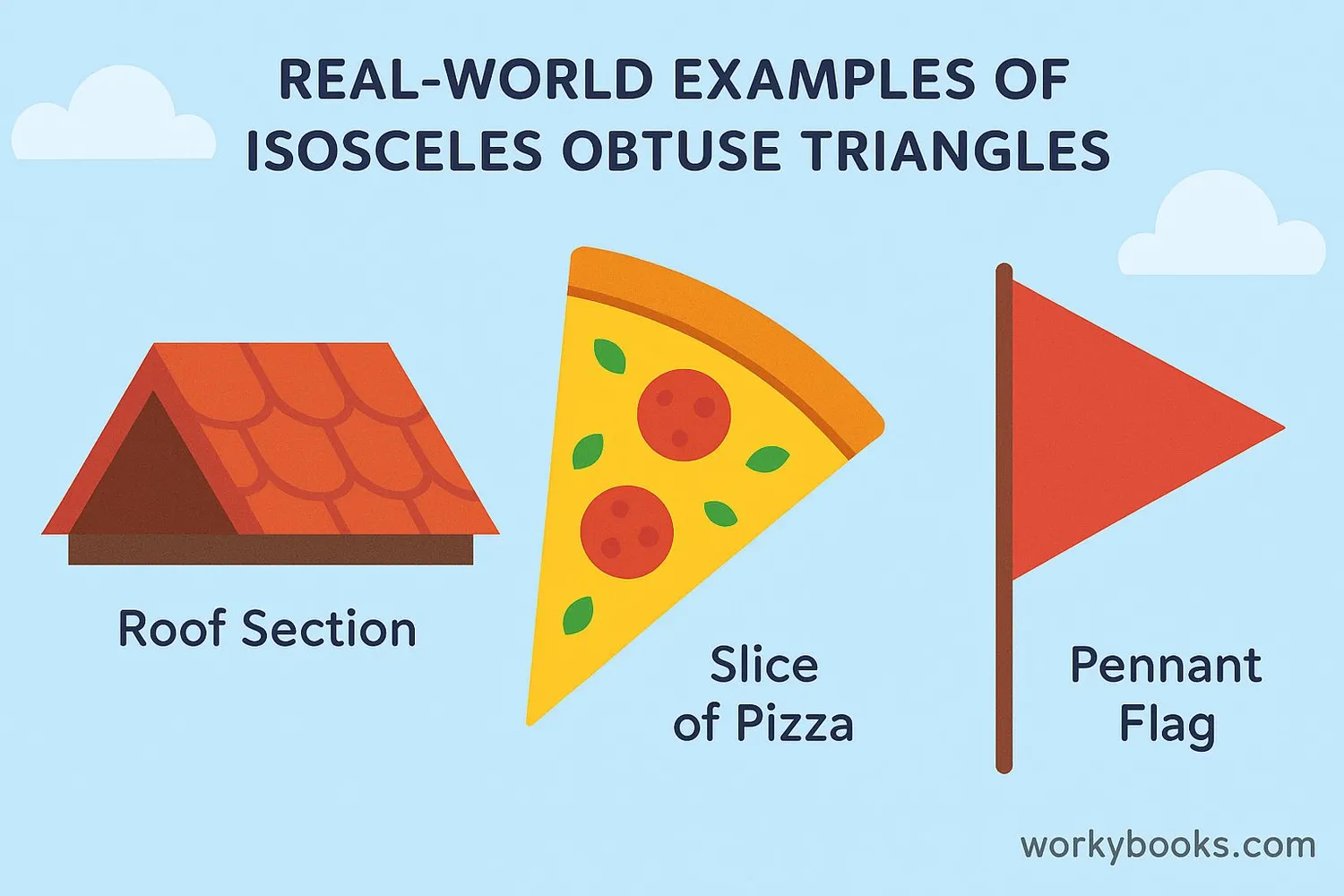
Isosceles obtuse triangles appear in many places in our daily lives. Here are some examples:
Example 1: Roof sections often form isosceles obtuse triangles. The two equal sides are the roof slopes, and the obtuse angle is at the peak.
Example 2: Some pennant flags or decorative banners have this shape, with two equal sides and a wide angle at the top.
Example 3: Certain types of sandwiches or pizza slices can be cut into isosceles obtuse triangles.
Example 4: In architecture, isosceles obtuse triangles are sometimes used in truss designs for bridges and roofs because of their stability.
Look around you - you might spot isosceles obtuse triangles in buildings, art, or even in nature!
Math Connection
If an isosceles obtuse triangle has an obtuse angle of 120 degrees, what are the measurements of the other two angles? (Remember: all angles add to 180 degrees, and the base angles are equal!)
Triangle Practice Quiz
Test your knowledge about isosceles obtuse triangles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about isosceles obtuse triangles:
Triangle Trivia
Discover interesting facts about triangles and geometry:
Ancient Geometry
The study of triangles dates back to ancient Egypt and Babylon, where they were used for surveying land and building pyramids. The Greek mathematician Euclid wrote extensively about triangles in his famous work "Elements" around 300 BCE.
Strong Shapes
Triangles are the strongest geometric shape because they distribute weight evenly. This is why you see triangles in bridges, roof trusses, and other structures that need to be strong and stable.
Space Triangles
NASA engineers use triangular shapes in many spacecraft designs because of their strength and stability. The Apollo lunar module had a triangular window design for maximum visibility and structural integrity.
Triangle in Art
Many famous artists, including Leonardo da Vinci and Piet Mondrian, used triangles extensively in their compositions. The triangular format helps create balance and direct the viewer's eye through the artwork.





