Isosceles Trapezoid - Definition, Examples, Quiz, FAQ, Trivia
Learn about this special quadrilateral with equal legs and symmetrical properties
What is an Isosceles Trapezoid?
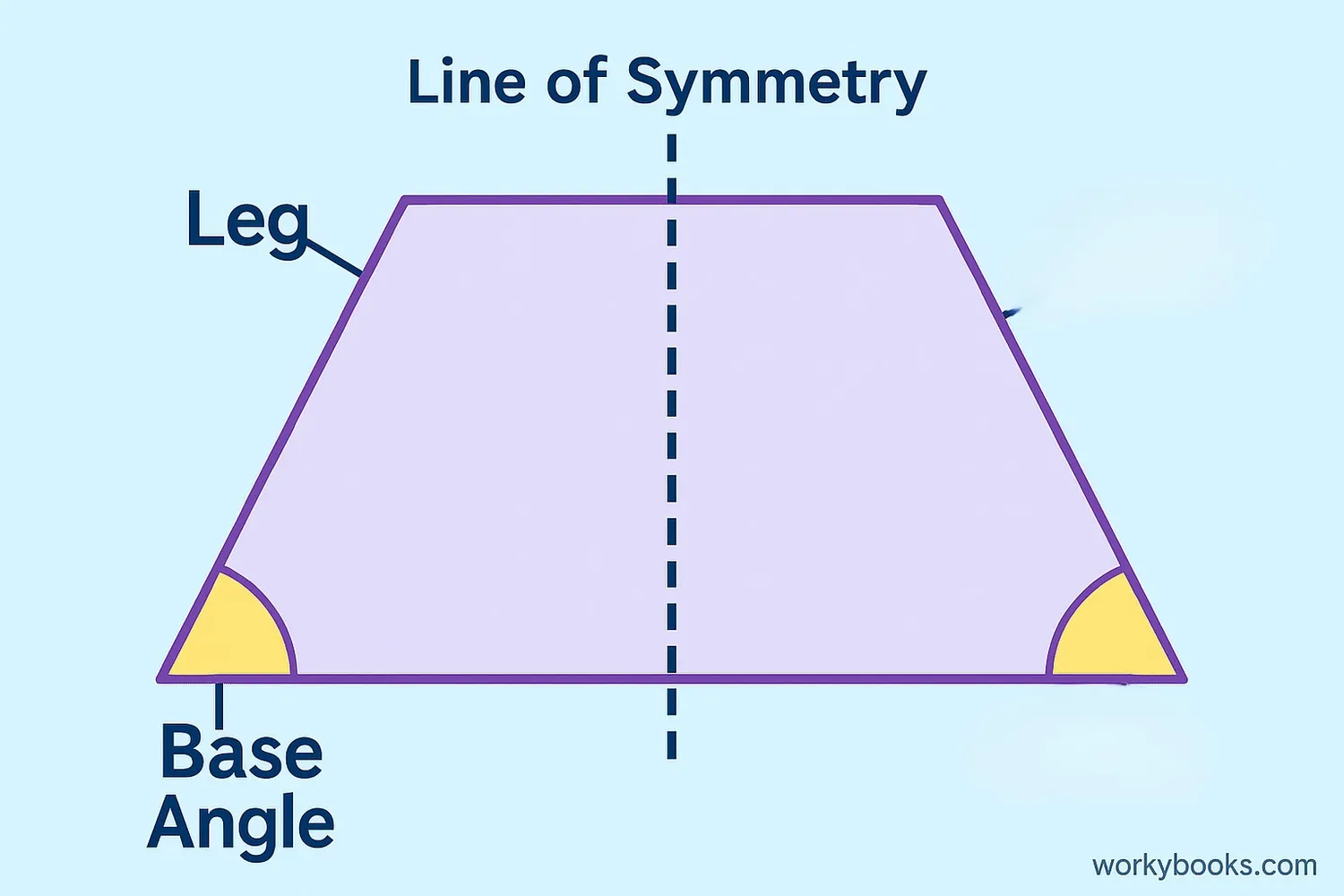
An isosceles trapezoid is a special type of trapezoid where the two legs (non-parallel sides) are equal in length. Just like an isosceles triangle has two equal sides, an isosceles trapezoid has two equal legs.
In a regular trapezoid, only one pair of sides is parallel (the bases). But in an isosceles trapezoid, not only are the bases parallel, but the legs are also equal in length. This gives the shape symmetry that regular trapezoids don't have.
Isosceles trapezoids are all around us! You might see them in architecture, bridges, or even in the shapes of certain objects like handbags or decorative items.
Key Concept
An isosceles trapezoid has exactly one pair of parallel sides (the bases) and the legs are equal in length.
Properties of Isosceles Trapezoids
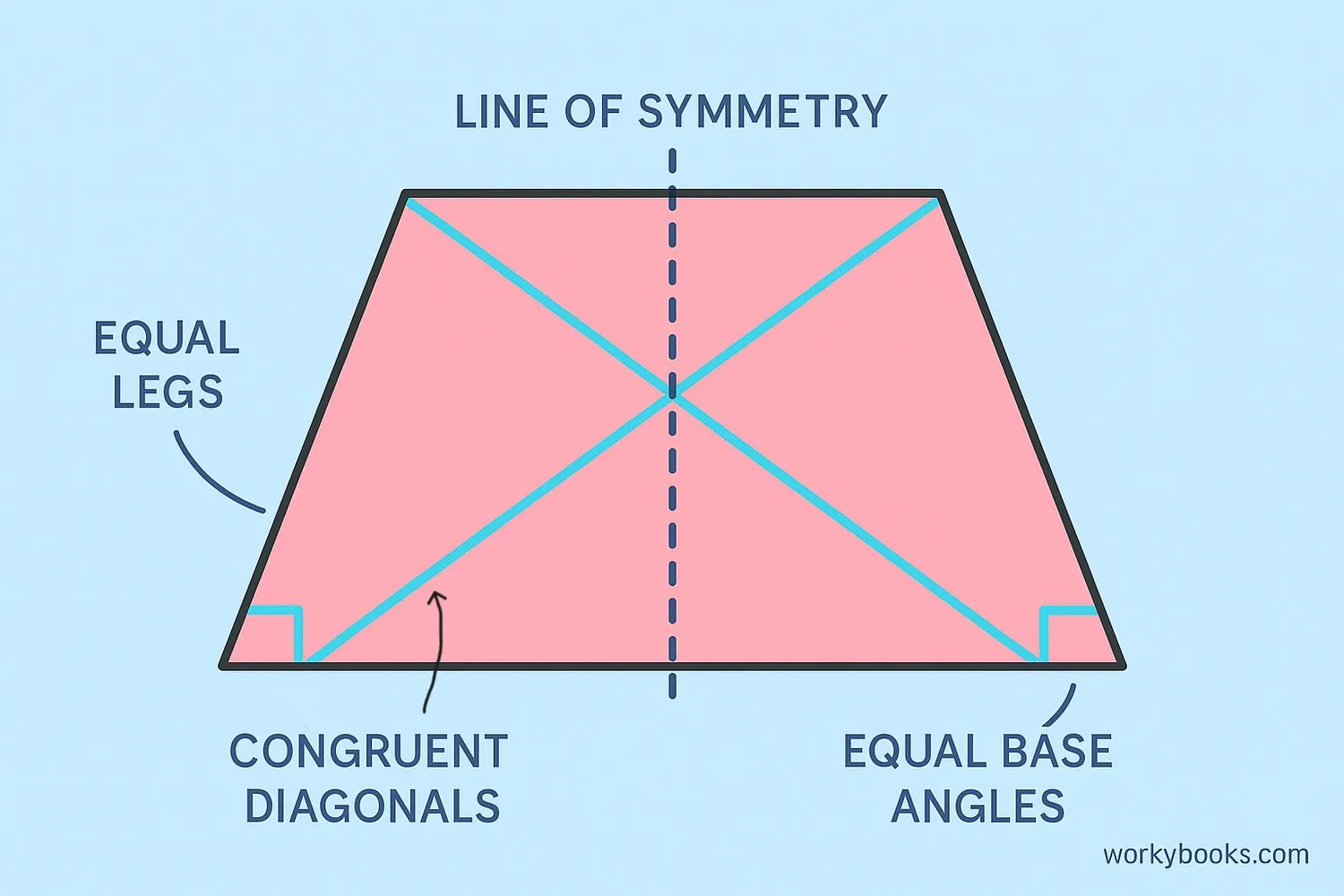
Isosceles trapezoids have several special properties that make them different from regular trapezoids:
- Equal legs: The two non-parallel sides (legs) are equal in length.
- Equal base angles: The angles adjacent to each base are equal. This means the lower base angles are equal, and the upper base angles are equal.
- Congruent diagonals: The diagonals (lines connecting opposite vertices) are equal in length.
- Symmetry: Isosceles trapezoids have one line of symmetry that goes through the midpoints of both bases.
- Supplementary angles: Angles adjacent to the same leg add up to 180 degrees.
Remember
All isosceles trapezoids are trapezoids, but not all trapezoids are isosceles trapezoids. The isosceles ones have those special equal legs!
Area of an Isosceles Trapezoid
To find the area of an isosceles trapezoid, we use the same formula as for any trapezoid:
Area Formula
Where:
A = area
h = height (distance between bases)
a = length of first base
b = length of second base
Example: Find the area of an isosceles trapezoid with bases of 8 cm and 12 cm, and a height of 5 cm.
Step 1: Add the bases → 8 + 12 = 20 cm
Step 2: Divide by 2 → 20 ÷ 2 = 10 cm
Step 3: Multiply by height → 10 × 5 = 50 cm²
So the area is 50 square centimeters.
Remember
The height must be perpendicular to the bases. The slanted legs don't determine the height!
Angles in Isosceles Trapezoids
Isosceles trapezoids have special angle properties that help us identify them and solve geometry problems:
Base angles: The angles adjacent to each base are equal. This means:
- The two angles along the longer base are equal
- The two angles along the shorter base are equal
Supplementary angles: Angles along the same leg add up to 180 degrees. For example, if one angle measures 60 degrees, the angle next to it on the same leg will measure 120 degrees.
Example: If an isosceles trapezoid has base angles of 60 degrees on the longer base, then the angles on the shorter base will be 120 degrees (because 180 - 60 = 120).
Angle Tip
If you know one angle in an isosceles trapezoid, you can find all the other angles using these special properties!
Real-World Examples

Isosceles trapezoids appear in many places in our daily lives. Here are some examples:
Bridges: Many bridge supports use isosceles trapezoid shapes because they're strong and stable.
Architecture: Windows, doors, and decorative elements sometimes have isosceles trapezoid shapes.
Everyday objects: Handbags, bowls, and containers often have isosceles trapezoid shapes when viewed from the side.
Mathematics: Isosceles trapezoids are used in geometry problems and in creating tessellations (patterns that cover a surface without gaps).
Look around you - can you spot any isosceles trapezoids in your environment?
Example Problem
An isosceles trapezoid has bases of 10 cm and 16 cm, and legs of 5 cm each. The height is 4 cm. What is its area?
Solution: Area = height × (base1 + base2)/2 = 4 × (10 + 16)/2 = 4 × 26/2 = 4 × 13 = 52 cm²
Isosceles Trapezoid Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about isosceles trapezoids:
Geometry Trivia
Discover interesting facts about geometry and trapezoids:
Ancient Geometry
The study of trapezoids dates back to ancient Greek mathematicians. The word "trapezoid" comes from the Greek word "trapeza" meaning table, and "eidos" meaning shape or form.
Architectural Strength
Isosceles trapezoids are often used in architecture and bridge design because their shape provides excellent stability and weight distribution, making structures stronger.
Special Cases
Parallelograms, rectangles, and squares are all special types of trapezoids according to some mathematical definitions, though not all mathematicians agree on this classification.
Nature's Patterns
While perfect isosceles trapezoids are rare in nature, many natural formations like certain crystal structures and rock formations approximate this shape due to erosion patterns.





