Isosceles Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about isosceles triangles with easy explanations, properties, and examples
What is an Isosceles Triangle?
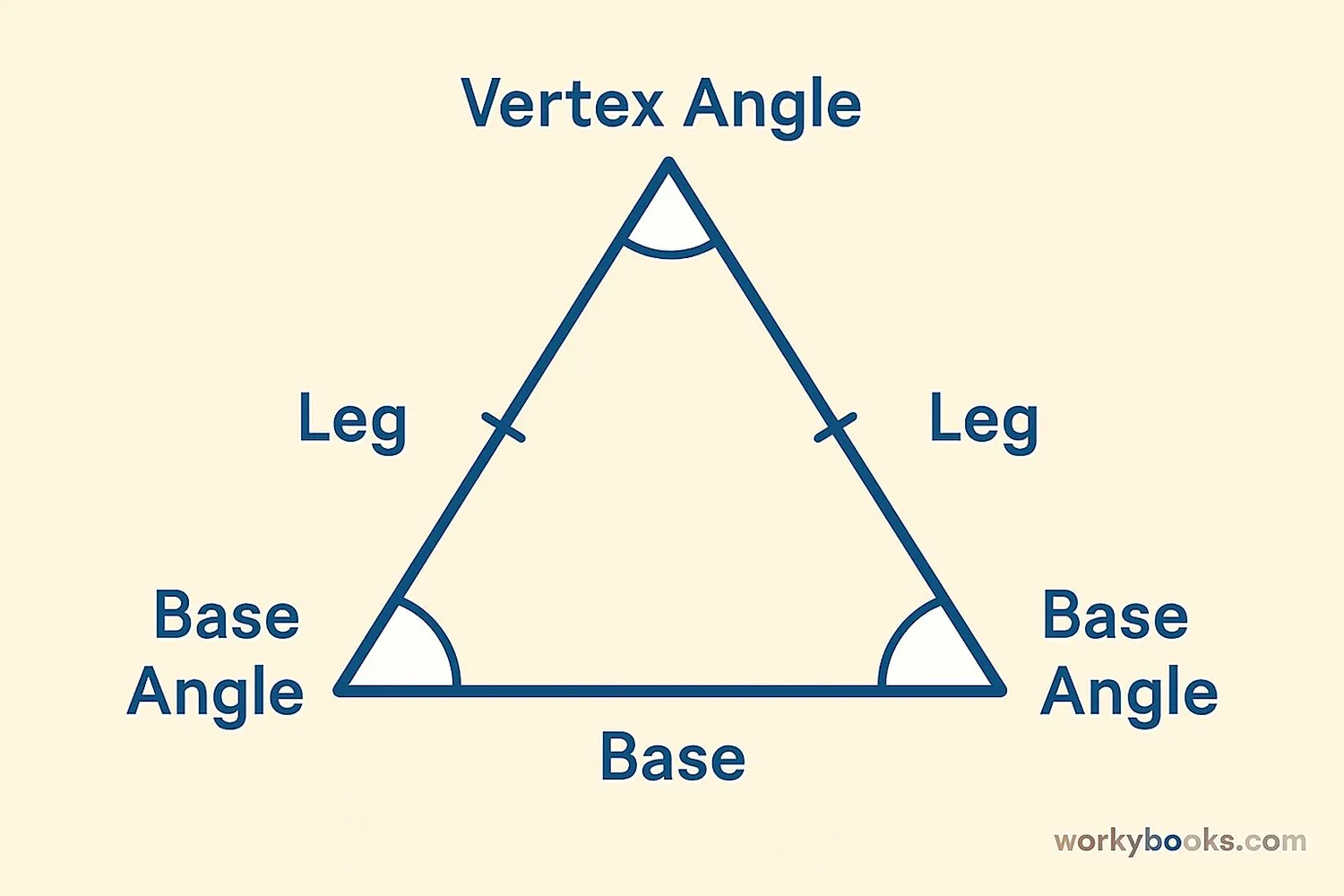
An isosceles triangle is a special type of triangle that has at least two sides of equal length. These equal sides are called the "legs" of the triangle, and the third side is called the "base".
Because of these equal sides, the angles opposite them are also equal. These are called the "base angles". The angle between the two legs is called the "vertex angle".
Imagine a triangle that looks like a slice of pizza or the roof of a house - these are everyday examples of isosceles triangles!
Key Concept
In an isosceles triangle, two sides are equal (legs), and two angles are equal (base angles).
Properties of Isosceles Triangles
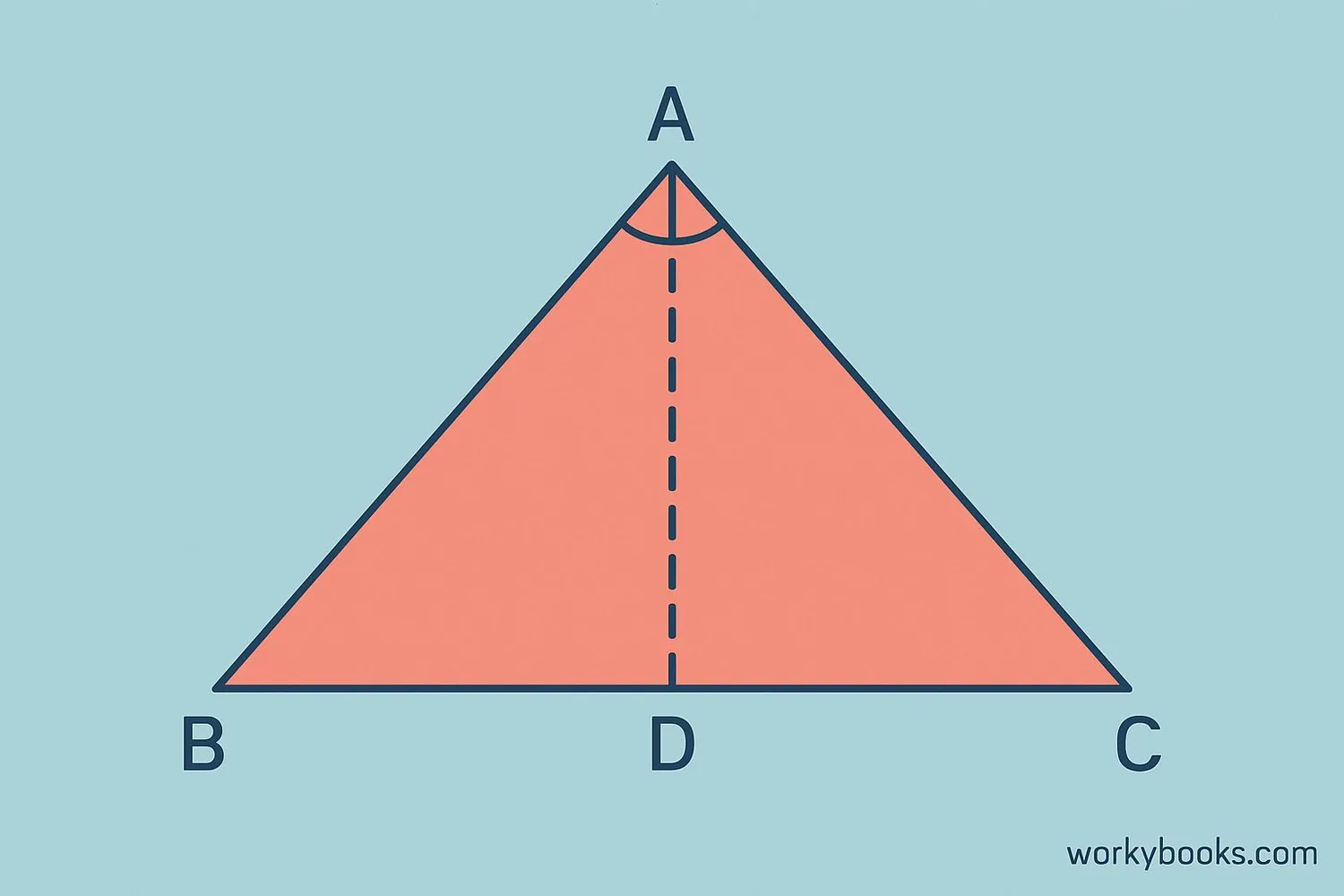
Isosceles triangles have some special properties that make them unique:
1. Two equal sides (legs) - The sides connected to the vertex are equal
2. Two equal angles (base angles) - The angles opposite the equal sides are equal
3. Symmetry - An altitude drawn from the vertex angle to the base:
- Bisects the base (divides it into two equal parts)
- Bisects the vertex angle (divides it into two equal angles)
- Is also the median and the angle bisector
These properties make isosceles triangles very useful in architecture, engineering, and design!
Remember
In any triangle, the sum of all angles is always 180°. In an isosceles triangle, if you know the vertex angle, you can find the base angles, and vice versa.
Types of Isosceles Triangles
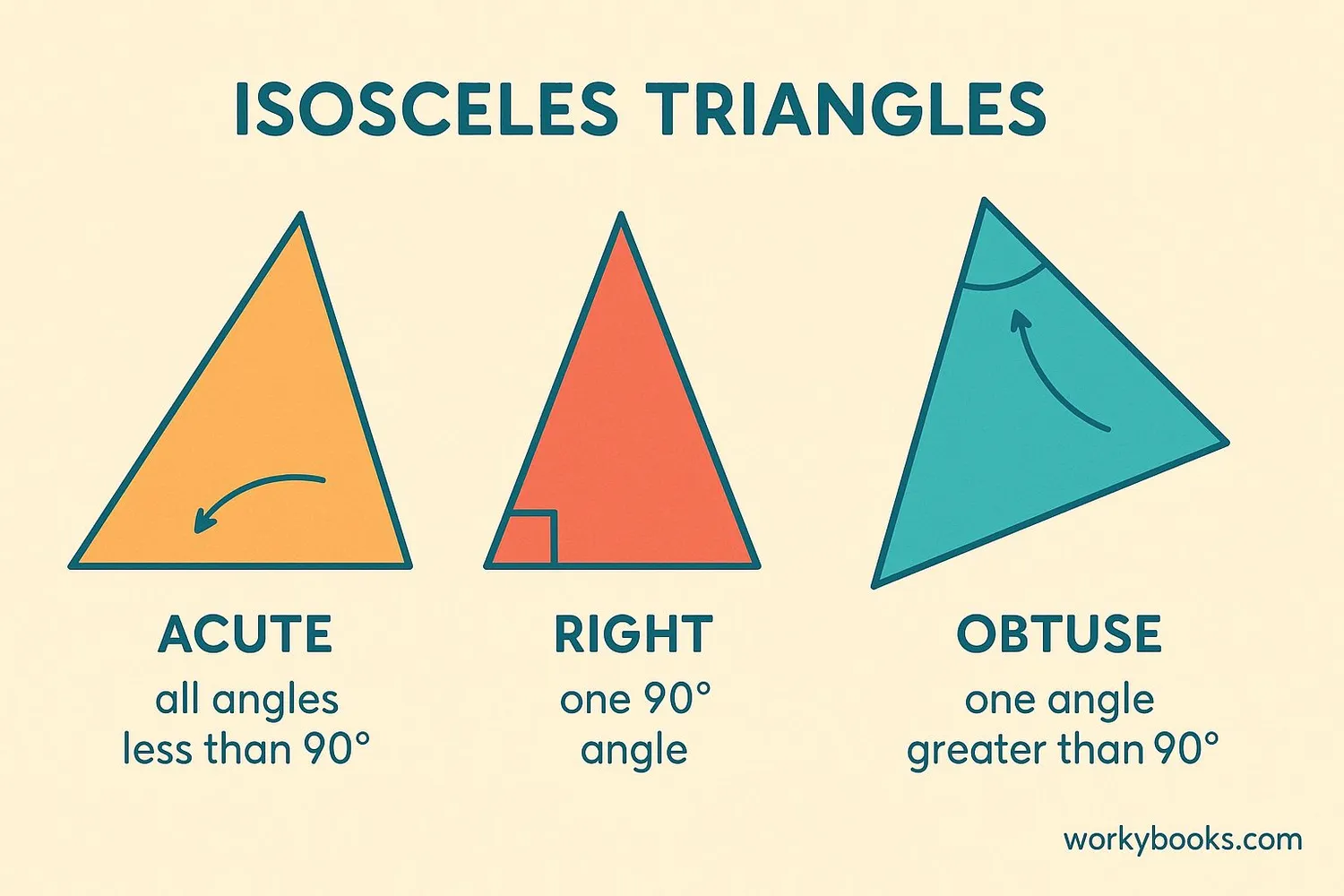
Isosceles triangles can be classified based on their angles. There are three main types:
Acute Isosceles
All angles less than 90°
Right Isosceles
One right angle (90°)
Obtuse Isosceles
One angle greater than 90°
Right isosceles triangle is a special case where the two legs are equal and form a right angle. The base angles in this case are both 45°.
Fun fact: The right isosceles triangle is the only triangle that has two equal sides and contains a right angle!
Formulas for Isosceles Triangles
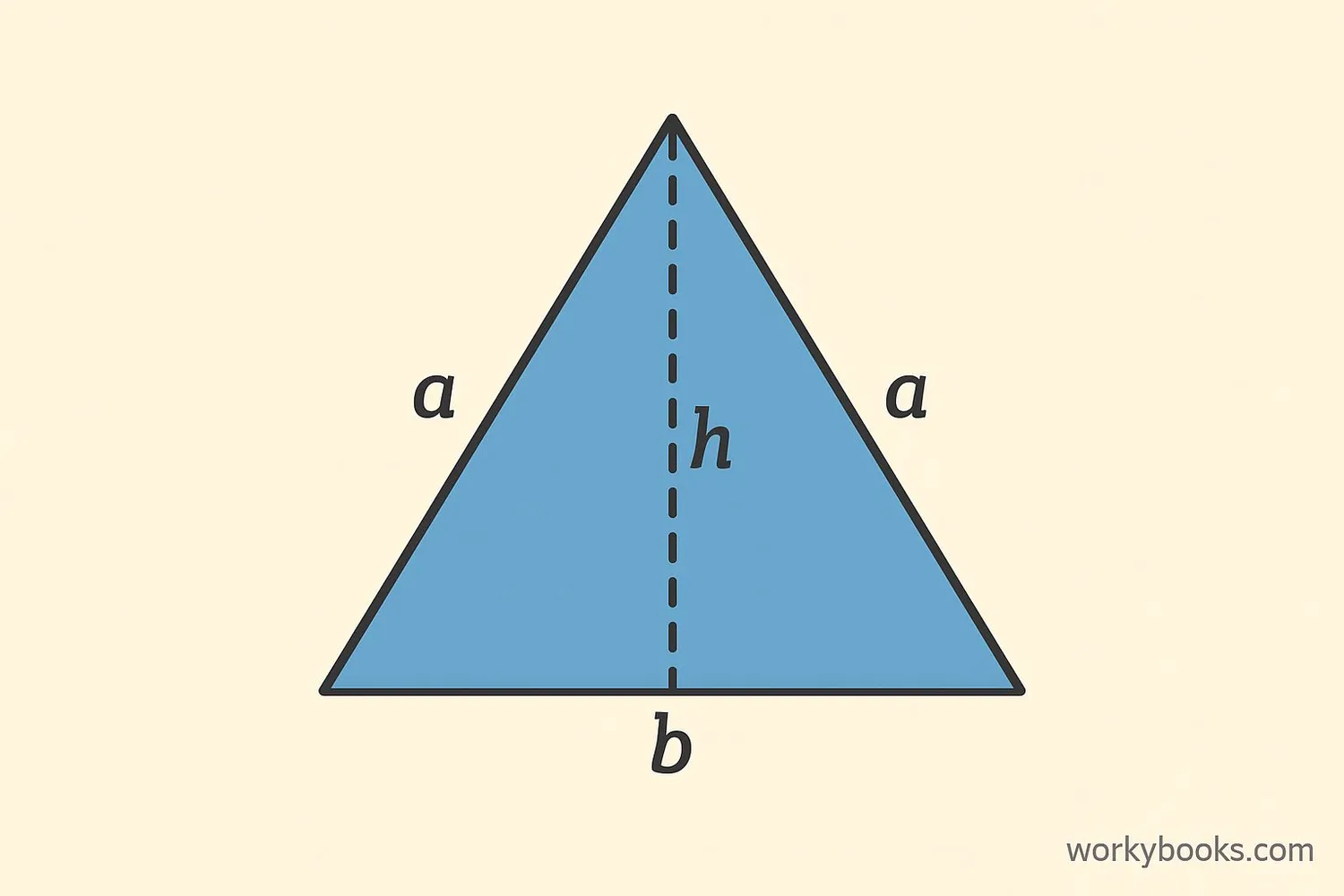
We can calculate the perimeter and area of an isosceles triangle using these formulas:
Perimeter Formula
Where 'a' is the length of the two equal sides, and 'b' is the base length.
Area Formula
Where 'b' is the base length and 'h' is the height to that base.
Example: Calculating Perimeter
An isosceles triangle has legs of 8 cm and a base of 5 cm. What is its perimeter?
Solution: P = 2a + b = 2(8) + 5 = 16 + 5 = 21 cm
Example: Calculating Area
An isosceles triangle has a base of 10 cm and a height of 12 cm. What is its area?
Solution: A = (b × h) ÷ 2 = (10 × 12) ÷ 2 = 120 ÷ 2 = 60 cm²
Real-World Examples
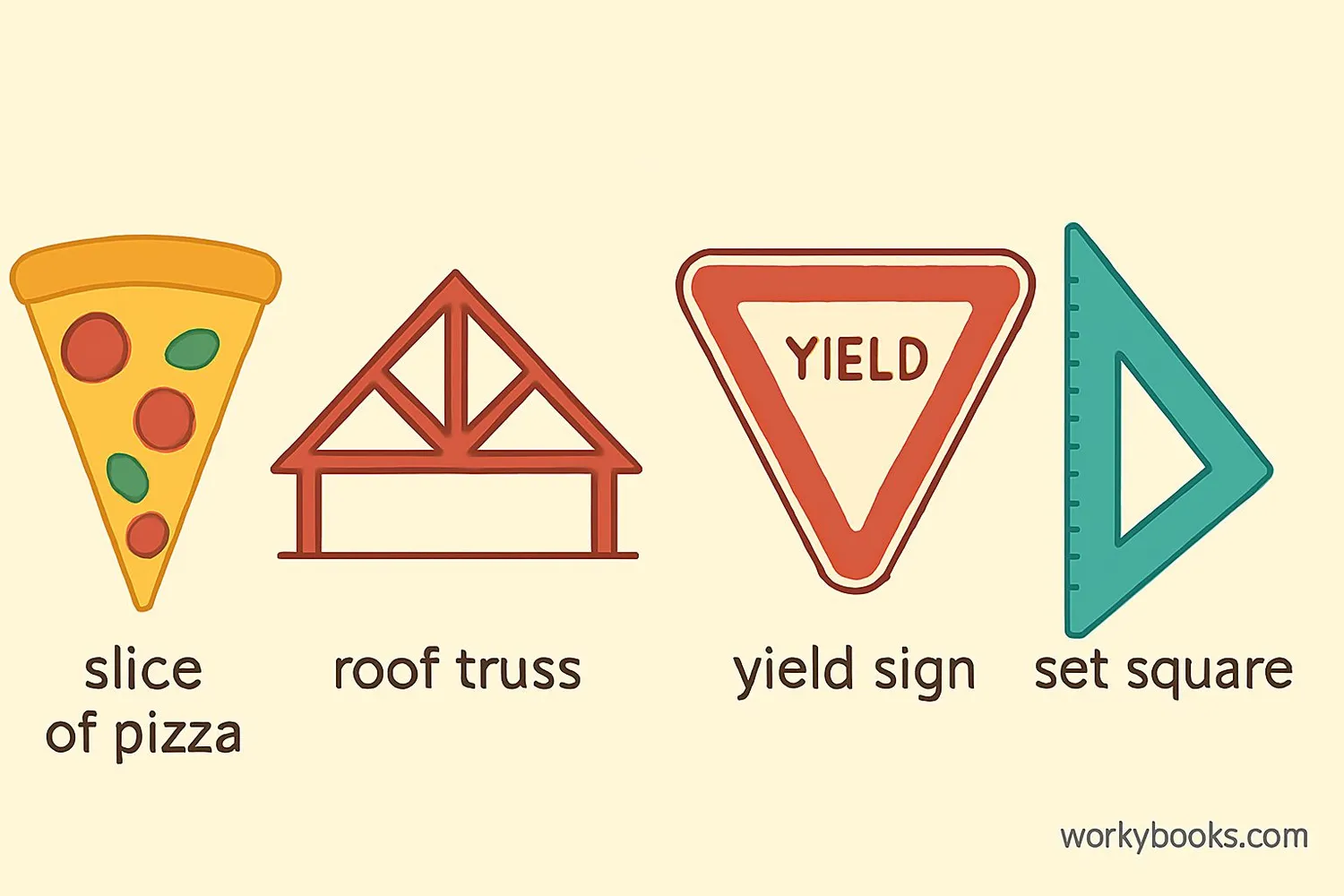
Isosceles triangles are all around us! Here are some real-world examples:
1. Roof trusses: Many house roofs have isosceles triangle shapes for strength and stability.
2. Pizza slices: A slice of pizza is usually an isosceles triangle with two equal sides.
3. Yield signs: The familiar upside-down triangle is an isosceles triangle.
4. Set squares: Some drawing tools are right-angled isosceles triangles.
5. Bridges: Many bridge supports use isosceles triangles to distribute weight evenly.
Next time you look around, see how many isosceles triangles you can spot!
Remember
The isosceles triangle is one of the strongest shapes in construction because it distributes weight evenly to its base.
Isosceles Triangle Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about isosceles triangles:
Triangle Trivia
Discover interesting facts about triangles:
Ancient Geometry
The properties of isosceles triangles were studied as far back as 300 BC by Greek mathematicians like Euclid. They appear in Euclid's famous work "Elements".
Strong Shapes
Isosceles triangles are one of the strongest geometric shapes. Engineers use them in bridges and towers because they distribute weight efficiently and resist bending.
Nature's Triangles
Isosceles triangles appear throughout nature - in the branching patterns of trees, the formation of crystals, and even in the structure of DNA molecules.
Tallest Structure
The Eiffel Tower in Paris uses many isosceles triangles in its design. This triangular framework makes it both lightweight and extremely strong.





