Law of Cosines - Definition, Examples, Quiz, FAQ, Trivia
Learn how to solve triangles using the cosine formula with visual examples and interactive practice
What is the Law of Cosines?
The Law of Cosines is a special math formula that helps us solve triangles when we know some sides and angles. Think of it as a superpower for triangles!
When you have a triangle that isn't a right triangle (where one angle is exactly 90 degrees), the Law of Cosines helps you find missing sides or angles.
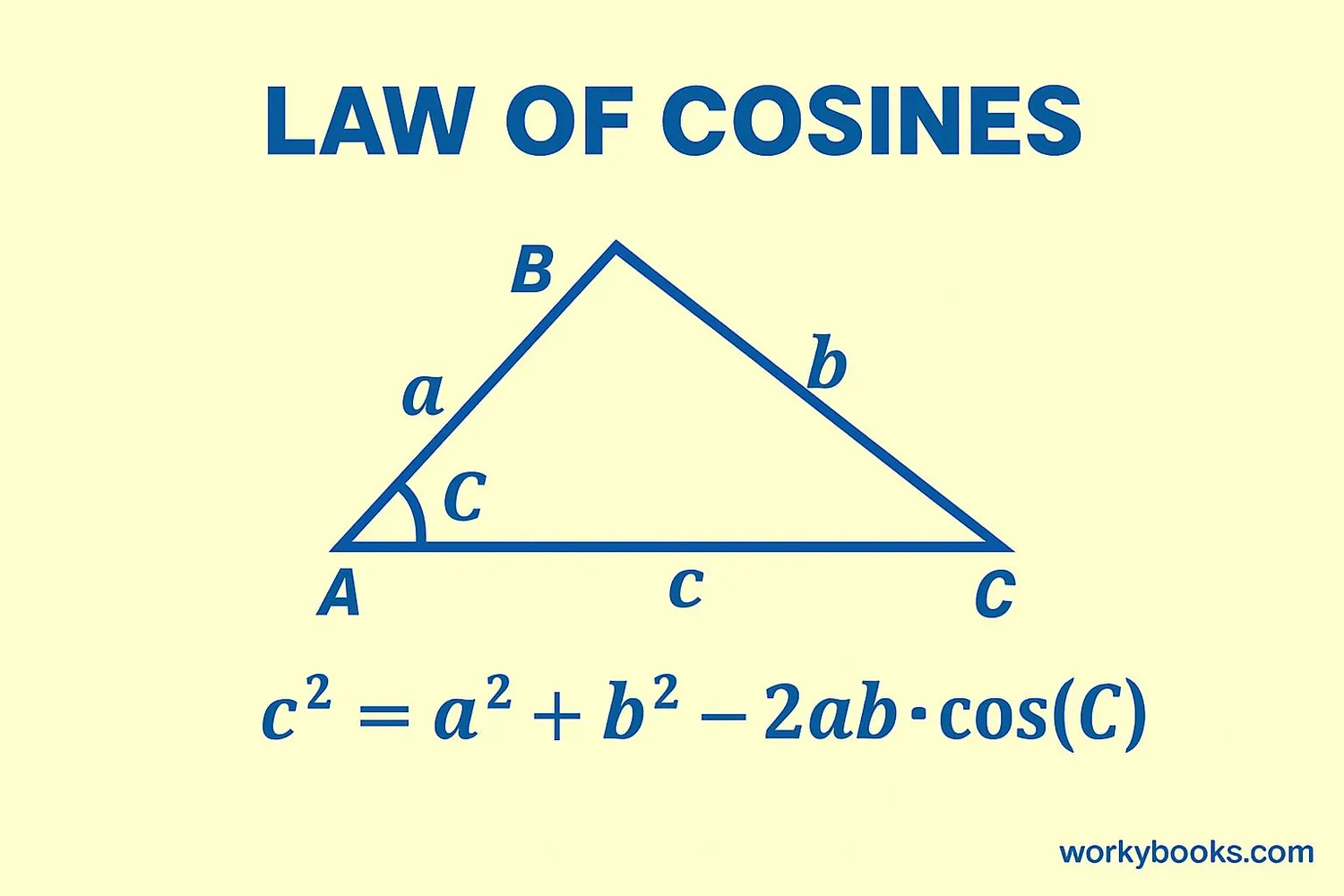
The formula looks like this:
Law of Cosines Formula
Where c is the side opposite angle C, and a and b are the other two sides.
Key Concept
The Law of Cosines works for any triangle, not just right triangles. It's especially useful when you know two sides and the angle between them.
How to Use the Law of Cosines
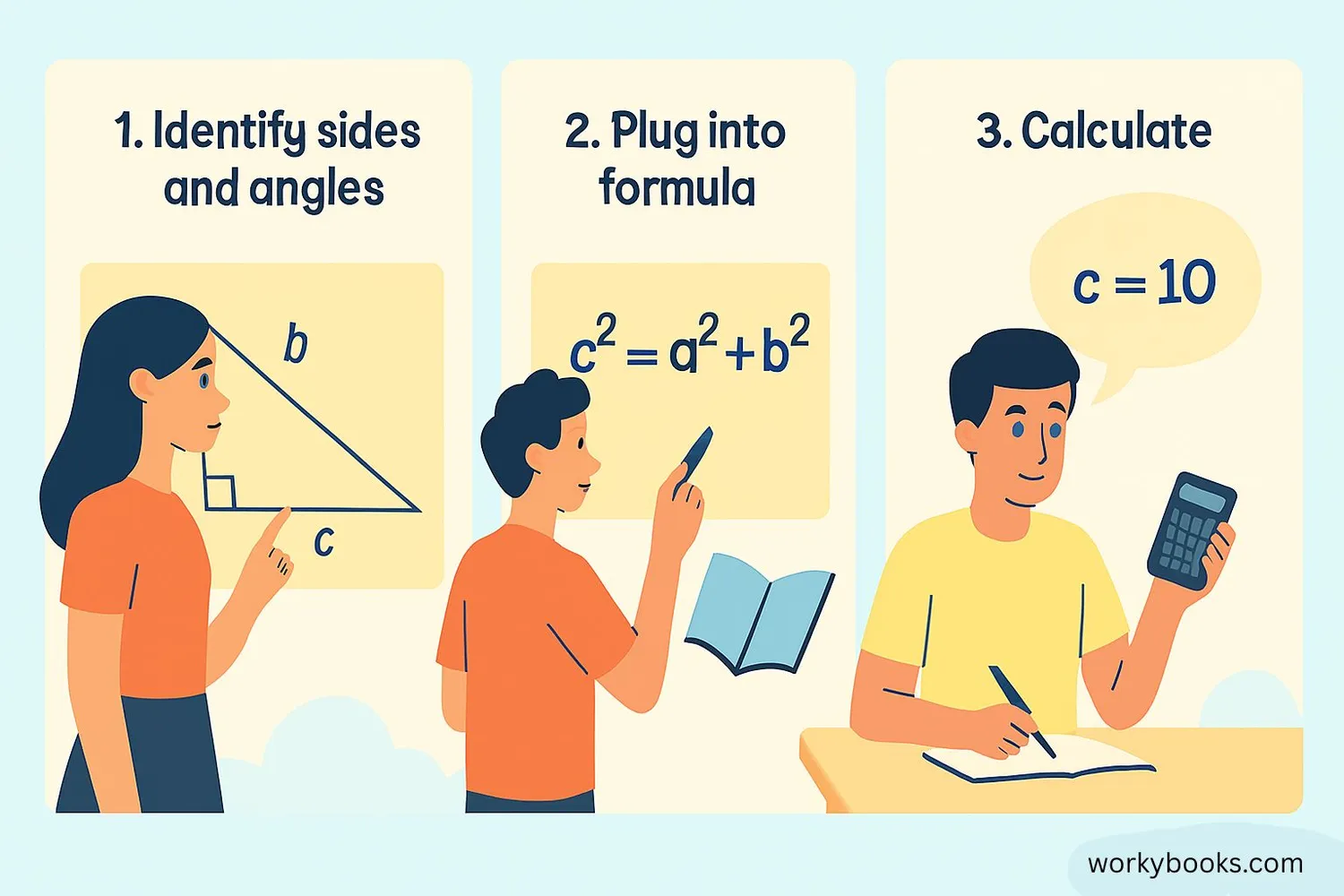
Using the Law of Cosines is like following a recipe. Here are the steps:
Step 1: Identify which sides and angles you know. Draw a sketch if it helps!
Step 2: Choose the right version of the formula. If you're looking for side c, use:
Step 3: Plug in the values you know. Make sure your calculator is in degree mode if angles are in degrees.
Step 4: Solve the equation. If you're finding a side, you'll need to take the square root at the end.
Step 5: Check if your answer makes sense. The longest side should be opposite the largest angle.
Remember
When you know two sides and the angle between them, the Law of Cosines helps you find the third side.
Examples and Practice
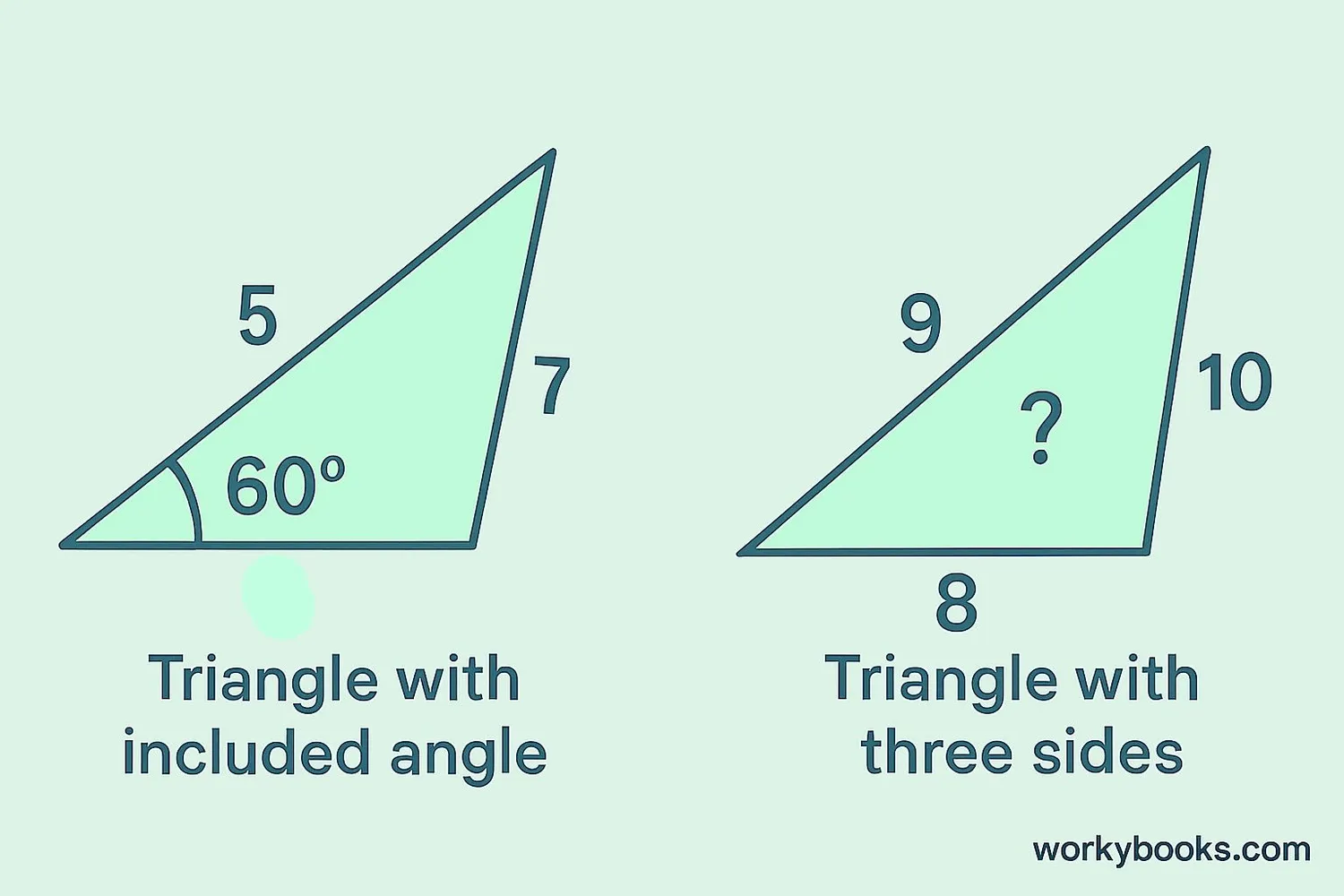
Let's practice with some examples:
Example 1: Find side c when a = 5, b = 7, and angle C = 60°
Solution: c² = 5² + 7² - 2·5·7·cos(60°)
c² = 25 + 49 - 70·0.5
c² = 74 - 35 = 39
c = √39 ≈ 6.24
Example 2: Find angle C when sides a = 8, b = 9, c = 10
Solution: Rearrange the formula: cos(C) = (a² + b² - c²)/(2ab)
cos(C) = (64 + 81 - 100)/(2·8·9) = (45)/(144) = 0.3125
C = cos⁻¹(0.3125) ≈ 71.8°
Practice Tip
Always draw a sketch of the triangle and label what you know. This helps you choose the right formula!
Real-World Applications

The Law of Cosines isn't just for math class! Here's where you might see it in the real world:
Navigation: Pilots and sailors use it to calculate distances between two points when they know distances from a third point.
Construction: Builders use it to calculate roof slopes and diagonal supports.
Surveying: Land surveyors use it to measure distances between landmarks when they can't measure directly.
Physics: Scientists use it to calculate forces acting at angles to each other.
Robotics: Engineers use it to program robotic arms to reach precise positions.
Fun Fact
The Law of Cosines was first described by Persian mathematician Jamshīd al-Kāshī in the 15th century!
Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the Law of Cosines:
Math Trivia
Discover interesting facts about triangles and trigonometry:
Ancient Origins
The principles behind the Law of Cosines were known to ancient Greek mathematicians over 2,000 years ago! Euclid's Elements contains theorems that are similar to the Law of Cosines.
GPS Technology
Your phone's GPS uses trigonometry like the Law of Cosines to calculate your position by measuring distances to multiple satellites. It's trigonometry in your pocket!
Space Exploration
NASA uses the Law of Cosines to calculate trajectories for spacecraft. When sending rockets to the Moon or Mars, engineers use trigonometry to plan the most efficient paths.
Triangle World Record
The largest triangle ever drawn was created in the desert of Nevada, USA. Each side was over 1 kilometer long! Surveyors used trigonometry to make sure the angles were precise.





