Law of Sines - Definition, Examples, Quiz, FAQ, Trivia
Learn to solve triangles using the Law of Sines with easy explanations and practice activities
What is the Law of Sines?
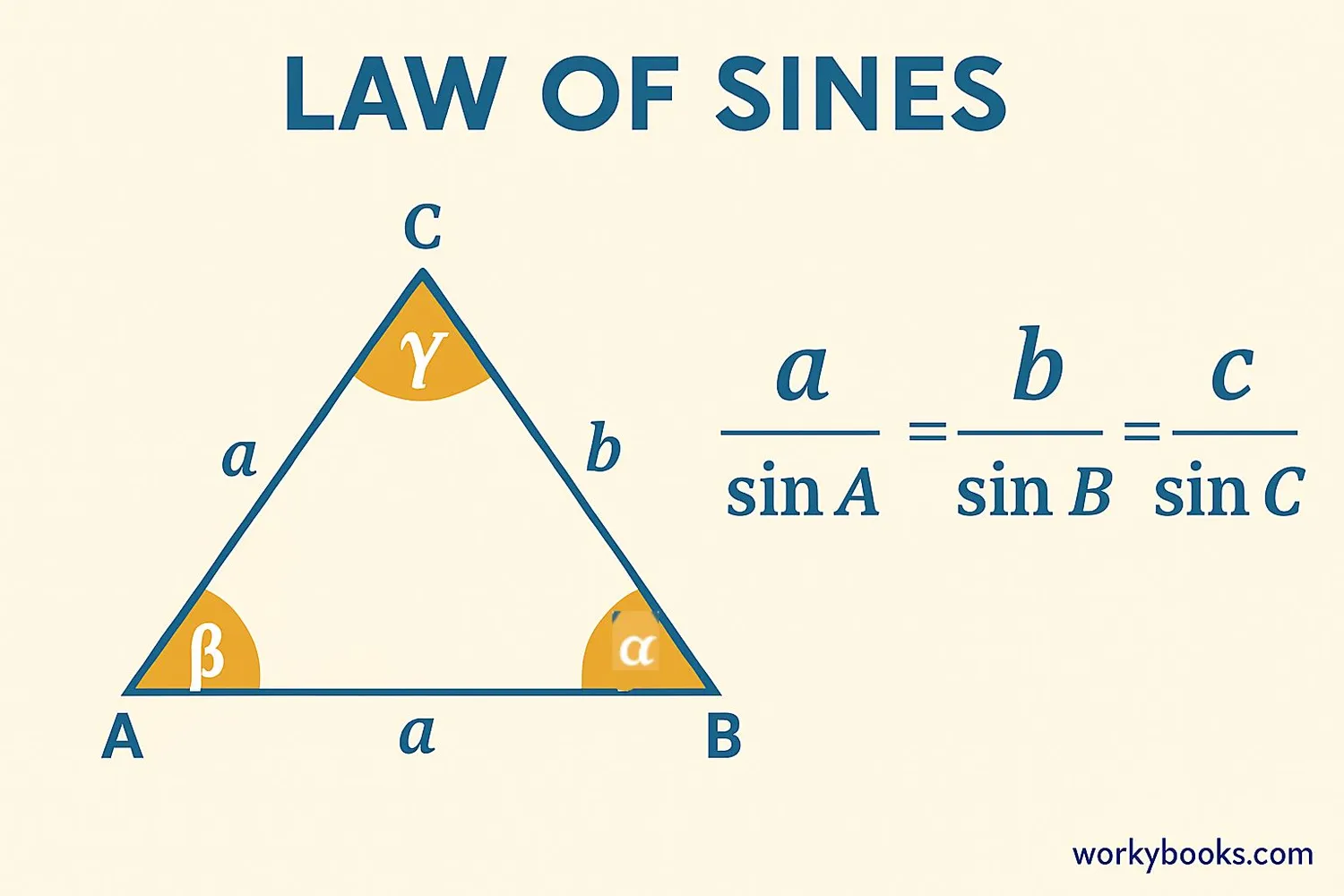
The Law of Sines (also called the Sine Rule) is a special math rule that helps us solve triangles when we know certain measurements. It connects the lengths of a triangle's sides with the sines of its opposite angles.
Here's the formula:
Law of Sines Formula
Where:
a, b, c = lengths of the triangle's sides
A, B, C = angles opposite those sides
Key Concept
The Law of Sines shows that the ratio of any side length to the sine of its opposite angle is equal for all three sides of a triangle.
How to Use the Law of Sines
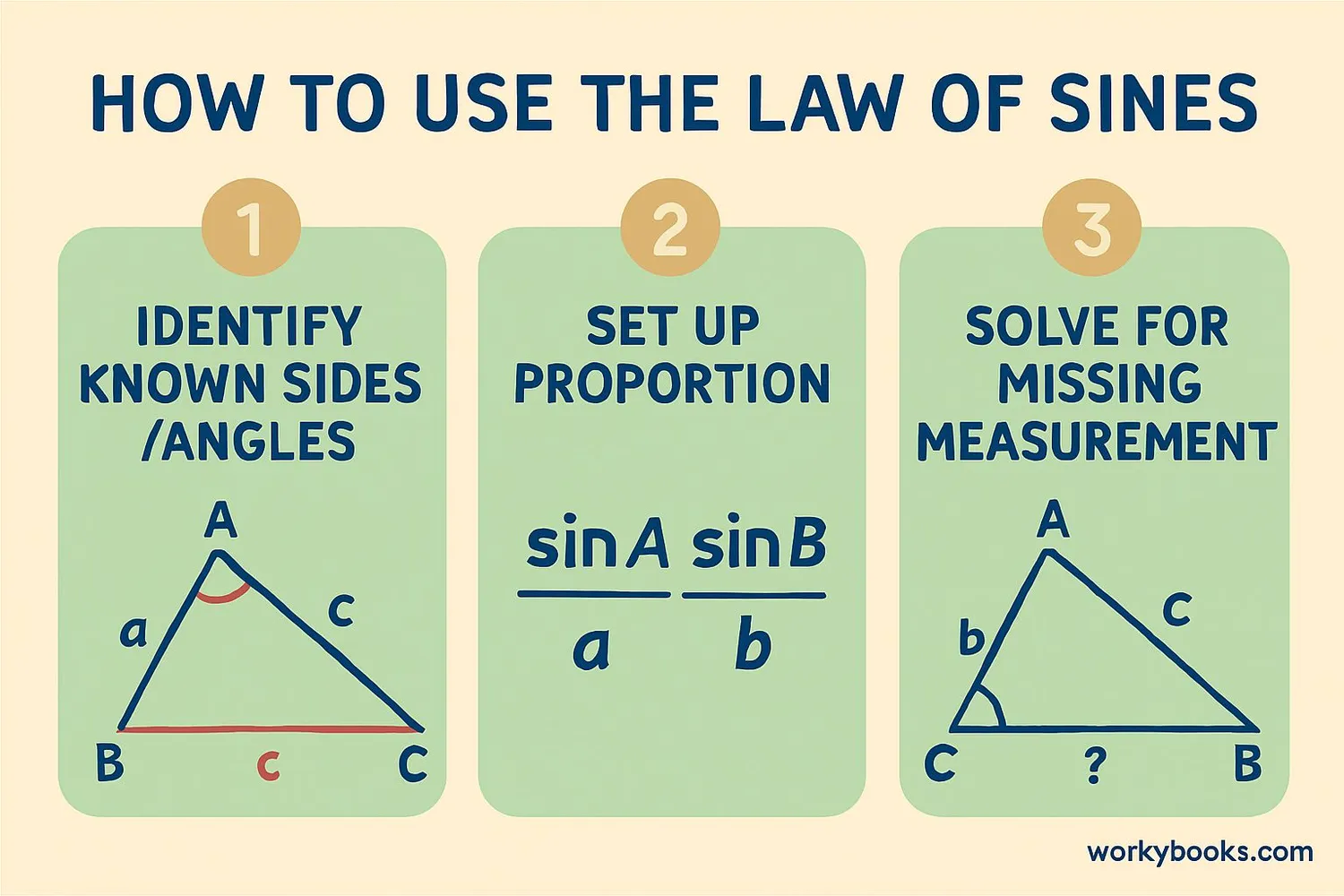
Let's learn how to use the Law of Sines with these simple steps:
Step 1: Identify what you know - two angles and one side (AAS or ASA) or two sides and an angle opposite one of them (SSA).
Step 2: Write the Law of Sines proportion that includes your known measurements and the measurement you want to find.
Step 3: Solve the equation for the missing measurement.
Example: If we know angle A = 30°, angle B = 45°, and side a = 8 cm, we can find side b:
a/sinA = b/sinB → 8/sin30° = b/sin45°
Solve for b: b = (8 × sin45°) / sin30° ≈ (8 × 0.7071) / 0.5 ≈ 11.31 cm
Remember to check if you might have the ambiguous case (when using SSA information), where there could be two possible solutions!
Remember
The Law of Sines works best when you know either: two angles and one side (AAS or ASA) or two sides and an angle opposite one of them (SSA).
Law of Sines Examples
Let's practice with some real-world examples:
Example 1 (AAS): A surveyor measures two angles of a triangular plot of land (65° and 40°) and the length of one side (100m). Find the other sides.
Solution: First find the third angle (180° - 65° - 40° = 75°). Then use Law of Sines to find the other sides.
Example 2 (SSA): Two lighthouses are 5 km apart. From one lighthouse, a ship appears at 30° from the line to the other lighthouse. From the second lighthouse, the same ship appears at 45°. How far is the ship from each lighthouse?
Solution: Use the Law of Sines to set up proportions and solve for the unknown distances.
Example 3: A tree casts a shadow 20m long when the sun is at 60° elevation. How tall is the tree?
Solution: This forms a right triangle, but we can still use the Law of Sines to solve it.
Practice Tip
Draw the triangle and label all known measurements before setting up your Law of Sines equation.
Law of Sines Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the Law of Sines:
Math Trivia
Discover interesting facts about triangles and trigonometry:
Ancient Origins
The Law of Sines was known to medieval Persian and Indian mathematicians, but it was first properly stated in Europe by the 15th century German mathematician Johann Müller.
Navigation Uses
The Law of Sines is essential in celestial navigation, helping sailors determine their position at sea by measuring angles between stars and the horizon.
Space Applications
NASA engineers use the Law of Sines to calculate trajectories and distances in space missions, especially when dealing with triangular relationships between spacecraft, planets, and stars.
Triangle Records
The largest triangle ever drawn was created in 2016 in Dubai, with sides measuring 1.2 km, 1.6 km, and 2.0 km. Surveyors used the Law of Sines to verify its angles!





