Like Numerators - Definition, Examples, Quiz, FAQ, Trivia
Learn to identify, compare, and order fractions with the same numerator through easy explanations and practice activities
What Are Like Numerators?
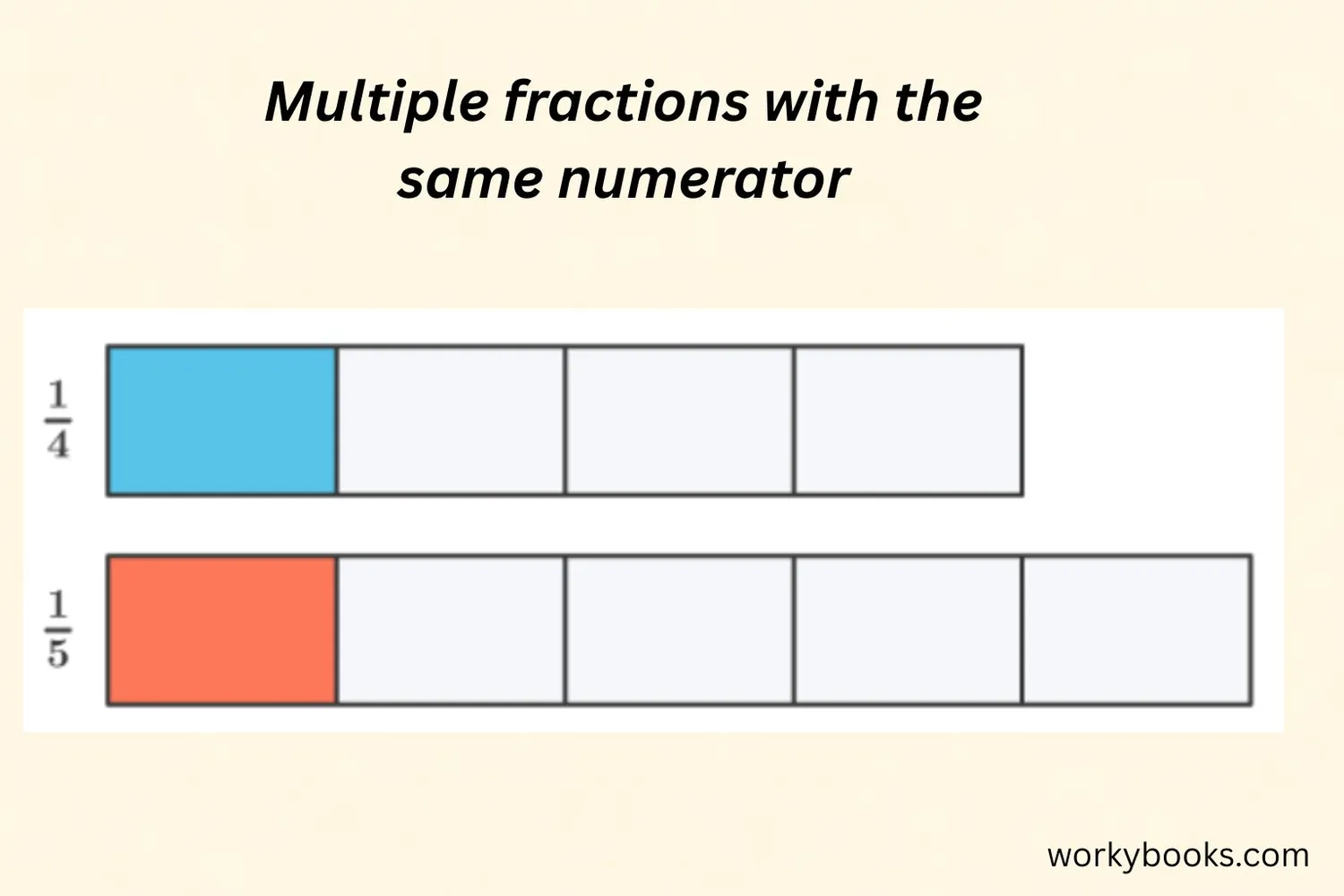
Fractions have two parts: the numerator (top number) and the denominator (bottom number).
Like numerators are fractions that have the same number on top but different numbers on the bottom.
For example, these fractions all have like numerators:
All these fractions have the numerator 3, so they have like numerators. The denominators are different (4, 5, and 8).
When fractions have like numerators, we can compare them by looking at their denominators. The fraction with the smaller denominator represents a larger value.
Key Concept
Fractions with like numerators have the same top number but different bottom numbers.
Comparing Fractions with Like Numerators
When fractions have the same numerator, we can compare them by looking at their denominators.
Comparison Rule
When numerators are the same, the fraction with the smaller denominator is larger.
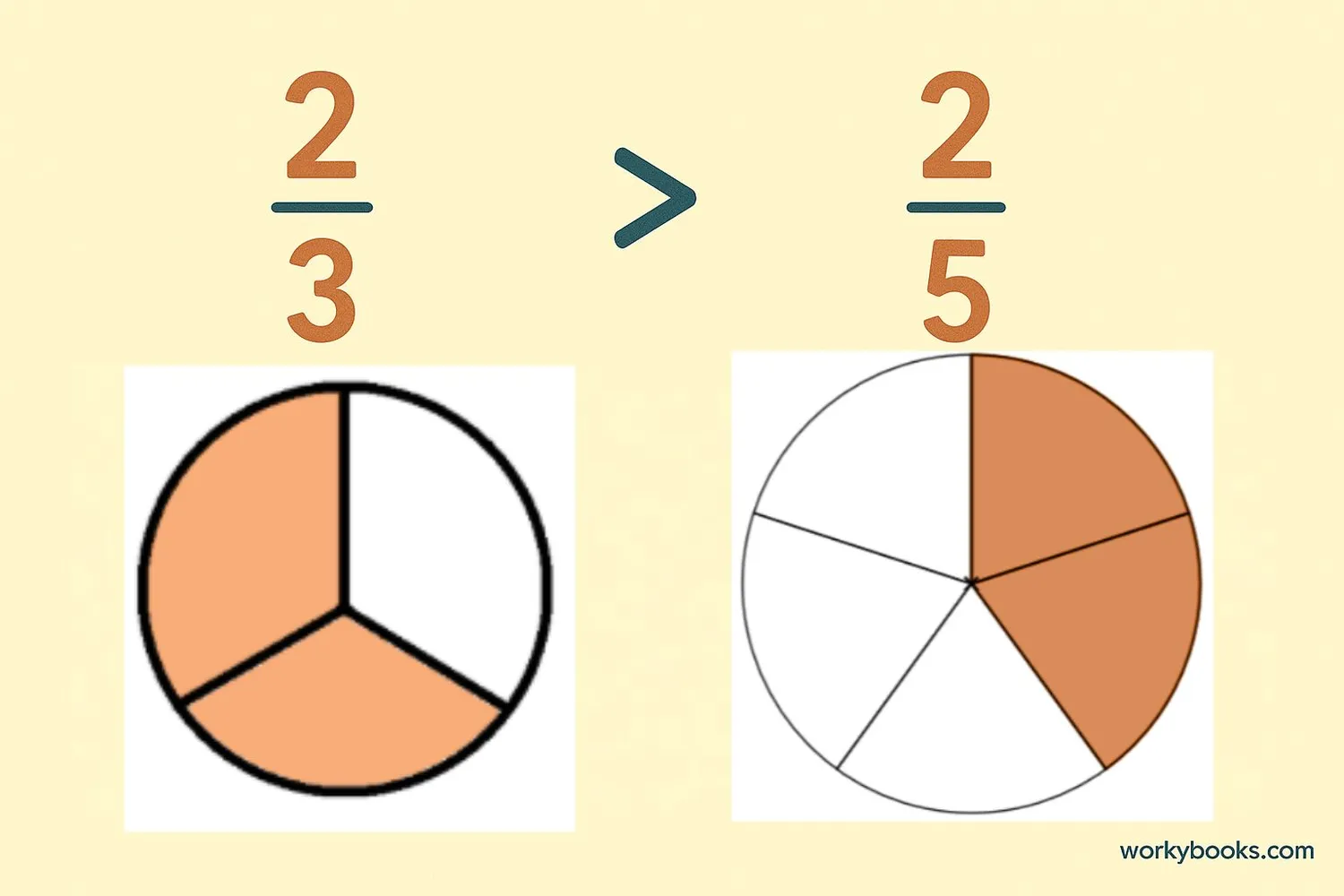
Example: Compare 2/3 and 2/5
Step 1: Notice that both fractions have the same numerator (2)
Step 2: Compare denominators: 3 vs. 5
Step 3: Since 3 is smaller than 5, 2/3 is larger than 2/5
Why does this work? Think about sharing a pizza. If you have 2 slices from a pizza cut into 3 pieces, you have more pizza than if you have 2 slices from a pizza cut into 5 pieces.
Remember
When numerators are the same, the fraction with the smaller denominator represents larger pieces, so it's a larger fraction.
Ordering Fractions with Like Numerators
Ordering fractions with like numerators follows the same rule as comparing them.
To order fractions with like numerators from least to greatest:
1. Identify that the numerators are the same
2. Order the denominators from largest to smallest
3. The fractions will be ordered from smallest to largest
Let's practice with an example:
Example: Order 3/4, 3/8, and 3/5 from least to greatest
Step 1: All fractions have numerator 3 (like numerators)
Step 2: Look at denominators: 4, 8, and 5
Step 3: Order denominators from largest to smallest: 8, 5, 4
Step 4: The fractions from least to greatest: 3/8, 3/5, 3/4
Why is this correct? With the same numerator, the fraction with the largest denominator has the smallest pieces, so it's the smallest fraction.
Ordering Tip
When ordering fractions with like numerators, think "larger denominator = smaller fraction."
Real-World Examples

Let's see how like numerators work in real life:
Example 1: Pizza slices
You have 2 slices from a small pizza cut into 4 pieces (2/4) and 2 slices from a large pizza cut into 8 pieces (2/8).
Which gives you more pizza? Since 4 is smaller than 8, 2/4 is larger than 2/8.
Example 2: Chocolate bars
You have 3 pieces from a chocolate bar divided into 6 sections (3/6) and 3 pieces from a chocolate bar divided into 8 sections (3/8).
Which is more chocolate? Since 6 is smaller than 8, 3/6 is larger than 3/8.
Example 3: Measuring cups
You have 2/3 cup of flour and 2/5 cup of sugar. Which is more?
Since 3 is larger than 5, 2/3 is smaller than 2/5? Wait, let's think again!
Actually, since 3 is smaller than 5, 2/3 is larger than 2/5. So you have more flour than sugar.
Practice looking for fractions in your daily life and see if they have like numerators!
Real-World Tip
When the numerator stays the same, smaller denominators mean larger pieces, so you get more of the whole.
Fractions Practice Quiz
Test your understanding of fractions with like numerators with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about fractions with like numerators:
Fraction Trivia
Discover interesting facts about fractions and mathematics:
Ancient Fractions
The ancient Egyptians used fractions as early as 1800 BC. They mainly used unit fractions (fractions with 1 as the numerator) and would write other fractions as sums of unit fractions.
Word Origins
The word "numerator" comes from the Latin word "numerātor" which means "counter." The word "denominator" comes from "dēnōminātor" which means "namer."
Fractions in Music
Musical notes are based on fractions! A whole note can be divided into half notes, quarter notes, eighth notes, and sixteenth notes - all fractions of the whole.
Infinite Fractions
Between any two fractions, no matter how close they are, there are infinitely many other fractions. This property is called density of rational numbers.





