Line of Symmetry - Definition, Examples, Quiz, FAQ, Trivia
Learn about symmetry in shapes with easy explanations, examples, and practice activities
What is a Line of Symmetry?

A line of symmetry is an imaginary line that divides a shape or object into two identical halves. When you fold a shape along its line of symmetry, both sides match perfectly. Think of it like a mirror placed in the middle of a shape - one side is the reflection of the other.
Symmetry is all around us in nature, art, and everyday objects. Butterflies, leaves, and even our faces have symmetry. Understanding symmetry helps us recognize patterns and create balanced designs.
Key Concept
A line of symmetry divides a shape into two mirror-image halves. If you fold along this line, both sides match perfectly.
Types of Symmetry
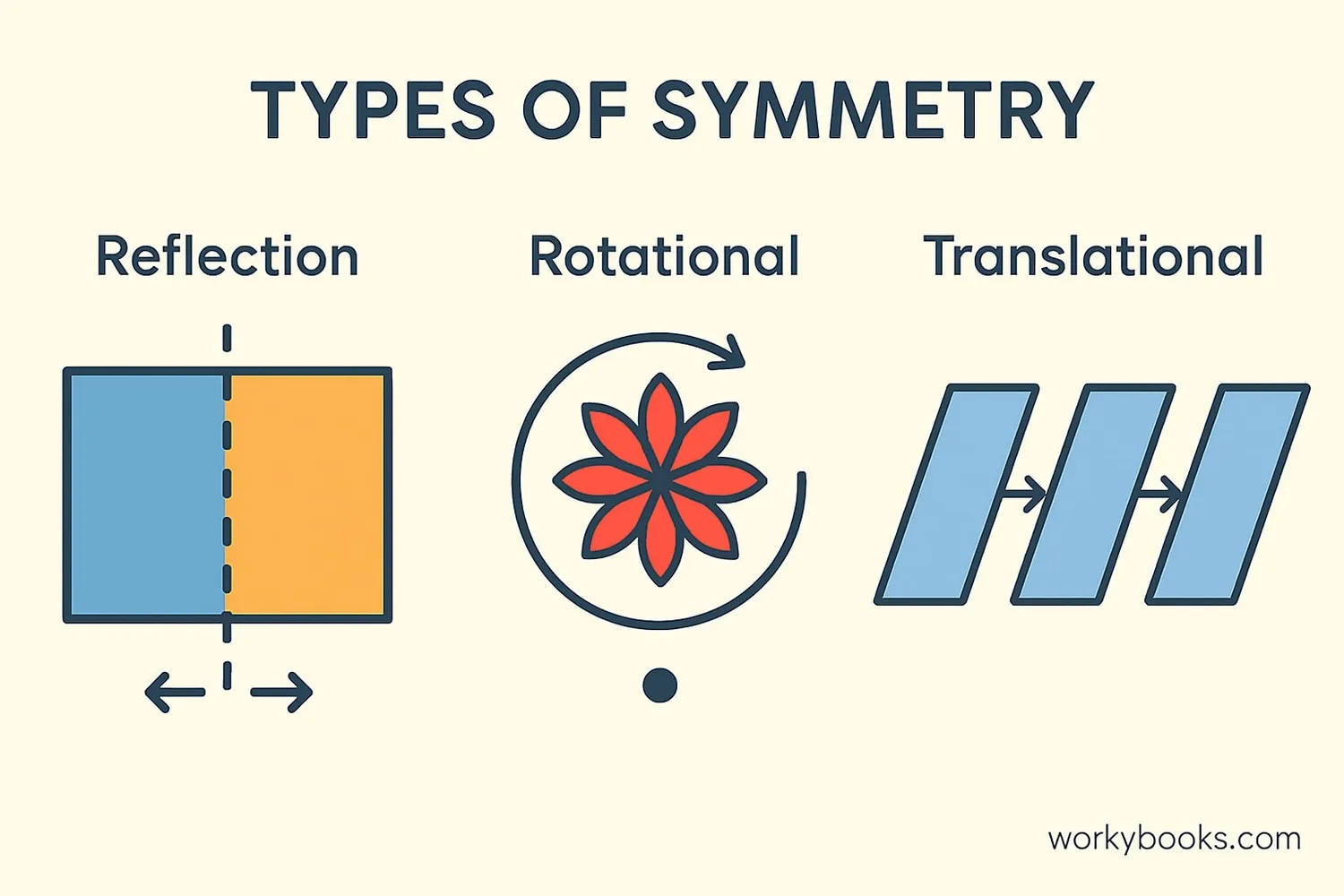
There are several types of symmetry, but the two main types we'll focus on are:
Reflection Symmetry (Line Symmetry): This is the most common type. A shape has reflection symmetry if it can be divided by a line into two parts that are mirror images of each other.
Rotational Symmetry: A shape has rotational symmetry if it can be rotated (turned) around a central point and still look the same in more than one position.
Some shapes have both types of symmetry! A circle has infinite lines of symmetry and also rotational symmetry.
Reflection Symmetry
Rotational Symmetry
Remember
Reflection symmetry is like a mirror, while rotational symmetry is like turning a shape around a center point.
Examples of Lines of Symmetry
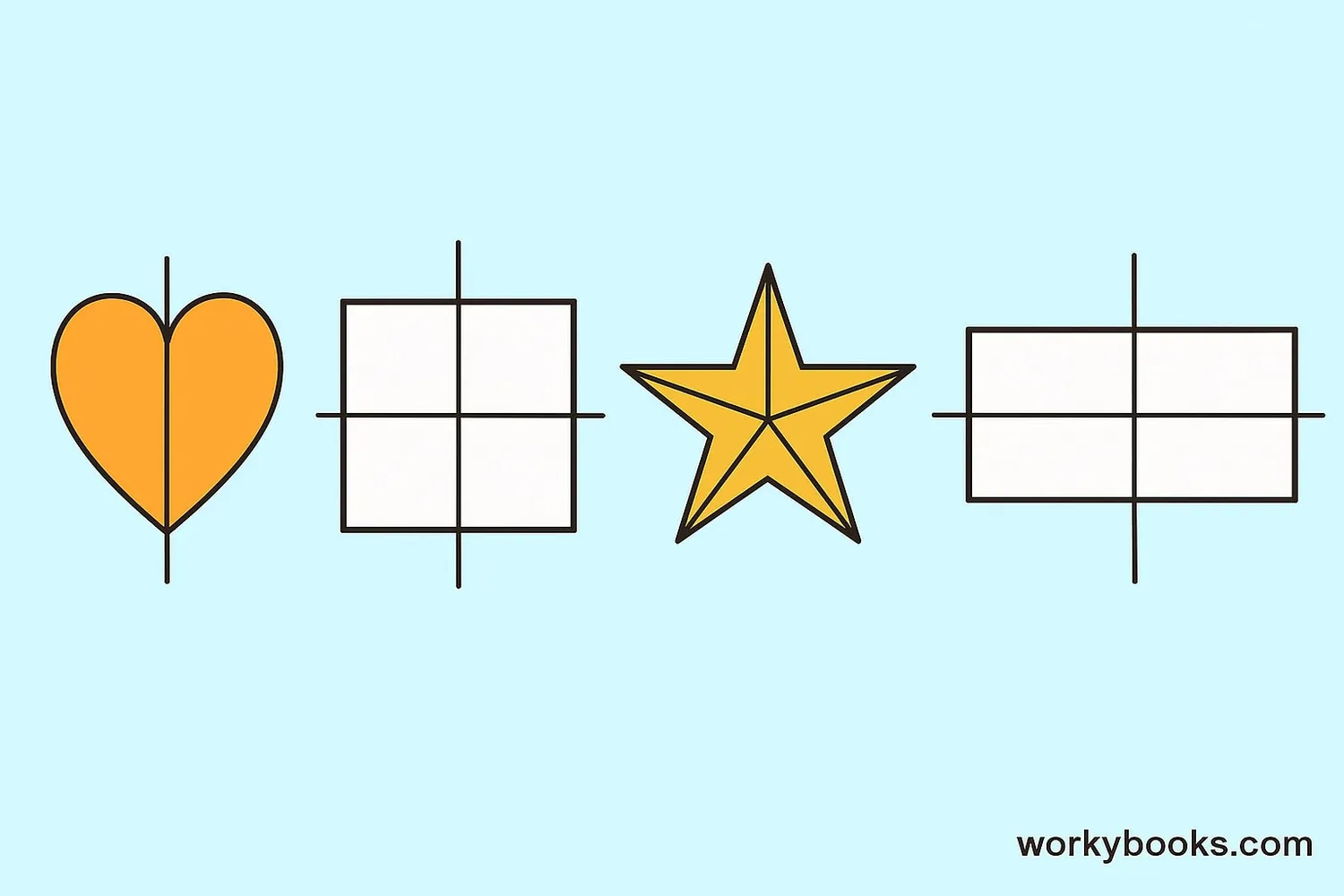
Let's look at some examples of shapes and their lines of symmetry:
Square: A square has 4 lines of symmetry - one vertical, one horizontal, and two diagonal.
Rectangle: A rectangle has 2 lines of symmetry - one vertical and one horizontal.
Circle: A circle has infinite lines of symmetry! Any line that passes through its center is a line of symmetry.
Heart: A heart shape has only 1 line of symmetry down its center.
Equilateral Triangle: An equilateral triangle has 3 lines of symmetry - one from each vertex to the midpoint of the opposite side.
Try This
Look around your room. Can you find objects with lines of symmetry? A book, a window, or maybe a clock?
Shapes & Their Lines of Symmetry
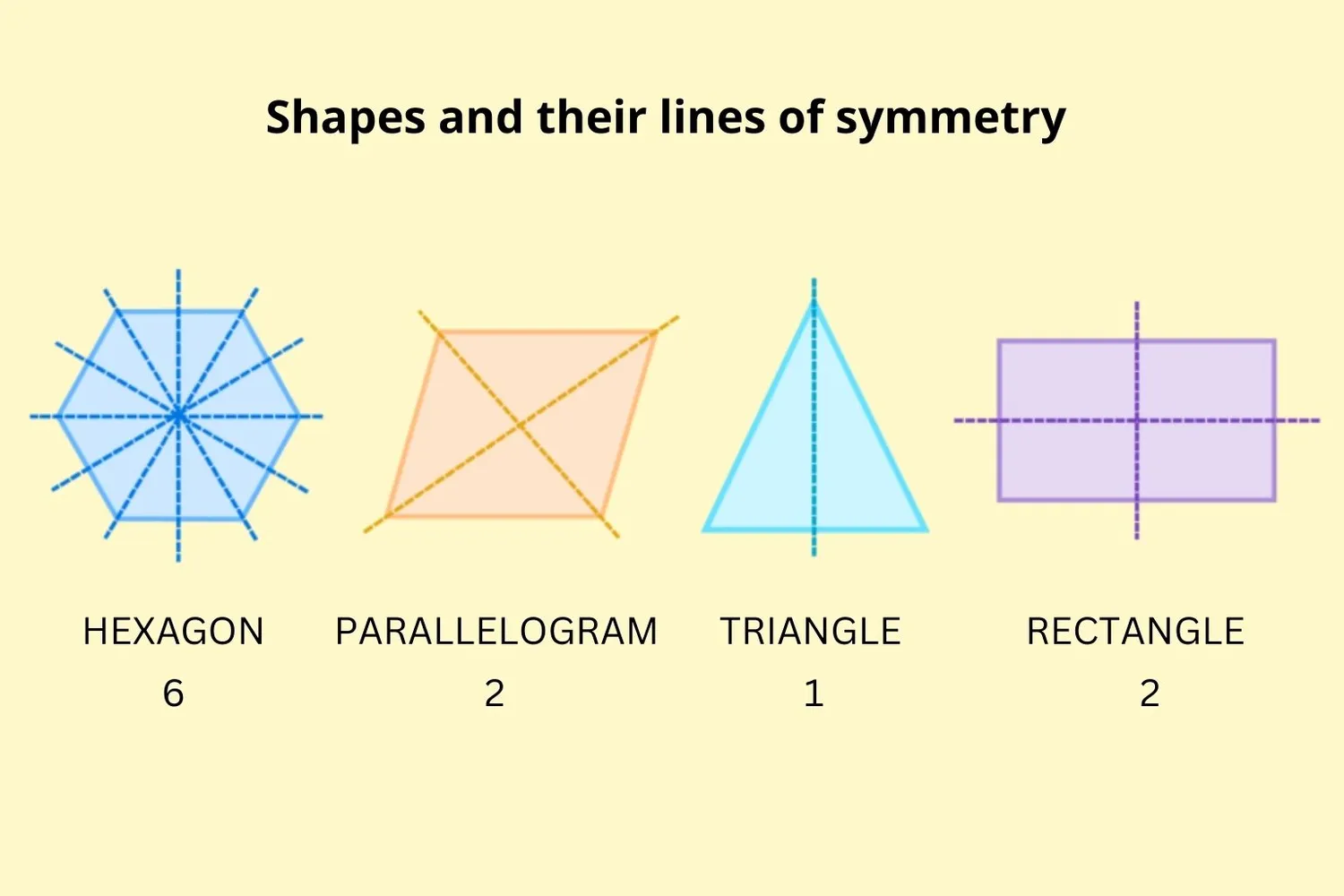
Different shapes have different numbers of lines of symmetry. Regular polygons (shapes with equal sides and angles) have as many lines of symmetry as they have sides.
Lines of Symmetry in Common Shapes
| Shape | Number of Lines of Symmetry | Description |
|---|---|---|
| Scalene Triangle | 0 | No equal sides or angles |
| Isosceles Triangle | 1 | Two equal sides |
| Equilateral Triangle | 3 | All sides and angles equal |
| Rectangle | 2 | Opposite sides equal |
| Square | 4 | All sides equal, all angles 90° |
| Regular Pentagon | 5 | 5 equal sides and angles |
| Regular Hexagon | 6 | 6 equal sides and angles |
| Circle | Infinite | All diameters are lines of symmetry |
Pattern Notice
Regular polygons have the same number of lines of symmetry as they have sides. A regular octagon has 8 lines of symmetry!
Symmetry Practice Quiz
Test your knowledge about lines of symmetry with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about lines of symmetry:
Symmetry Trivia
Discover interesting facts about symmetry:
Symmetry in Nature
Most animals have bilateral symmetry, meaning their left and right sides are mirror images. Flowers often have radial symmetry, with petals arranged equally around the center.
Human Symmetry
Human faces are almost symmetrical, but not perfectly. Small differences between the left and right sides make each face unique. This slight asymmetry is often what makes faces interesting!
Symmetry in Architecture
Famous buildings like the Taj Mahal and the Parthenon were designed with perfect symmetry. This creates a sense of balance, harmony, and grandeur that we find visually appealing.
Infinite Symmetry
A circle has infinite lines of symmetry because any line through its center will divide it into equal halves. This makes it the most symmetric of all two-dimensional shapes.





