Lines of Symmetry in a Rectangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about symmetry in rectangles with easy explanations, visual examples, and practice activities
What is a Line of Symmetry?
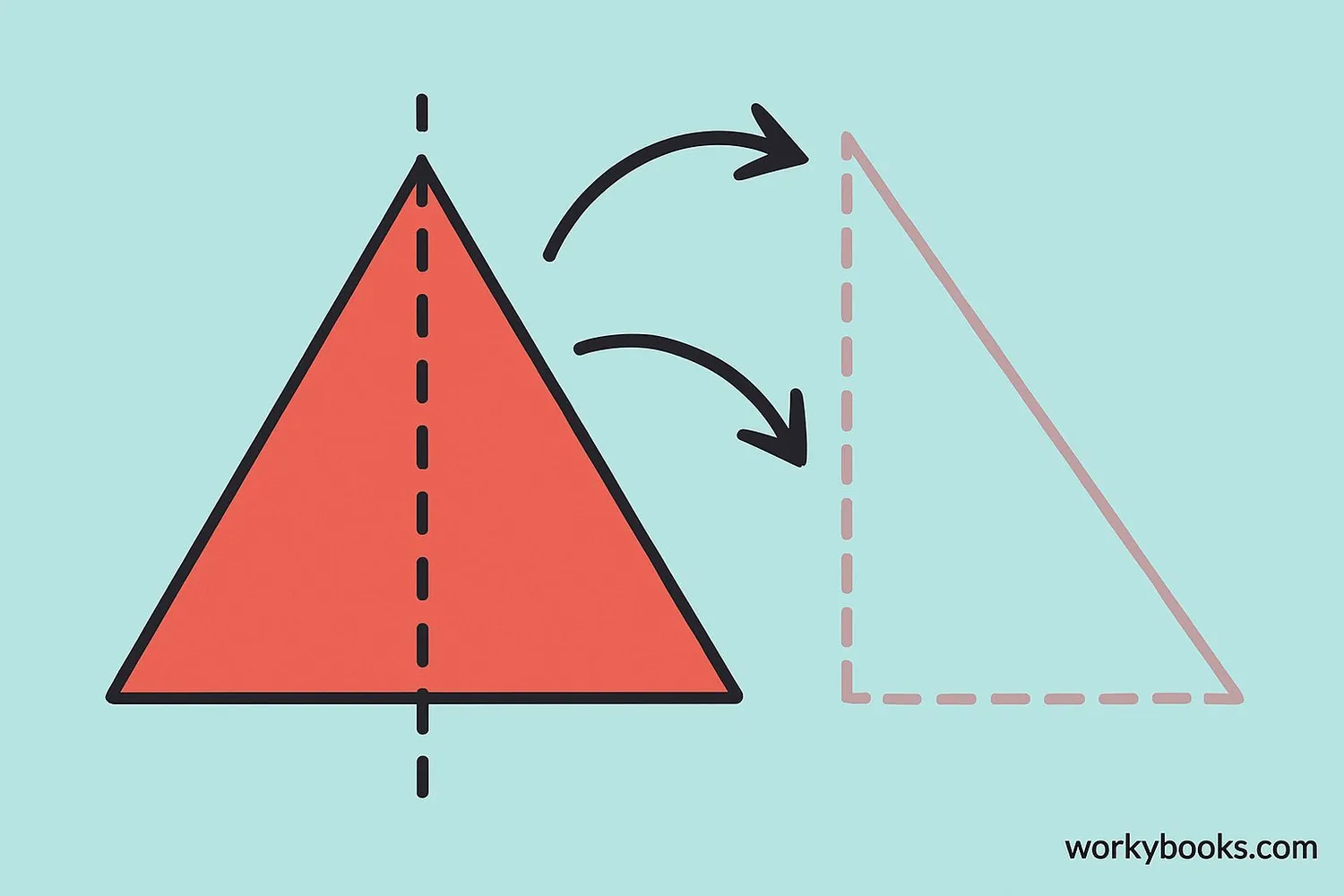
A line of symmetry is an imaginary line that divides a shape into two identical parts. When you fold a shape along its line of symmetry, the two halves match exactly.
Think of symmetry like a mirror - one side is a reflection of the other. Many objects in nature have symmetry, like leaves, butterflies, and human faces.
In geometry, we study symmetry to understand how shapes are organized and how they can be transformed while maintaining their essential properties.
Key Concept
A line of symmetry divides a shape into two mirror-image halves that are exactly the same size and shape.
Lines of Symmetry in a Rectangle
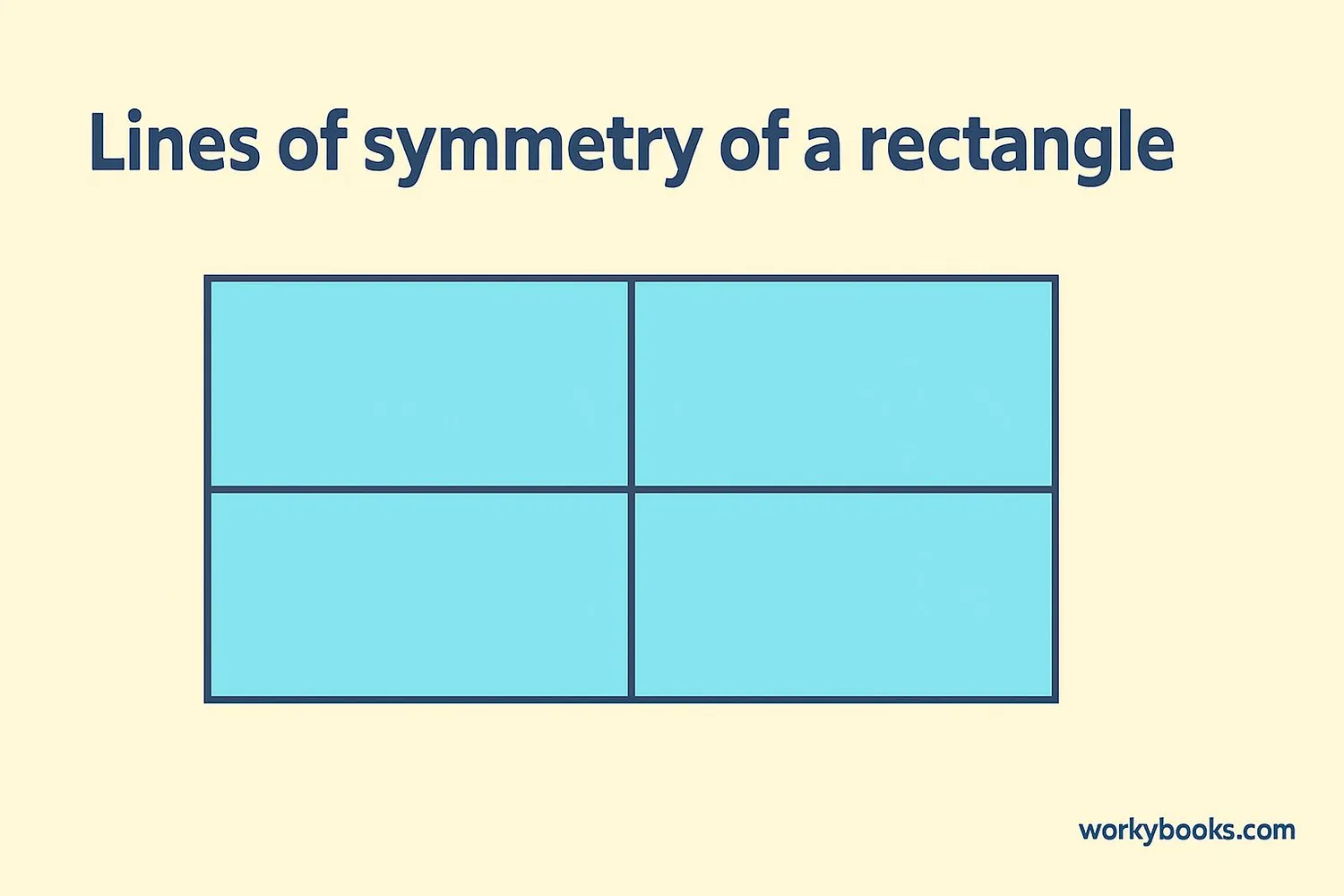
A rectangle has exactly two lines of symmetry. These lines run through the center of the rectangle:
1. One line runs horizontally through the middle, dividing the rectangle into top and bottom halves.
2. The other line runs vertically through the middle, dividing the rectangle into left and right halves.
These lines are called the lines of symmetry because if you fold the rectangle along either line, the two halves will match perfectly.
Important Fact
Unlike a square, a rectangle does not have diagonal lines of symmetry.
Remember
All rectangles have exactly two lines of symmetry, regardless of their size, as long as they're not squares.
Rotational Symmetry of a Rectangle

Rotational symmetry is when a shape looks the same after being rotated by a certain angle around its center point.
A rectangle has rotational symmetry of order 2. This means:
- When you rotate a rectangle by 180 degrees (half a full turn), it looks exactly the same as the original.
- After a full 360-degree rotation, the rectangle returns to its original position.
The order of rotational symmetry (2) tells us how many times the shape matches its original position during a full rotation.
Rotation Tip
Try this with a rectangular piece of paper: rotate it 180 degrees and notice it looks the same as before!
Rectangle vs Square Symmetry
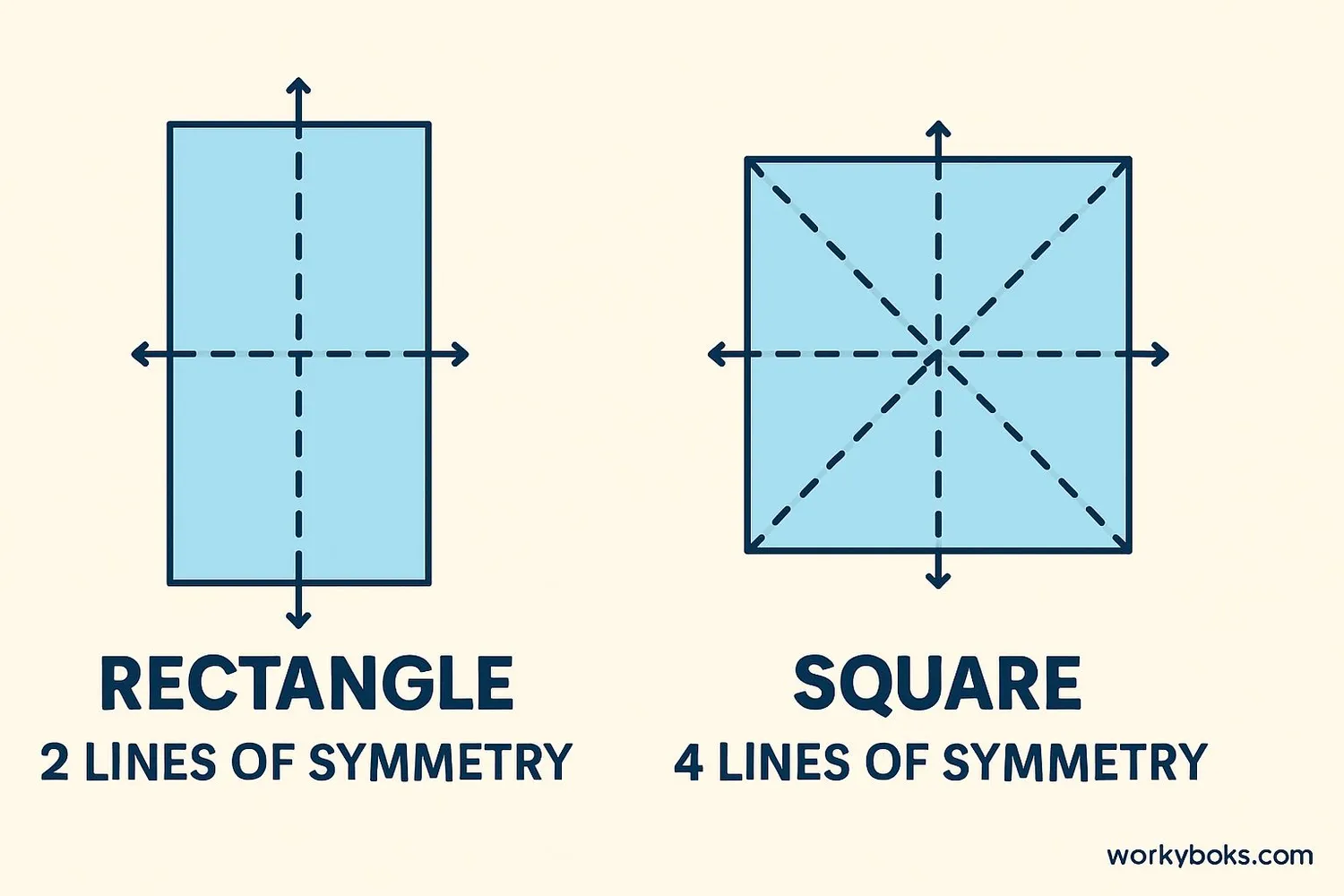
While rectangles and squares are both quadrilaterals with four right angles, they have different symmetry properties:
Rectangle:
- 2 lines of symmetry (horizontal and vertical through center)
- Rotational symmetry of order 2
Square:
- 4 lines of symmetry (horizontal, vertical, and two diagonals)
- Rotational symmetry of order 4
The key difference is that a square has additional diagonal lines of symmetry and higher rotational symmetry because all its sides are equal.
Symmetry Comparison Table
| Property | Rectangle | Square |
|---|---|---|
| Lines of Symmetry | 2 | 4 |
| Rotational Symmetry | Order 2 | Order 4 |
| Diagonal Symmetry | No | Yes |
Remember
A square is a special type of rectangle that has all sides equal, which gives it more lines of symmetry.
Symmetry Practice Quiz
Test your understanding of symmetry in rectangles with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about symmetry in rectangles:
Geometry Trivia
Discover interesting facts about symmetry and geometry:
Ancient Symmetry
The concept of symmetry has been studied since ancient times. The Greeks were particularly fascinated by symmetry and used it extensively in their architecture and art.
Symmetry in Nature
Symmetry is everywhere in nature! From snowflakes with 6 lines of symmetry to butterflies with bilateral symmetry, natural patterns often follow symmetrical arrangements.
Mathematical Beauty
Mathematicians study symmetry through a field called "group theory." This advanced mathematics helps describe and classify all possible types of symmetry in shapes and patterns.
Symmetry in Architecture
Many famous buildings, like the Taj Mahal and the Parthenon, use symmetry in their design. Symmetry creates a sense of balance and beauty that humans naturally find appealing.





