Midsegment of a Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn about triangle midsegments with easy explanations, interactive diagrams, and practice activities
What is a Midsegment of a Triangle?
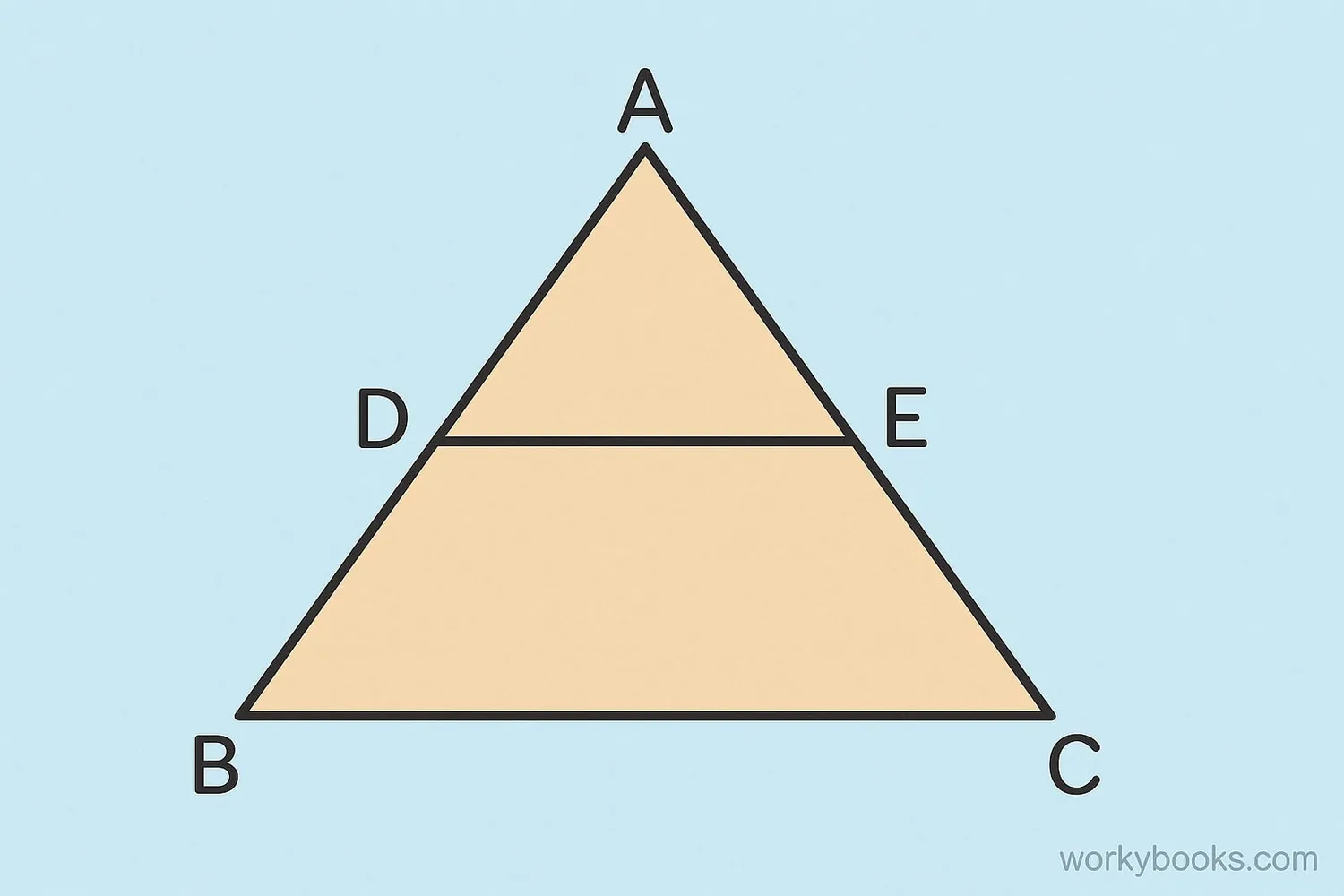
A midsegment of a triangle is a segment that connects the midpoints of two sides of the triangle. Every triangle has three midsegments, which form a smaller triangle inside the original triangle.
To find a midsegment:
1. Find the midpoint of two sides of the triangle
2. Connect these two midpoints with a segment
The midsegment is always parallel to the third side of the triangle, and it's exactly half as long as that side. This special relationship is called the Triangle Midsegment Theorem.
Key Concept
A midsegment connects the midpoints of two sides of a triangle. It is parallel to the third side and half its length.
The Midsegment Theorem
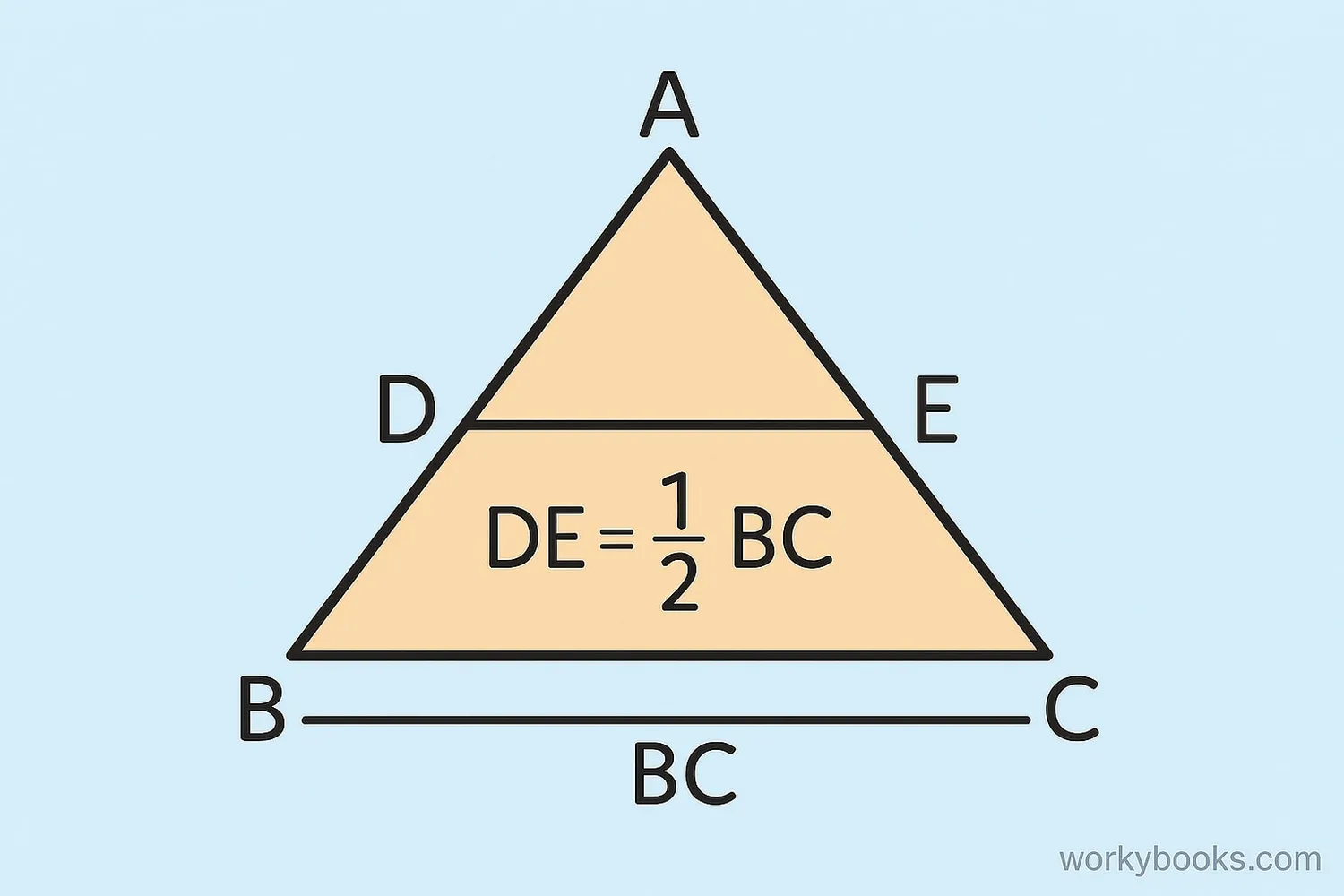
The Triangle Midsegment Theorem states that:
Midsegment Theorem
The midsegment is parallel to the third side and half its length.
Example: In triangle ABC, if side BC is 10 cm long, and D and E are the midpoints of AB and AC respectively, then:
- DE will be parallel to BC
- DE will be exactly 5 cm long (half of 10 cm)
This theorem works for all types of triangles: acute, right, and obtuse triangles.
Remember
The midsegment is always parallel to the third side and always exactly half its length, no matter what type of triangle you have.
Properties of Midsegments
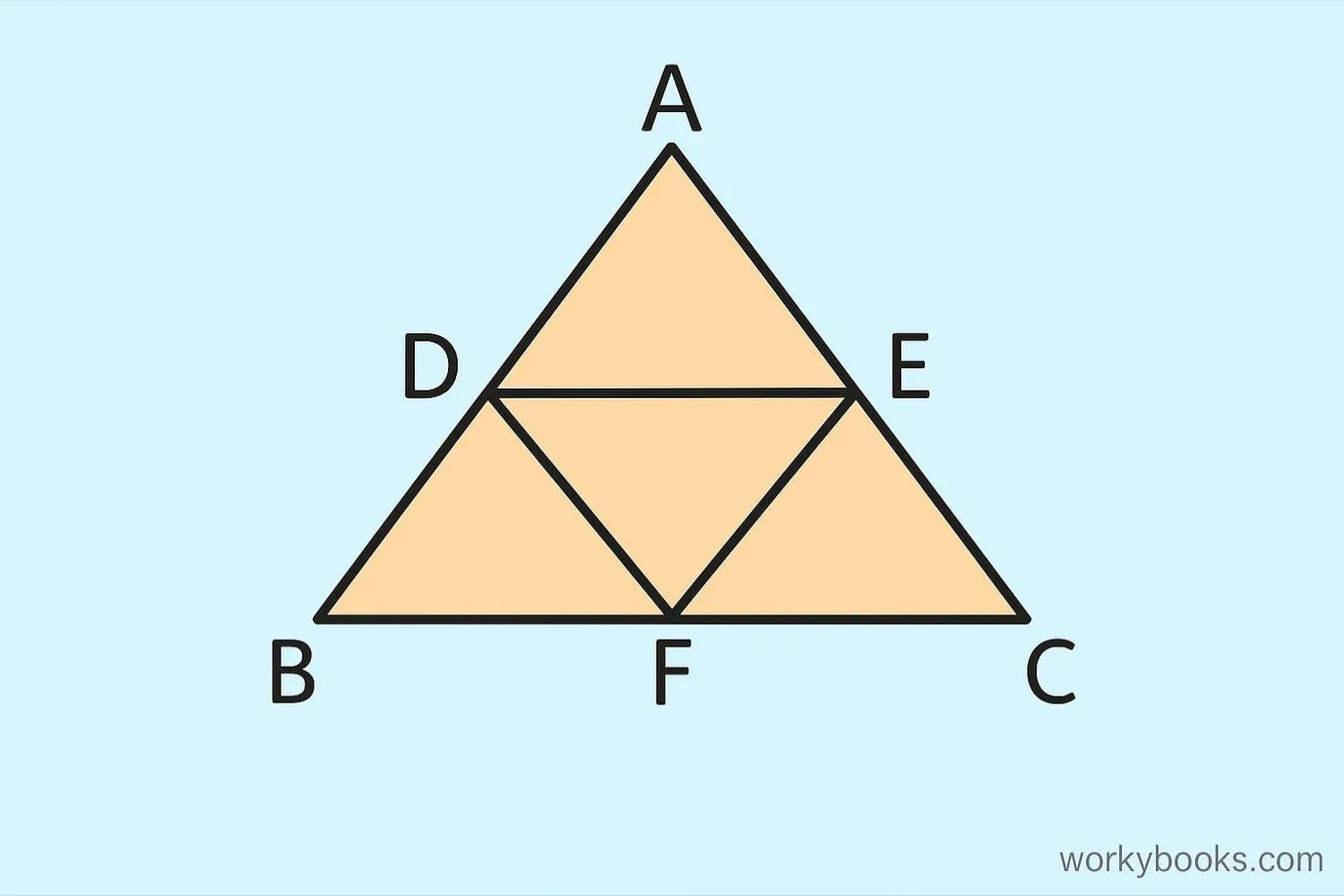
Midsegments have several important properties:
Key Properties
| Property | Description |
|---|---|
| Parallelism | Each midsegment is parallel to the third side of the triangle |
| Length | Each midsegment is half the length of the side it's parallel to |
| Medial Triangle | The three midsegments form a smaller triangle called the medial triangle |
| Similarity | The medial triangle is similar to the original triangle |
| Area | The medial triangle has one-fourth the area of the original triangle |
Relationship with Other Elements
| Element | Relationship with Midsegment |
|---|---|
| Medians | Midsegments and medians intersect at different points |
| Altitude | Midsegments maintain the same orientation as the original triangle |
| Angle Bisectors | The medial triangle has its own angle bisectors |
Interesting Fact
The medial triangle (formed by the three midsegments) is always similar to the original triangle, with a ratio of 1:2.
Real-World Examples
Let's see how midsegments work in practice:
Example 1: In triangle ABC, side BC is 16 cm. If D and E are midpoints of AB and AC, how long is midsegment DE?
Solution: According to the Midsegment Theorem, DE = ½ × BC = ½ × 16 = 8 cm
Example 2: A triangular park has paths connecting the midpoints of its sides. If the sides of the park are 120m, 150m, and 200m, what are the lengths of the paths?
Solution: Each path (midsegment) is half the length of the side it's parallel to:
- Path parallel to 120m side: 60m
- Path parallel to 150m side: 75m
- Path parallel to 200m side: 100m
Example 3: In triangle XYZ, the midsegment connecting the midpoints of XY and XZ is 7 inches long. How long is side YZ?
Solution: Since the midsegment is half the length of the side it's parallel to, YZ = 2 × 7 = 14 inches
Example 4: A triangular sail has a base of 20 feet. The reinforcement seam runs between the midpoints of the two other sides. How long is this seam?
Solution: The seam is a midsegment parallel to the base, so its length = ½ × 20 = 10 feet
Application Tip
Engineers often use the midsegment theorem in construction to create strong yet lightweight triangular supports in bridges and roofs.
Midsegment Practice Quiz
Test your understanding of triangle midsegments with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about triangle midsegments:
Geometry Trivia
Discover interesting facts about triangles and geometry:
Ancient Geometry
The study of triangles dates back to ancient Egypt and Babylon, where they were used in land surveying and construction. The Egyptians used ropes with equally spaced knots to create right triangles.
Triangle Facts
There are exactly 12 different types of triangles when classified by both side lengths (scalene, isosceles, equilateral) and angles (acute, right, obtuse).
Structural Strength
Triangles are the strongest geometric shape for construction because they distribute weight evenly. This is why you see triangles in bridges, towers, and roof supports.
Triangles in Nature
Triangular patterns appear throughout nature, from the arrangement of leaves on some plants to the structure of crystals and honeycombs. Even some molecular structures form triangles.





