Obtuse Triangle - Definition, Examples, Quiz, FAQ, Trivia
Understanding Triangles with One Angle Greater Than 90 Degrees
What is an Obtuse Triangle?
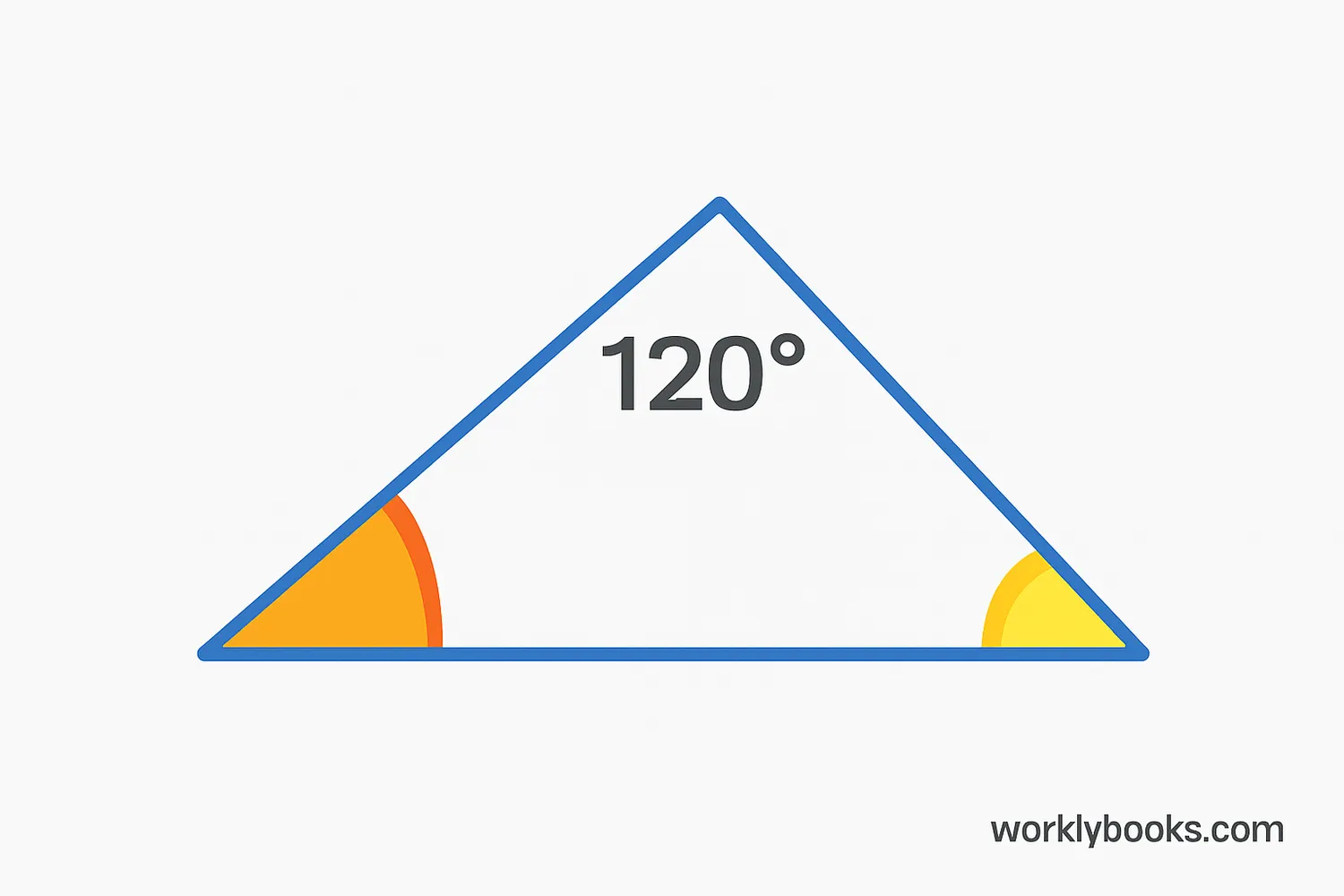
An obtuse triangle is a special type of triangle that has one angle greater than 90 degrees. The word "obtuse" means "blunt" or "not sharp," which describes this wide angle.
In any triangle, the three angles always add up to 180 degrees. In an obtuse triangle, one angle is between 90 and 180 degrees, while the other two angles are acute (less than 90 degrees).
Math Fact!
You can identify an obtuse triangle by looking for the "widest" angle. If one angle looks like it's "spread out" more than a right angle (like a corner of a book), you've found an obtuse triangle!
Properties of Obtuse Triangles
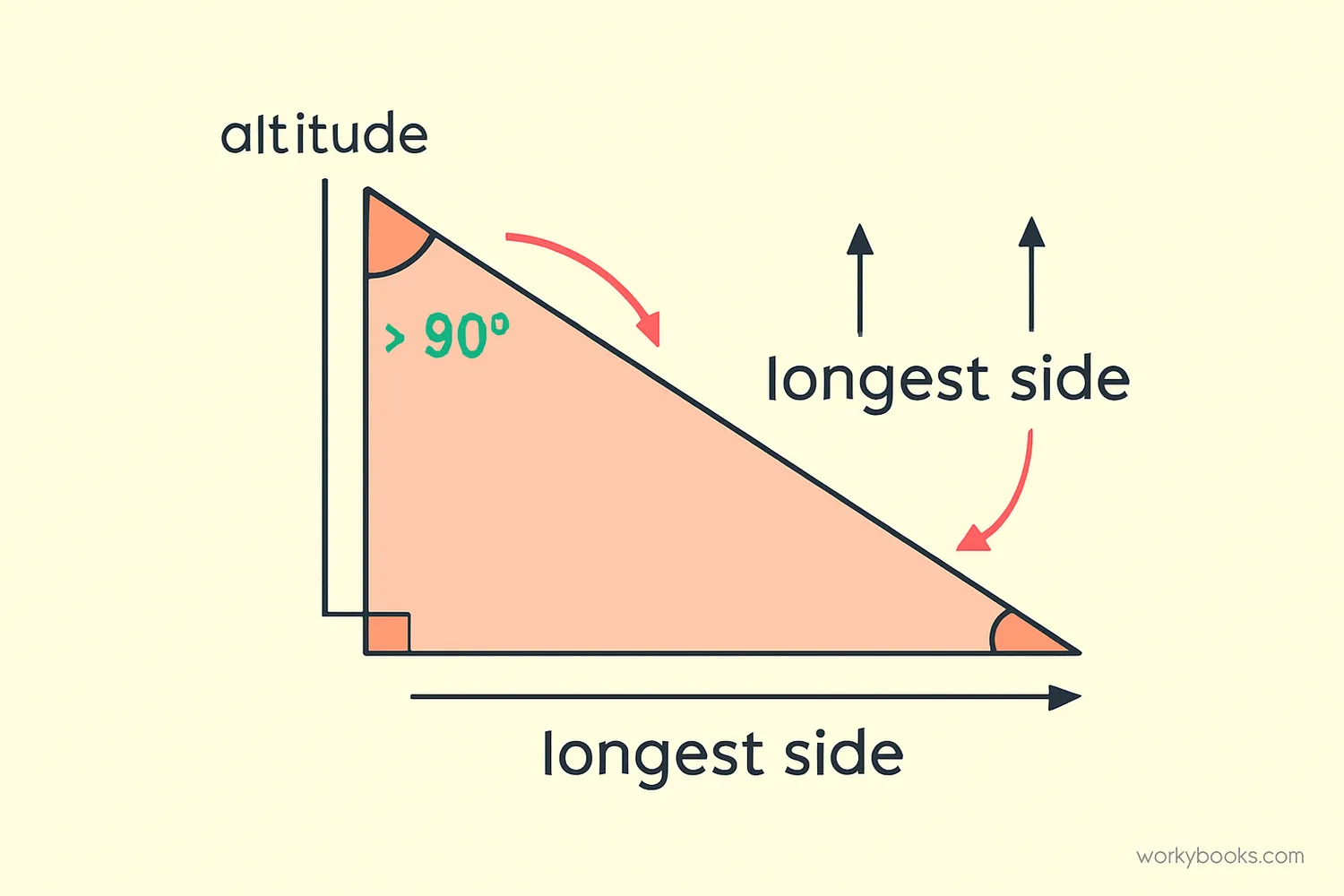
Obtuse triangles have some interesting properties that make them special:
One Obtuse Angle
Exactly one angle measures between 90° and 180°
Longest Side
The side opposite the obtuse angle is the longest side
Two Acute Angles
The other two angles are always less than 90°
Altitude Outside
The altitude from the obtuse angle falls outside the triangle
Another important property is that in an obtuse triangle, the square of the longest side is greater than the sum of the squares of the other two sides. This is the opposite of the Pythagorean theorem for right triangles!
Types of Triangles
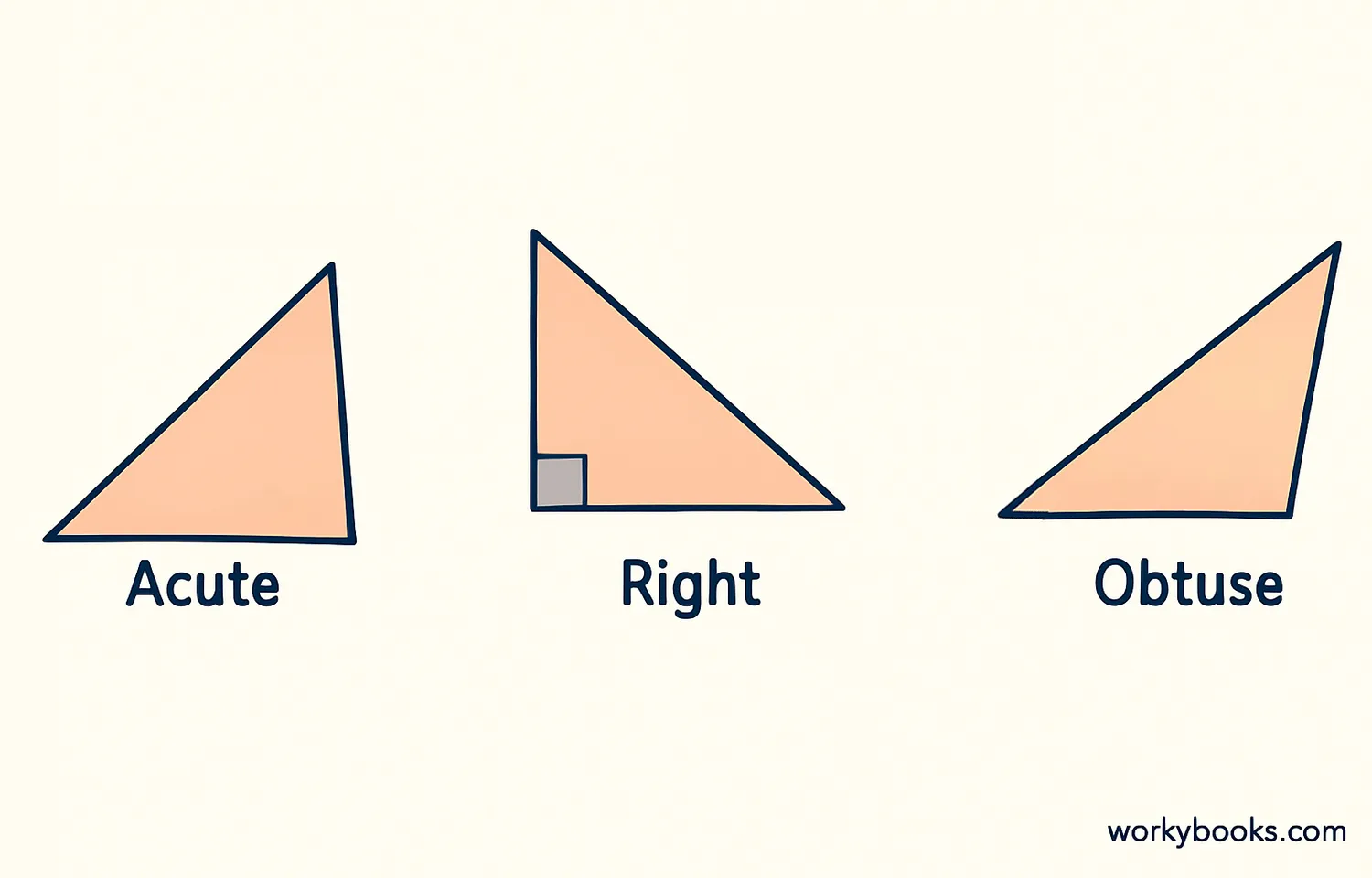
Triangles are classified based on their angles into three main types:
Acute Triangle
All three angles are less than 90°
Right Triangle
One angle is exactly 90°
Obtuse Triangle
One angle is greater than 90°
Triangles can also be classified by their sides (equilateral, isosceles, scalene). An obtuse triangle can be either isosceles (two equal sides) or scalene (no equal sides), but it can never be equilateral because all angles in an equilateral triangle are 60°.
Area of an Obtuse Triangle
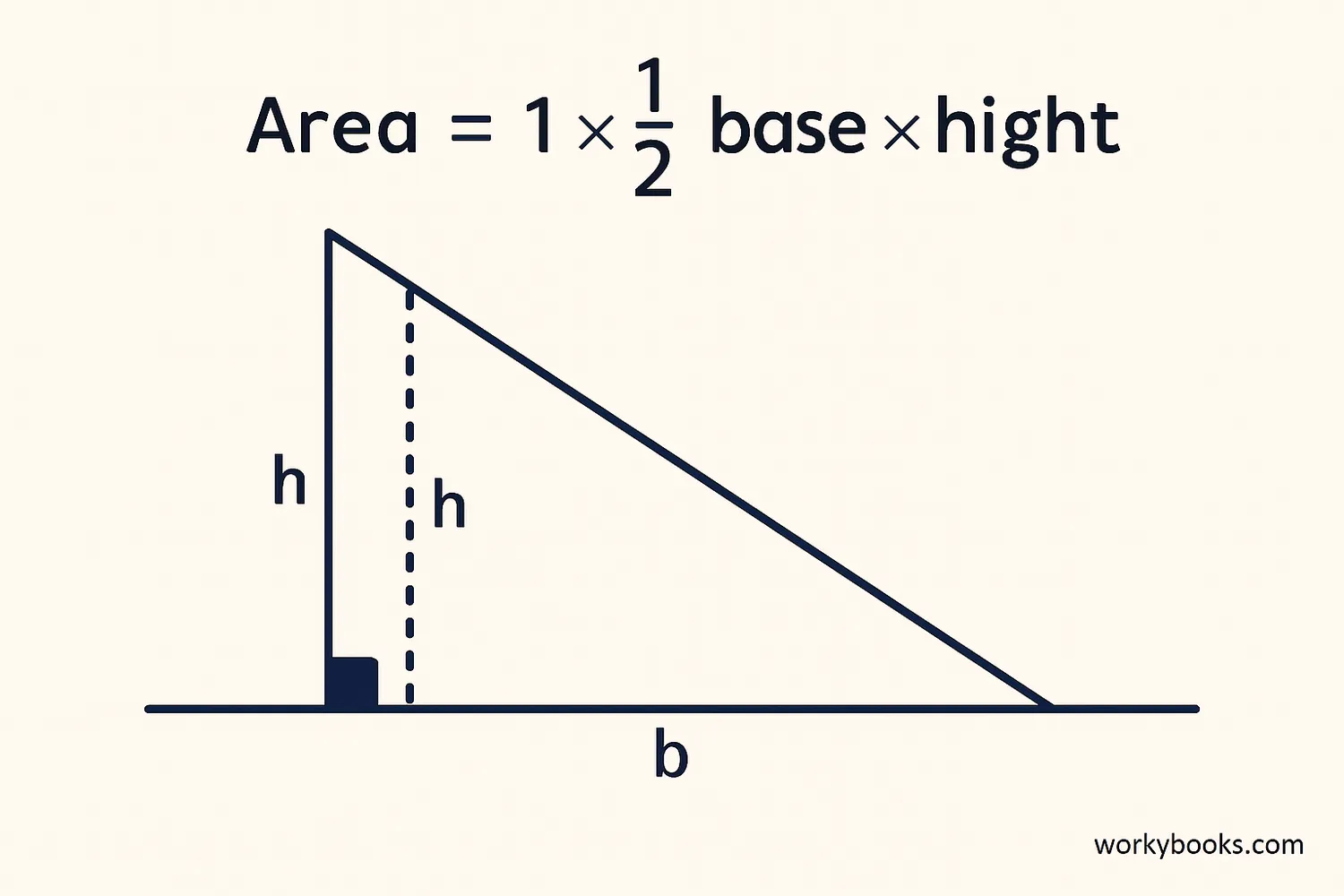
The area of an obtuse triangle is calculated the same way as any other triangle:
Area = 1/2 × base × height
The tricky part is that the height might fall outside the triangle when the obtuse angle is at the base. You might need to extend the base line to draw the altitude perpendicular to it.
Choose a Base
Select any side to be the base
Find the Height
Draw a perpendicular line from the opposite vertex to the base (or extended base)
Apply Formula
Multiply base × height, then divide by 2
Remember that the height is always perpendicular to the base, even if it falls outside the triangle. This is a special property of obtuse triangles!
Example
If an obtuse triangle has a base of 8 cm and a height of 5 cm, its area would be: 1/2 × 8 × 5 = 20 cm².
Obtuse Triangle Quiz
Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned about obtuse triangles.
Frequently Asked Questions
Here are answers to some common questions about obtuse triangles:
Math Facts About Obtuse Triangles
Discover some fascinating facts about obtuse triangles and geometry!
Triangle Classification
Triangles are the only polygons that are always convex, meaning all their interior angles are less than 180 degrees. This is why an obtuse triangle can have only one angle between 90 and 180 degrees.
Historical Context
The study of triangles dates back to ancient civilizations. The Babylonians and Egyptians used triangles for land surveying and construction as early as 2000 BCE!
Real-World Examples
Obtuse triangles appear in many real-world structures. The iconic Sydney Opera House roof sections form obtuse triangles, and many roof trusses use obtuse triangles for stability.
Mathematical Property
In an obtuse triangle, the circumcenter (the center of the circle that passes through all three vertices) always lies outside the triangle. This is unique to obtuse triangles!





