Perimeter of a Triangle - Definition, Examples, Quiz, FAQ, Trivia
Learn to measure the boundary of triangles with simple formulas and practice activities
What is Perimeter?

The perimeter of a triangle is the total length of its boundary, which means the sum of all its sides. It's like measuring the distance around the triangle.
Imagine you're walking around a triangular garden. The perimeter would be the total distance you walk to go all the way around it.
To find the perimeter of any triangle, you add the lengths of all three sides together:
Perimeter Formula
Where a, b, and c are the lengths of the three sides
Key Concept
Perimeter measures the boundary length of a shape. For triangles, it's the sum of all three sides.
How to Find Perimeter
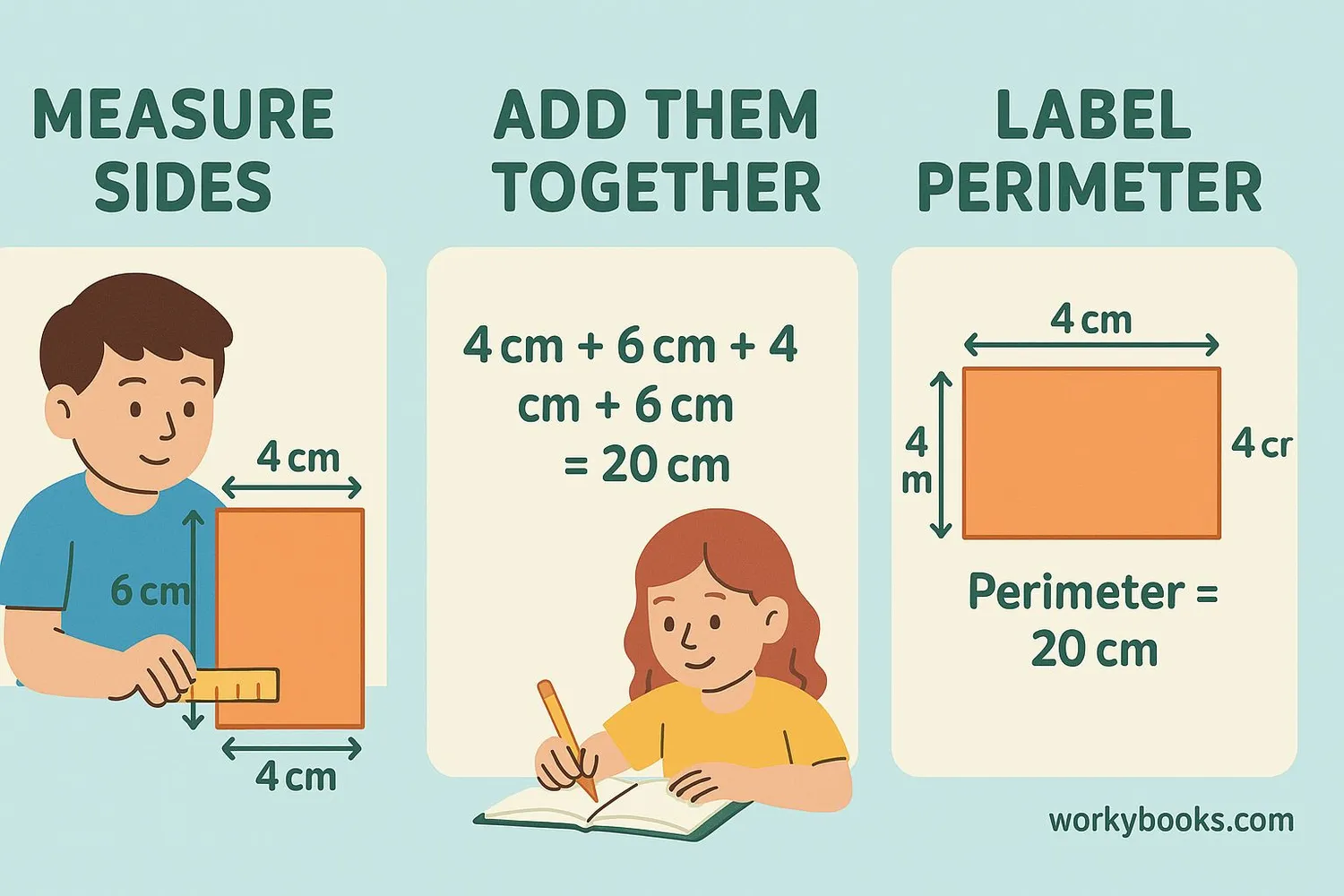
Finding the perimeter of a triangle is simple when you follow these steps:
Step 1: Identify the lengths of all three sides of the triangle. Make sure they're all in the same units (like centimeters or inches).
Step 2: Add the three lengths together.
Step 3: Write your answer with the correct units.
Let's try with a simple example:
Example: A triangle has sides of 5 cm, 7 cm, and 9 cm.
Perimeter = 5 + 7 + 9 = 21 cm
Remember
Perimeter is always measured in linear units like centimeters (cm), meters (m), or feet (ft).
Types of Triangles
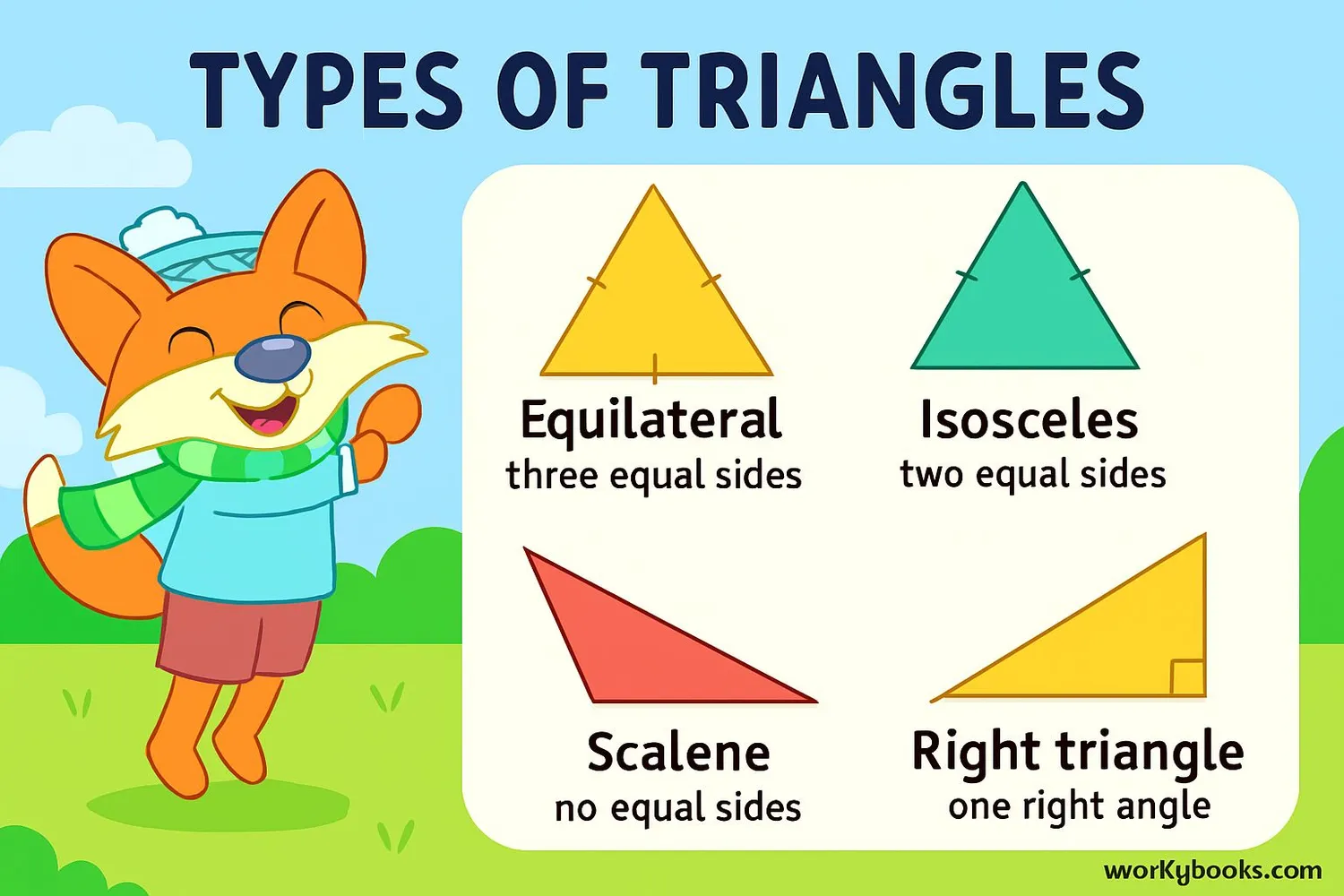
Different types of triangles have special properties that make calculating their perimeter easier:
Equilateral Triangle
All three sides equal
Example: Side = 5 cm
Perimeter = 3 × 5 = 15 cm
Isosceles Triangle
Two sides equal
Example: Equal sides = 6 cm, base = 4 cm
Perimeter = 2×6 + 4 = 16 cm
Scalene Triangle
All sides different
Example: Sides = 3cm, 4cm, 5cm
Perimeter = 3+4+5=12 cm
Right Triangle
One 90° angle
Use Pythagoras if needed:
c = √(a² + b²)
Special Case: Isosceles Right Triangle
For a right triangle with two equal legs (a), the hypotenuse is a√2. Perimeter = a + a + a√2 = 2a + a√2
Real-World Examples

Let's practice with some real-world examples:
Example 1: An equilateral triangular park has sides of 120 meters each. What is the perimeter?
Solution: Perimeter = 3 × 120 = 360 meters
Example 2: A triangular scarf has sides 45 cm, 45 cm, and 60 cm. What is its perimeter?
Solution: Perimeter = 45 + 45 + 60 = 150 cm
Example 3: A right triangular plot of land has legs of 9 meters and 12 meters. What is its perimeter?
Solution: First find hypotenuse: √(9² + 12²) = √(81 + 144) = √225 = 15 meters
Perimeter = 9 + 12 + 15 = 36 meters
Example 4: An isosceles triangle has perimeter 34 cm. If the two equal sides are 12 cm each, what is the base?
Solution: Perimeter = 2a + b
34 = 2×12 + b
34 = 24 + b
b = 34 - 24 = 10 cm
Practice Tip
Look for triangles around you - windows, signs, furniture. Estimate and calculate their perimeters!
Perimeter Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about triangle perimeter:
Triangle Trivia
Discover interesting facts about triangles:
Ancient Triangles
The ancient Egyptians used triangles over 4,000 years ago to survey land after Nile River floods. Their "rope stretchers" created perfect right triangles using ropes with 12 equally spaced knots.
Strongest Shape
Triangles are the strongest geometric shape because they distribute weight evenly. That's why you see triangles in bridges, roofs, and even the Eiffel Tower's structure!
Nature's Triangles
Triangles appear everywhere in nature - in crystal structures, honeycomb patterns, mountain peaks, and even the arrangement of leaves on some plants. They provide strength and efficiency.
Largest Triangle
The largest triangle ever created was made by astronomers! By connecting three distant quasars, they formed a triangle with sides measuring billions of light-years long.


