Perpendicular Bisector of a Chord - Definition, Examples, Quiz, FAQ, Trivia

What is a Chord?

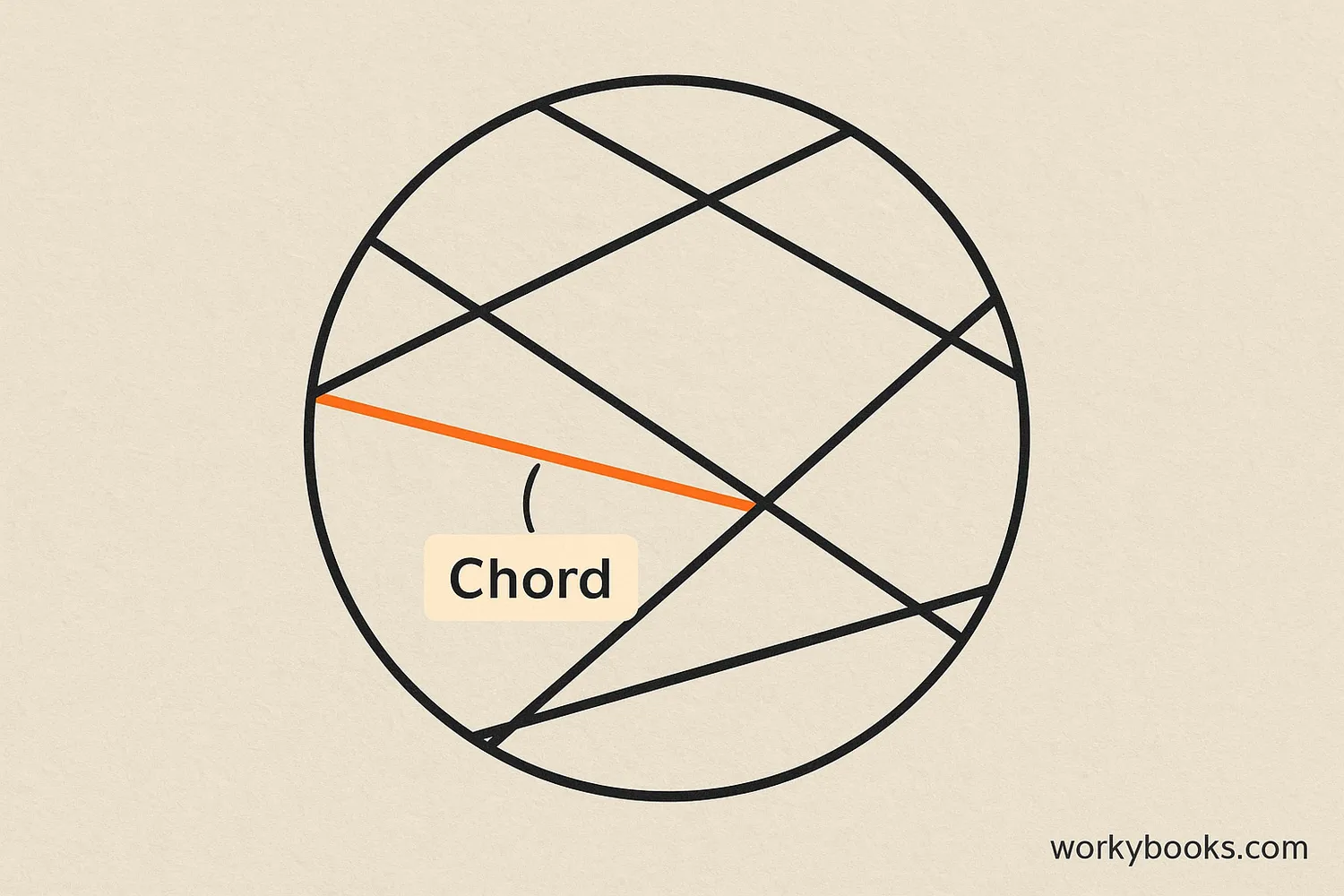
In geometry, a chord is a straight line segment whose both endpoints lie on a circle. Think of it like a straight line that connects two points on a circle's edge.

The longest possible chord in any circle is called the diameter, which passes through the center of the circle. All other chords are shorter than the diameter.

What is a Perpendicular Bisector?

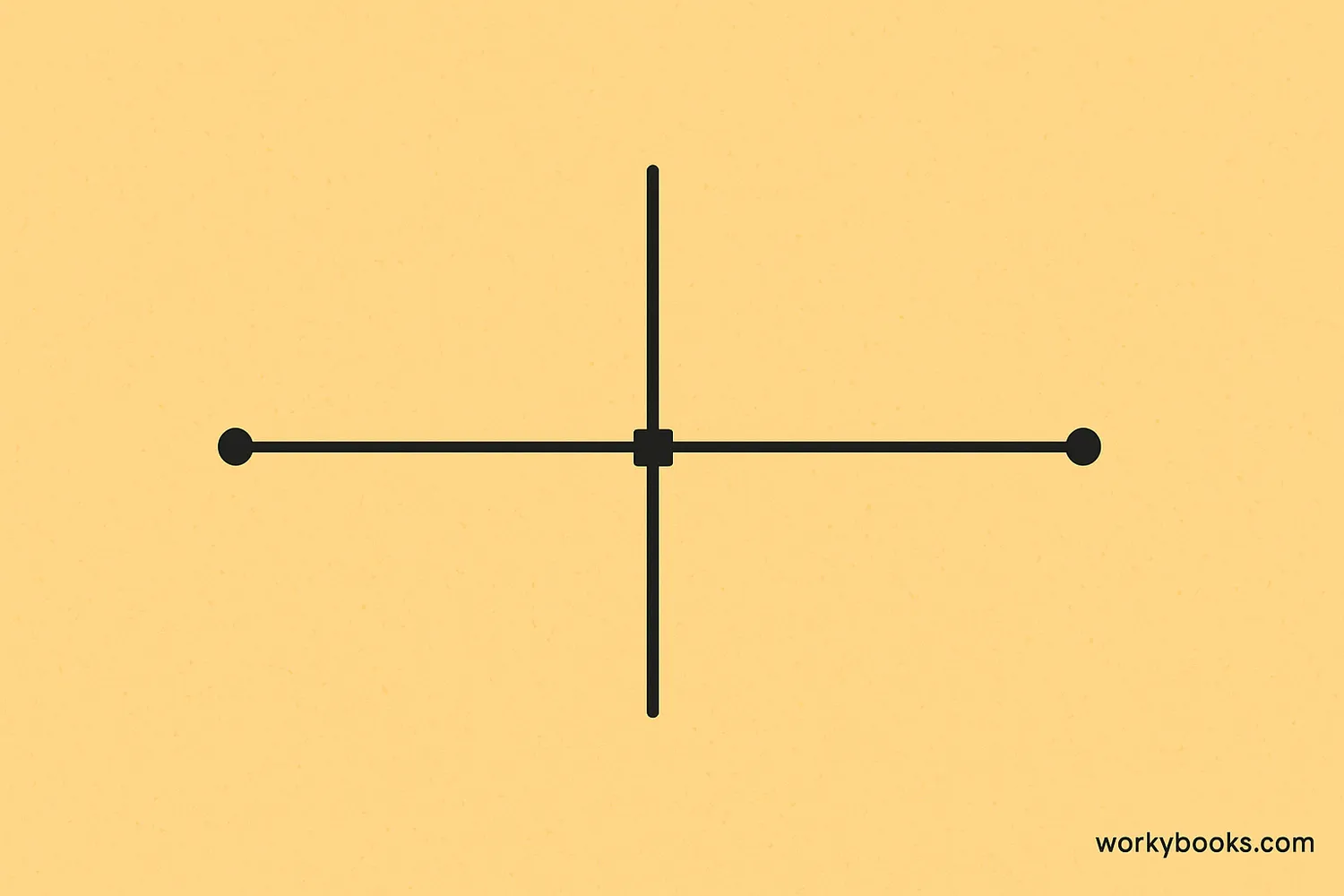
A perpendicular bisector is a line that divides another line into two equal parts at a 90-degree angle. Let's break that down:

Every line segment has exactly one perpendicular bisector. This is a special property that makes perpendicular bisectors very important in geometry.

The Perpendicular Bisector of a Chord Theorem

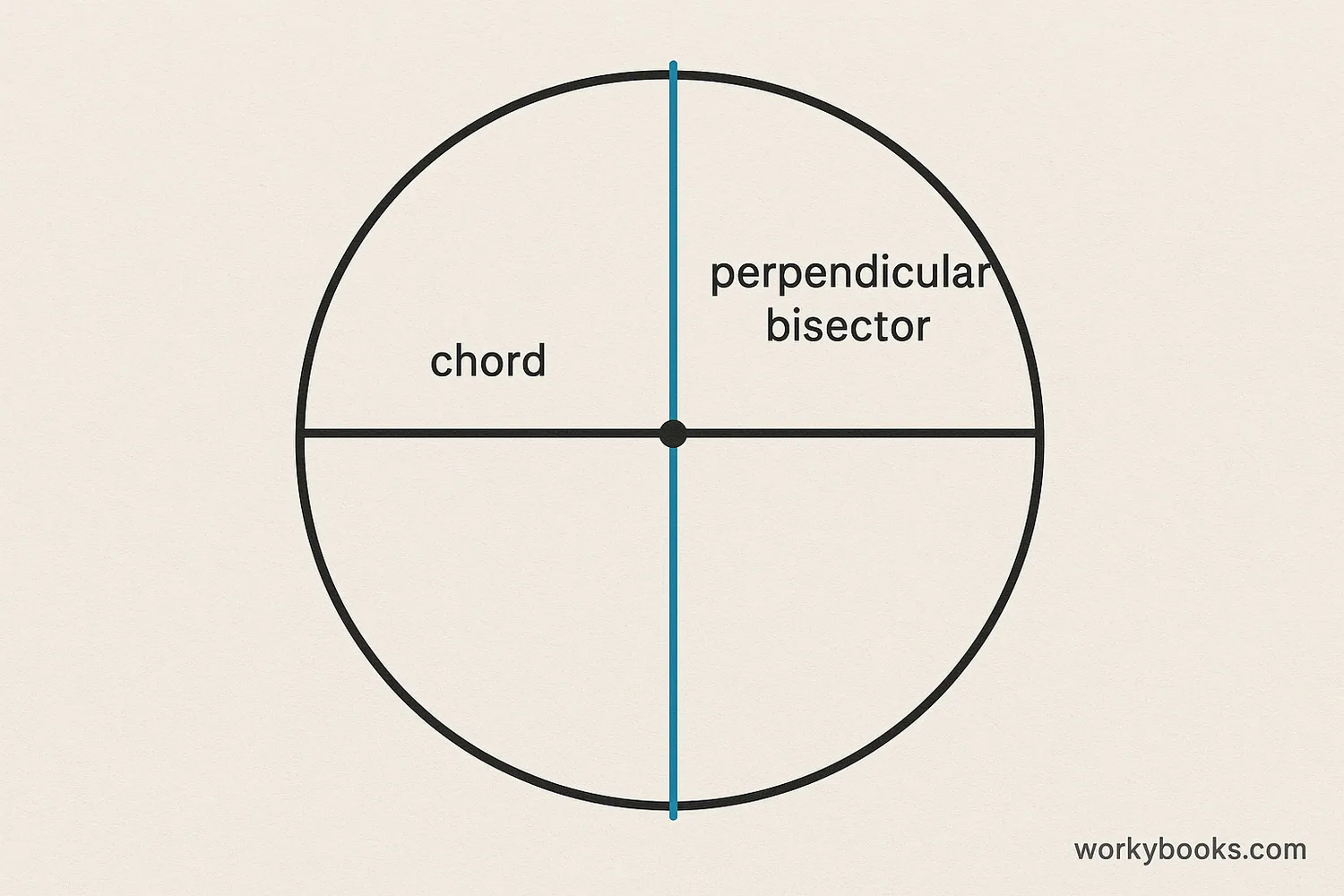
Now for the important theorem! The Perpendicular Bisector of a Chord Theorem states:

This means that if you draw a chord in a circle, and then draw a line that cuts that chord exactly in half at a right angle, that line will always go through the very center of the circle.

This is a special property that only circles have! No other shape has this property for all its chords.

Simple Proof of the Theorem

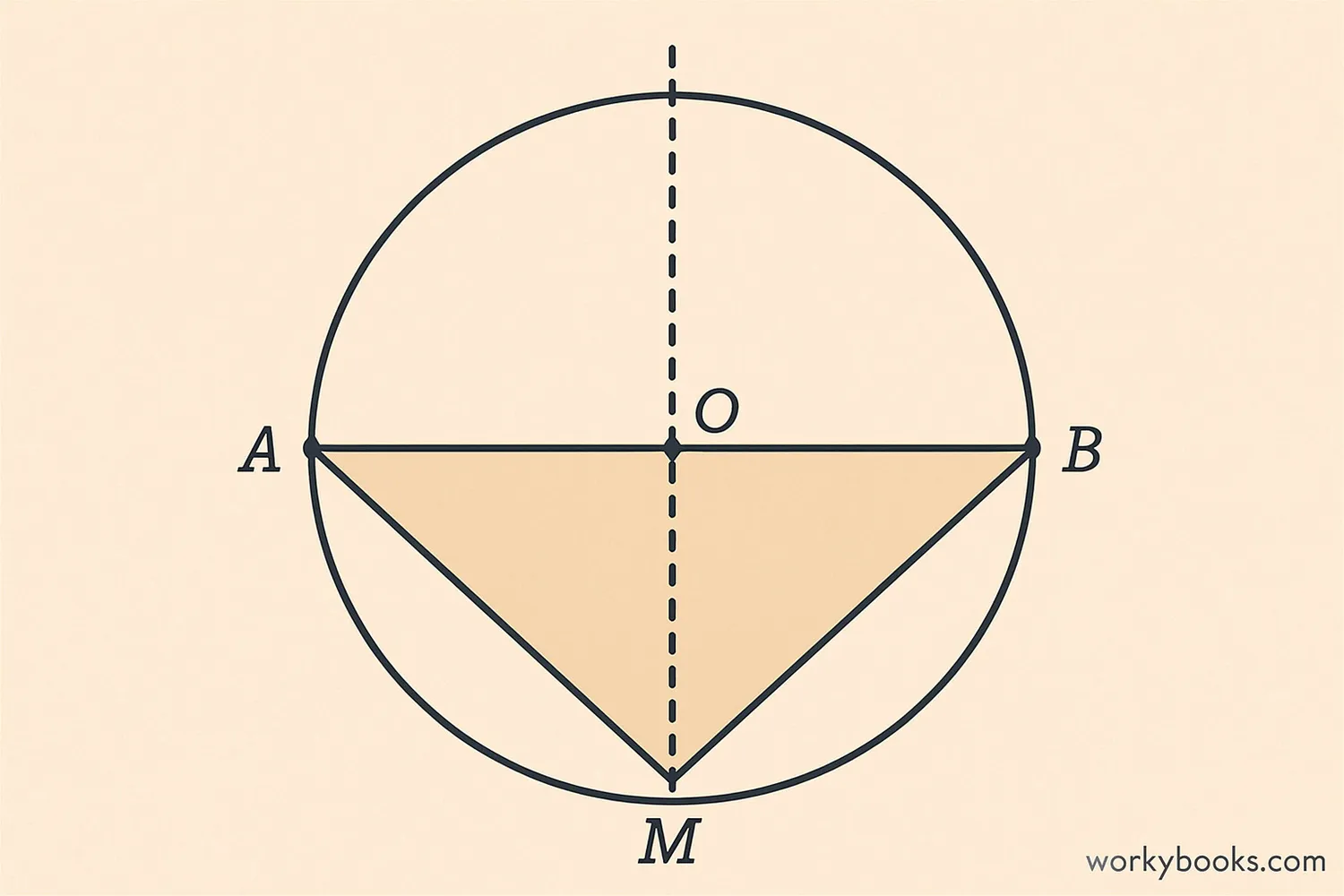
Let's look at a simple way to understand why this theorem is true. We'll use some basic geometry:

This shows that the line from the center to the midpoint of any chord is always perpendicular to that chord. That's the proof!

Examples of the Theorem

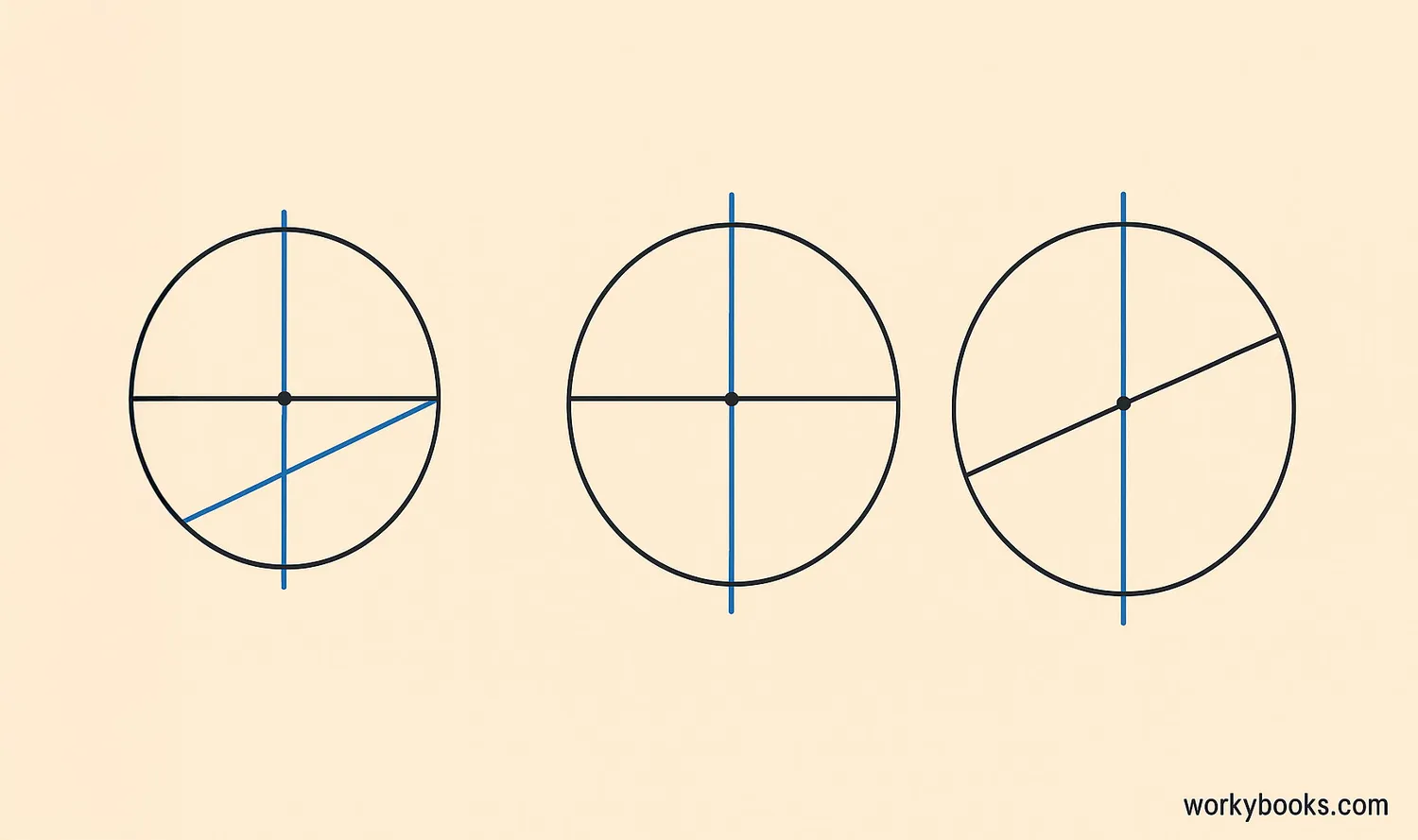
Let's look at some examples to understand how this theorem works in different situations:

This theorem is very useful for solving geometry problems involving circles. Architects and engineers use this principle when designing circular structures!

Geometry Quiz

Test your knowledge with this quiz! Answer all 5 questions to see how much you've learned.

Frequently Asked Questions

Here are answers to some common questions about the perpendicular bisector of a chord:

Math Trivia

Discover some interesting facts about circles and geometry!