Point Slope Form - Definition, Examples, Quiz, FAQ, Trivia
Learn to write equations of lines using a point and slope with easy explanations and practice activities
What is Point Slope Form?
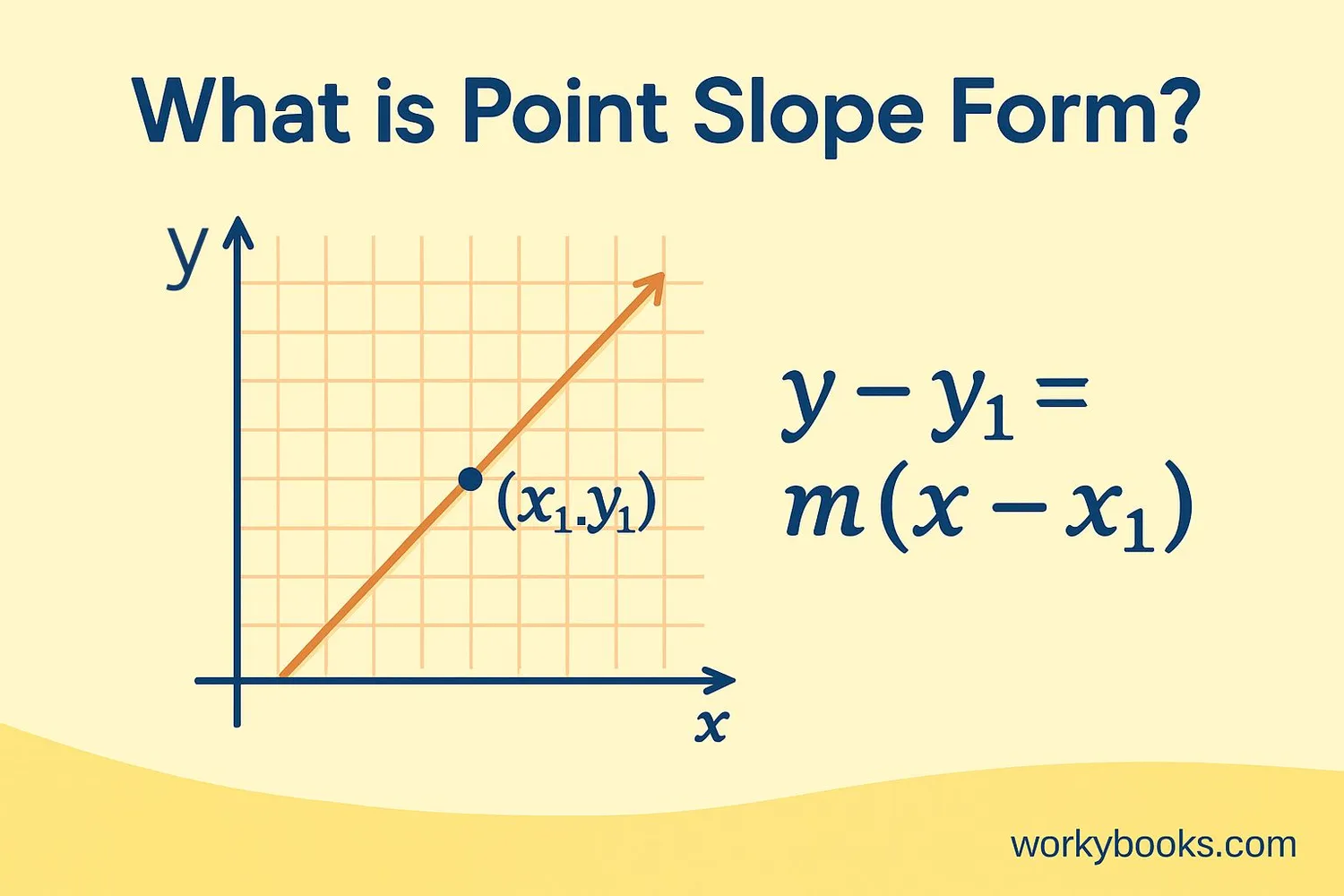
Point slope form is a way to write the equation of a straight line when you know:
1. The slope of the line (m)
2. A point on the line (x₁, y₁)
The formula for point slope form is:
Point Slope Formula
• m is the slope of the line (how steep it is)
• (x₁, y₁) is a specific point on the line
• (x, y) represents any point on the line
This form is especially useful when you know one point and the slope, but not the y-intercept.
Key Concept
The point slope form connects any point on a line to a known point using the slope of the line.
How to Use Point Slope Form

Using point slope form is straightforward when you follow these steps:
Step 1: Identify the slope (m) and a point (x₁, y₁) on the line
Step 2: Plug these values into the point slope formula:
Step 3: Simplify the equation if needed
Let's practice with an example:
Example: Find the equation of a line with slope 3 that passes through point (2, 5)
Step 1: m = 3, (x₁, y₁) = (2, 5)
Step 2: Plug into the formula:
Step 3: Simplify:
So the equation of the line is y = 3x - 1
Remember
Always subtract the coordinates: y - y₁ and x - x₁. This is why it's called point-slope form!
Point Slope Form Examples
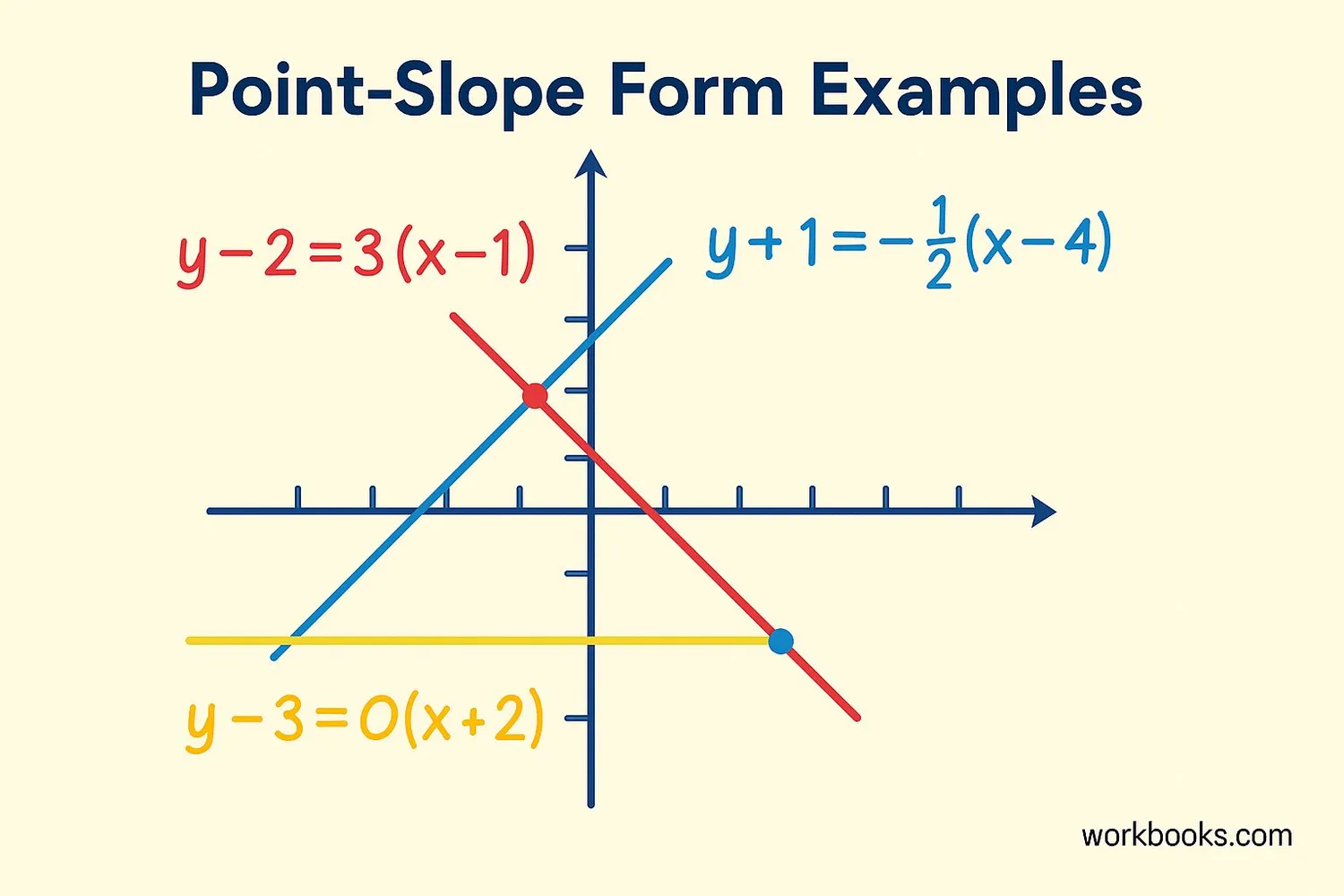
Let's look at more examples to understand how point slope form works:
Write the equation of a line with slope -2 passing through point (1, 4)
Simplify: y - 4 = -2x + 2 → y = -2x + 6
Write the equation of a horizontal line passing through point (3, -2)
Slope of horizontal line is 0
Write the equation of a line passing through points (3, 5) and (6, 11)
First find slope: m = (11 - 5)/(6 - 3) = 6/3 = 2
Use either point, say (3, 5):
Conversion Tip
You can convert between point slope form and other forms like slope-intercept form by simplifying the equation.
Different Forms of Linear Equations

There are three main ways to write the equation of a straight line:
| Form Name | Equation | When to Use |
|---|---|---|
| Point Slope Form | y - y₁ = m(x - x₁) | When you know slope and one point |
| Slope Intercept Form | y = mx + b | When you know slope and y-intercept |
| Standard Form | Ax + By = C | For some calculations and graphing |
Converting between forms:
• From point slope to slope intercept: Simplify and solve for y
• From slope intercept to point slope: Use the y-intercept (0, b) as the point
• From standard form to point slope: Solve for y to find slope, then use any point
Form Tip
Point slope form is often the easiest to use when you have a point and slope but not the y-intercept.
Point Slope Form Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about point slope form:
Math Trivia
Discover interesting facts about linear equations and mathematics:
Ancient Equations
The earliest known linear equations date back to ancient Egypt around 1650 BC! The Rhind Mathematical Papyrus contains problems that we now solve with linear equations.
Real-World Applications
Linear equations are used in everyday life more than you might think! From calculating phone bills to predicting population growth, they help us model relationships between variables.
Space Exploration
NASA uses linear equations to calculate rocket trajectories and satellite orbits. Precise equations ensure spacecraft reach their destinations!
Mathematical Constants
The slope of a line can represent real-world rates like speed (distance over time) or cost (price per item). Understanding slopes helps us understand how things change.





