Quarter Circle - Definition, Examples, Quiz, FAQ, Trivia
Learn about quarter circles with easy explanations, formulas, and practice activities
What is a Quarter Circle?
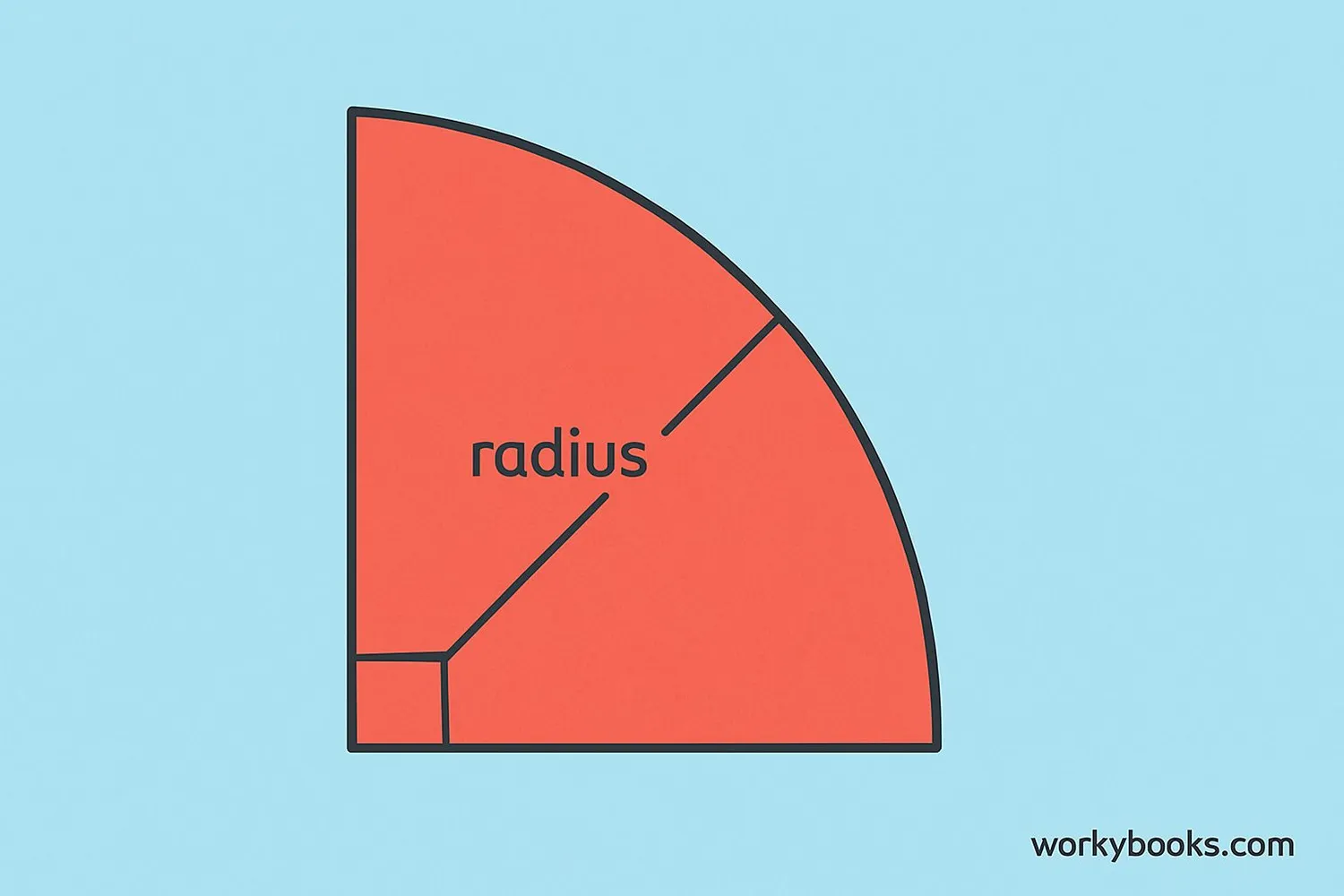
A quarter circle is exactly what it sounds like - one quarter of a full circle. Imagine cutting a pizza into four equal slices. Each slice would be a quarter circle.
Quarter circles are special because they have:
- A curved edge that's one-fourth of the circle's circumference
- Two straight edges (radii) that meet at a right angle (90 degrees)
- An area that's exactly one-fourth of the full circle's area
We see quarter circles in many real-world objects like:
- Pie slices
- Rounded corners of tables or whiteboards
- Some playground equipment
- Architectural designs
Key Concept
A quarter circle is a 90-degree sector of a circle, bounded by two radii and a circular arc.
Quarter Circle Properties
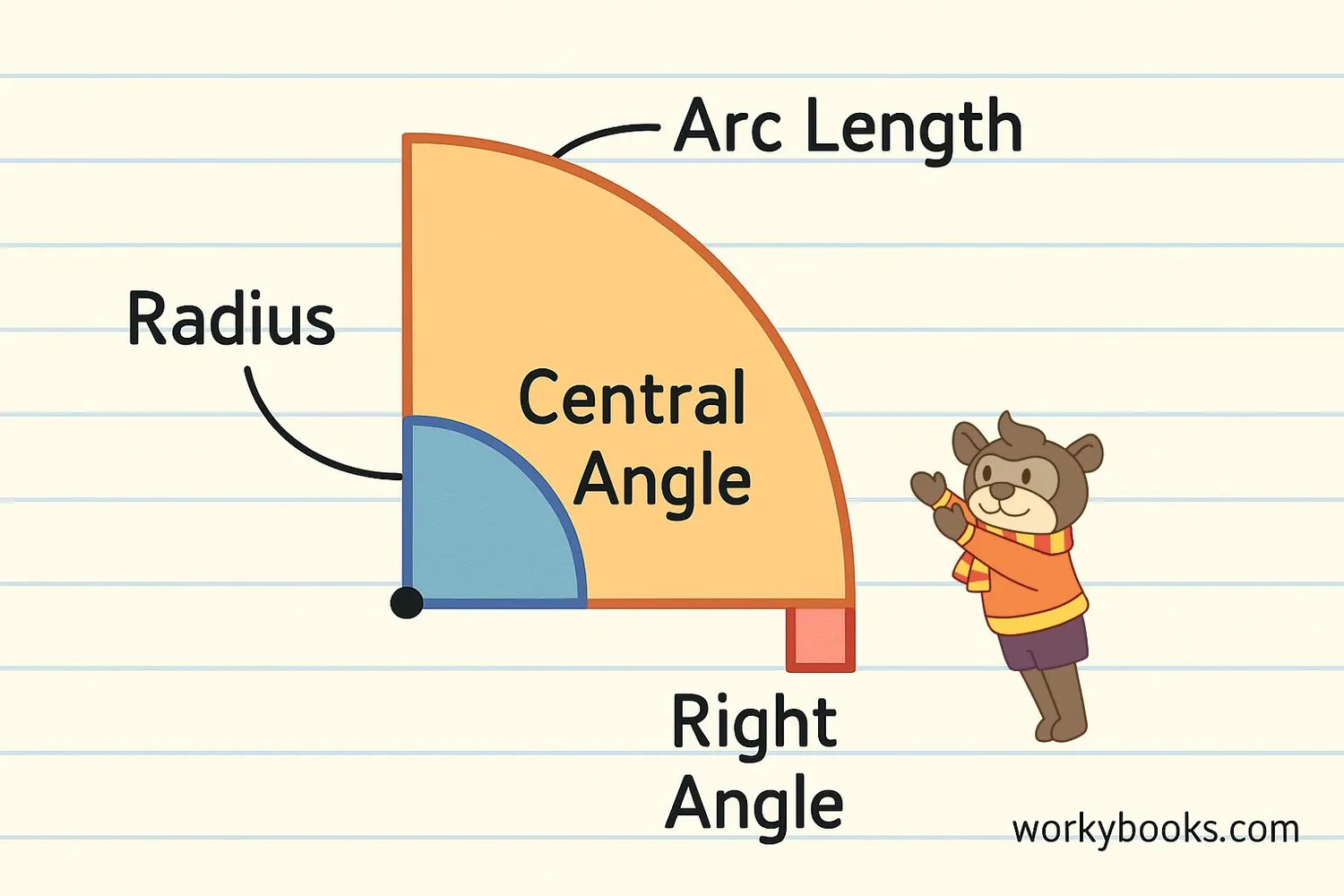
Let's look at the important properties of a quarter circle:
1. Radius (r): The distance from the center to any point on the curved edge. Both straight sides are radii.
2. Central Angle: The angle between the two radii is always 90 degrees (a right angle).
3. Arc Length: The curved part is exactly one-fourth of the circle's full circumference.
4. Perimeter: The total distance around includes the arc plus both radii.
5. Area: The space inside is one-fourth of the full circle's area.
These properties help us calculate measurements and solve problems involving quarter circles.
Remember
In a quarter circle, the two radii always form a right angle (90 degrees) at the center.
Quarter Circle Formulas

Here are the important formulas for working with quarter circles (where r is the radius):
Area Formula
This is one-fourth of the full circle's area.
Perimeter Formula
Includes the curved arc plus both straight radii.
Arc Length Formula
This is one-fourth of the full circumference.
Example: For a quarter circle with radius 4 cm:
Area = ¼ × π × 4² ≈ 12.57 cm²
Perimeter = (π × 4)/2 + 8 ≈ 14.28 cm
Arc Length = (π × 4)/2 ≈ 6.28 cm
Real-World Examples

Let's solve some real-world problems using quarter circles:
Example 1: A pizza has a diameter of 12 inches. What is the area of one slice (quarter circle)?
Solution: Radius = 6 inches. Area = ¼ × π × 6² ≈ 28.27 in²
Example 2: A garden has a quarter-circle flower bed with radius 3 feet. What length of edging is needed?
Solution: Perimeter = (π × 3)/2 + 6 ≈ 10.71 feet
Example 3: A table has rounded corners that are quarter circles with radius 2 inches. What's the total area of all four rounded corners?
Solution: Area of one corner = ¼ × π × 2² ≈ 3.14 in². Total area ≈ 12.57 in²
Look around you - can you find any quarter circle shapes in your classroom or home?
Practice Tip
Remember to always identify the radius first when solving quarter circle problems.
Quarter Circle Quiz
Test your knowledge with this 5-question quiz about quarter circles:
Frequently Asked Questions
Here are answers to common questions about quarter circles:
Geometry Trivia
Discover interesting facts about circles and geometry:
Ancient Circles
The ancient Greeks were fascinated by circles. They discovered many circle properties using only compass and straightedge constructions over 2000 years ago.
Perfect Circles
In nature, perfect circles are rare. Even the Sun and Moon appear as perfect circles but are actually slightly elliptical. The most perfect natural circles may be soap bubbles.
π in Space
NASA uses π (pi) to calculate trajectories of spacecraft. The Mars rover landing required π calculations accurate to 15 decimal places for precision landing.
Circle Records
The world's largest circular building is the Singapore Flyer observation wheel, with a diameter of 150 meters (492 feet). That's a circumference of about 471 meters!





