Reciprocals - Definition, Examples, Quiz, FAQ, Trivia
Learn how to find and use reciprocals with easy explanations, visual examples, and practice activities
What is a Reciprocal?
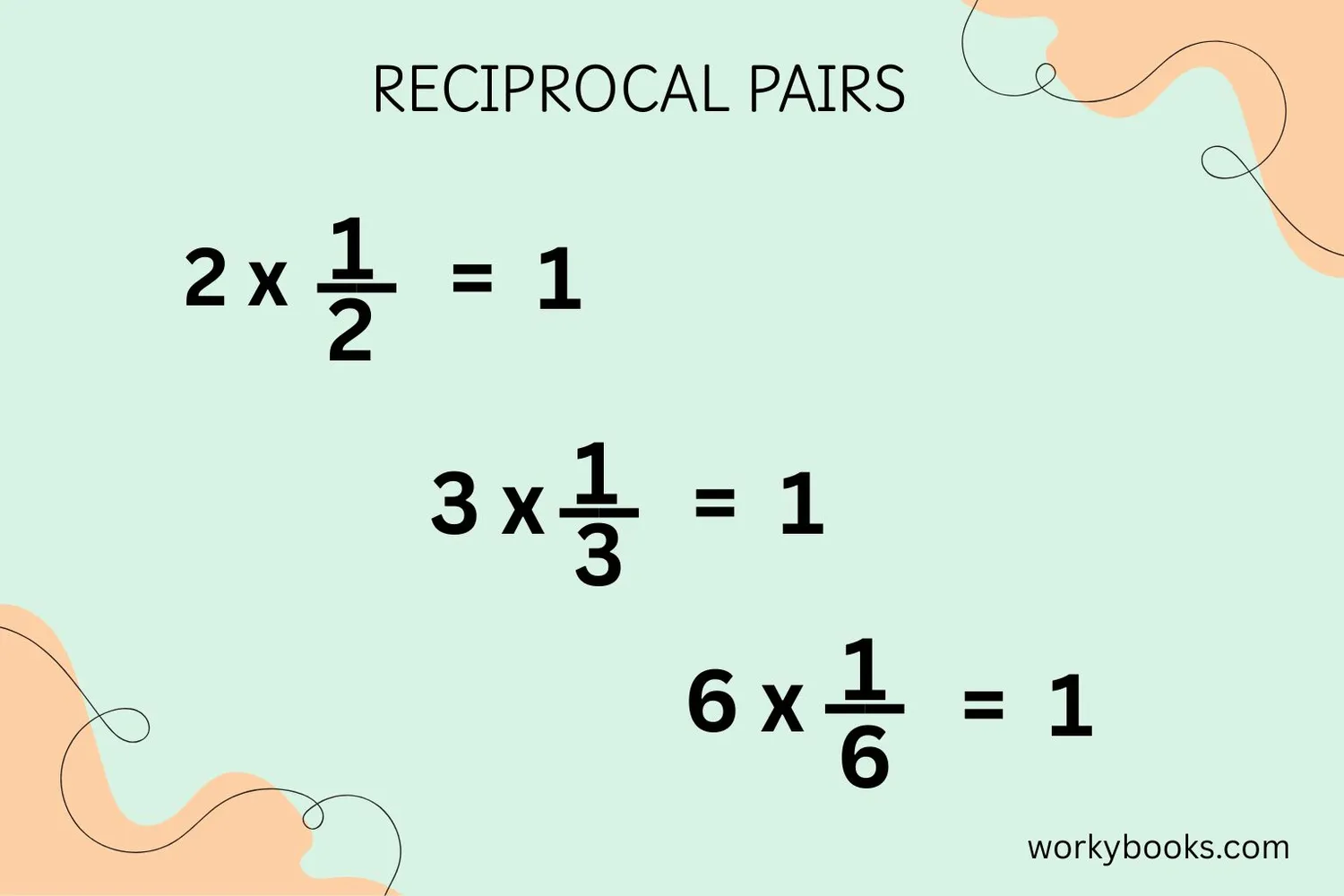
A reciprocal is a special number that when multiplied by the original number, gives you 1. It's also called the multiplicative inverse because it "undoes" the multiplication.
The reciprocal of a number is simply 1 divided by that number. For any number "a" (except zero), the reciprocal is 1/a.
Why is this important? Reciprocals help us solve equations, divide fractions, and understand inverse relationships in math and science. When you multiply a number by its reciprocal, you always get 1!
Reciprocal Definition
The reciprocal of a number is 1 divided by that number
Key Property
Any number multiplied by its reciprocal equals 1. This is true for whole numbers, fractions, and decimals (except zero).
How to Find the Reciprocal
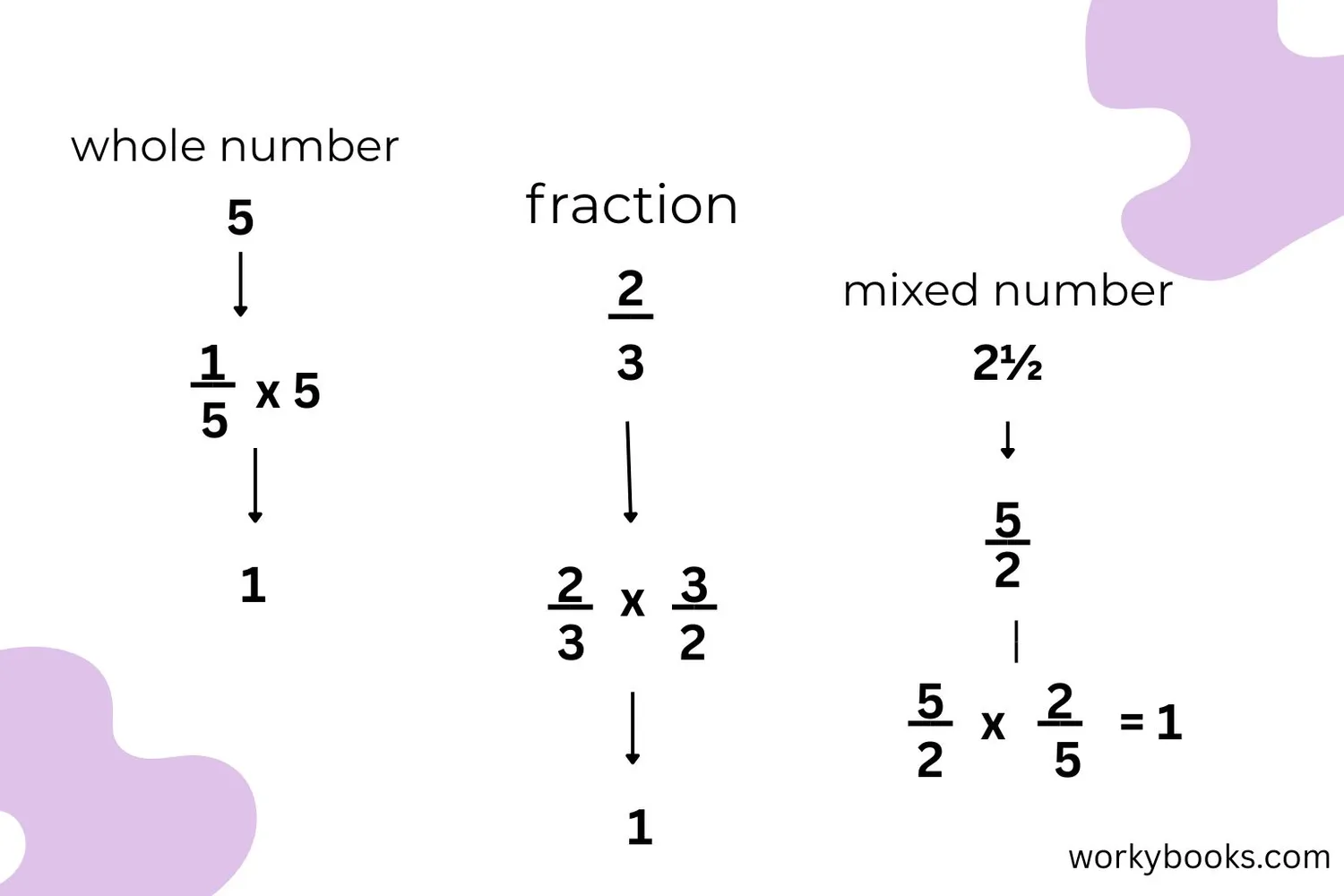
Finding the reciprocal is simple once you know these steps:
For Whole Numbers
Original Number
Write the number as a fraction: 5/1
Flip the Fraction
Swap numerator and denominator
Check
Multiplication gives 1
For Fractions
Original Fraction
Numerator: 3, Denominator: 4
Flip the Fraction
Swap numerator and denominator
Check
Multiplication gives 1
For Mixed Numbers
Original Number
Convert to improper fraction: 5/2
Flip the Fraction
Swap numerator and denominator
Check
Multiplication gives 1
Important Note
The reciprocal of zero (0) is undefined because you cannot divide by zero. There's no number that can multiply by 0 to give 1.
Reciprocal of Fractions
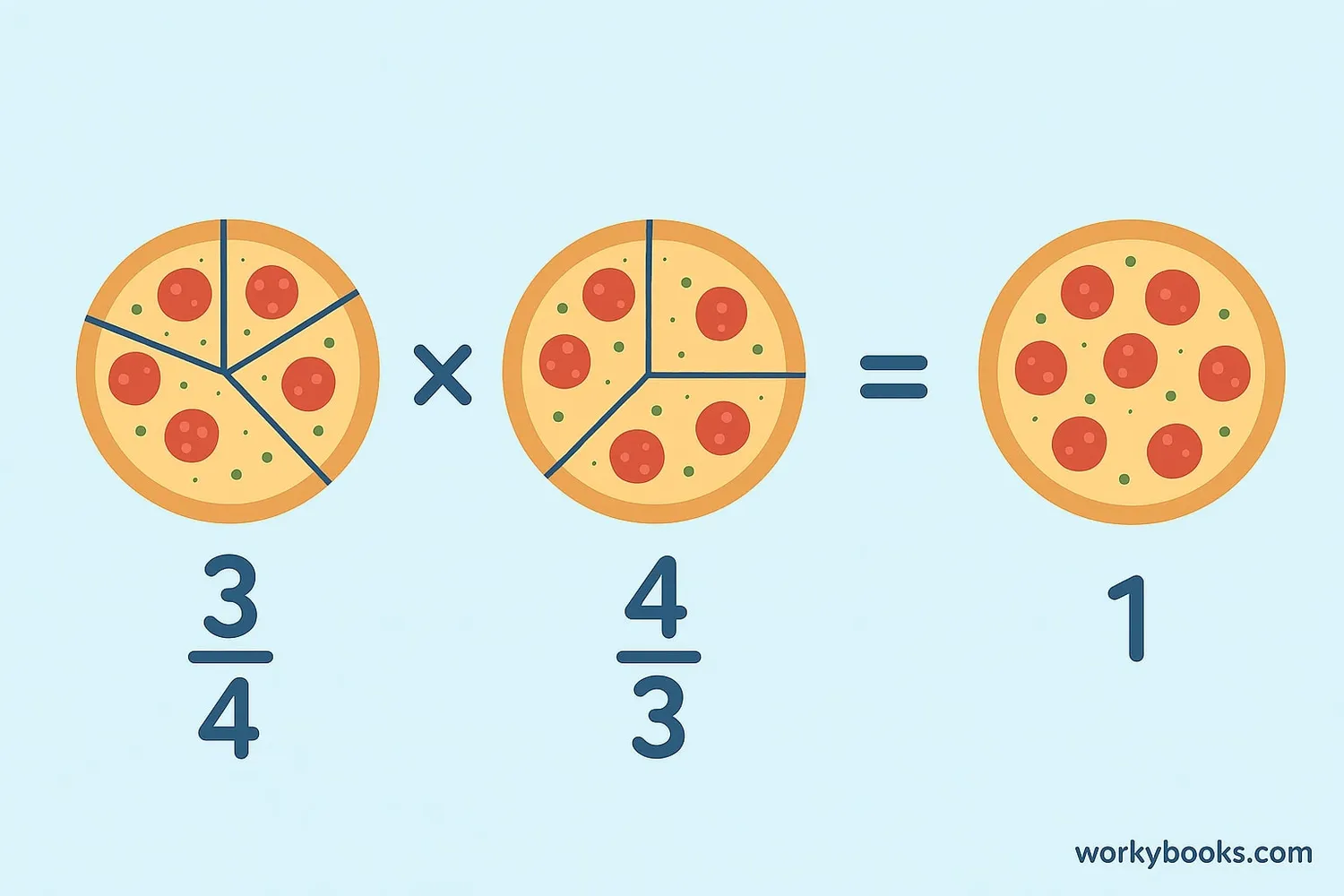
Fractions have a special relationship with reciprocals. The reciprocal of a fraction is simply the fraction flipped upside down!
For any fraction a/b (where a and b are not zero), the reciprocal is b/a. This works because:
Fraction Reciprocal Formula
Multiplying a fraction by its reciprocal always gives 1
Dividing Fractions
Problem
Solution
Multiply by reciprocal of ⅓
Check
Verifies our answer
Special Cases
The reciprocal of 1 is 1 (since 1 × 1 = 1). The reciprocal of a unit fraction (like 1/5) is a whole number (5).
Reciprocal Examples

Let's look at some examples of finding reciprocals:
| Number | Reciprocal | Check (Number × Reciprocal = 1) |
|---|---|---|
| 8 | 1/8 | 8 × 1/8 = 8/8 = 1 |
| 1/2 | 2/1 = 2 | 1/2 × 2/1 = 2/2 = 1 |
| 3/5 | 5/3 | 3/5 × 5/3 = 15/15 = 1 |
| 0.2 (1/5) | 5 | 0.2 × 5 = 1 |
| 1¼ (5/4) | 4/5 | 5/4 × 4/5 = 20/20 = 1 |
| 10 | 0.1 (1/10) | 10 × 0.1 = 1 |
Practice Problem
Problem
Solution
Check
Remember
The reciprocal of a reciprocal brings you back to the original number: 1/(1/a) = a
Reciprocal Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about reciprocals:
Math Trivia
Discover interesting facts about reciprocals and mathematics:
Ancient Origins
The concept of reciprocals dates back to ancient Egypt around 1800 BC. Egyptians used unit fraction reciprocals (like 1/2, 1/3, 1/4) in their mathematical calculations and problem-solving.
Physics Connection
In physics, many relationships are reciprocal. For example, speed and time are reciprocals when distance is constant: doubling your speed halves the time needed to cover a fixed distance.
Musical Harmonies
In music, reciprocals create harmonies. When one string is half the length of another, it vibrates at twice the frequency, creating the musical interval of an octave - a perfect reciprocal relationship.
Golden Ratio
The famous Golden Ratio (approximately 1.618) has a reciprocal that is exactly one less than itself: 1/1.618 ≈ 0.618. This unique property makes it appear in nature, art, and architecture.





