Relations in Math - Definition, Examples, Quiz, FAQ, Trivia
Learn about connections between numbers with easy explanations, examples, and interactive activities
What is a Mathematical Relation?
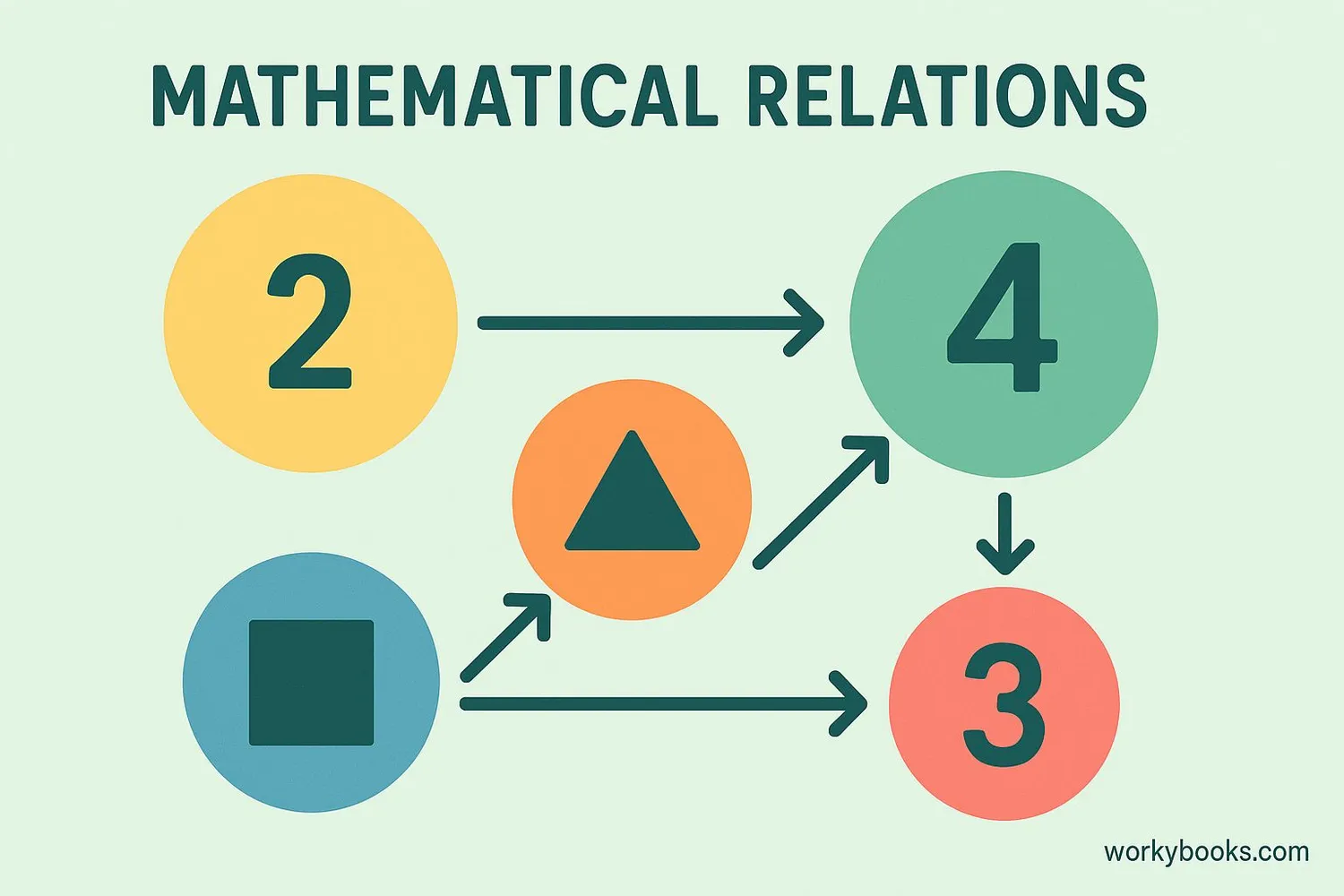
In mathematics, a relation describes a connection or relationship between different elements. Think of it like a friendship between numbers or objects!
For example, we can have a relation that connects:
- Students to their favorite subjects
- Numbers to their squares (2 → 4, 3 → 9)
- Shapes to the number of sides they have
A relation is made up of ordered pairs (like (x, y)) that show which elements are connected. The set of all first elements is called the domain, and the set of all second elements is the range.
Example: Fruit Colors
{(Apple, Red), (Banana, Yellow), (Grape, Purple)}
Domain: {Apple, Banana, Grape}
Range: {Red, Yellow, Purple}
Key Concept
A relation is a set of ordered pairs showing connections between elements from two different sets.
Representing Relations
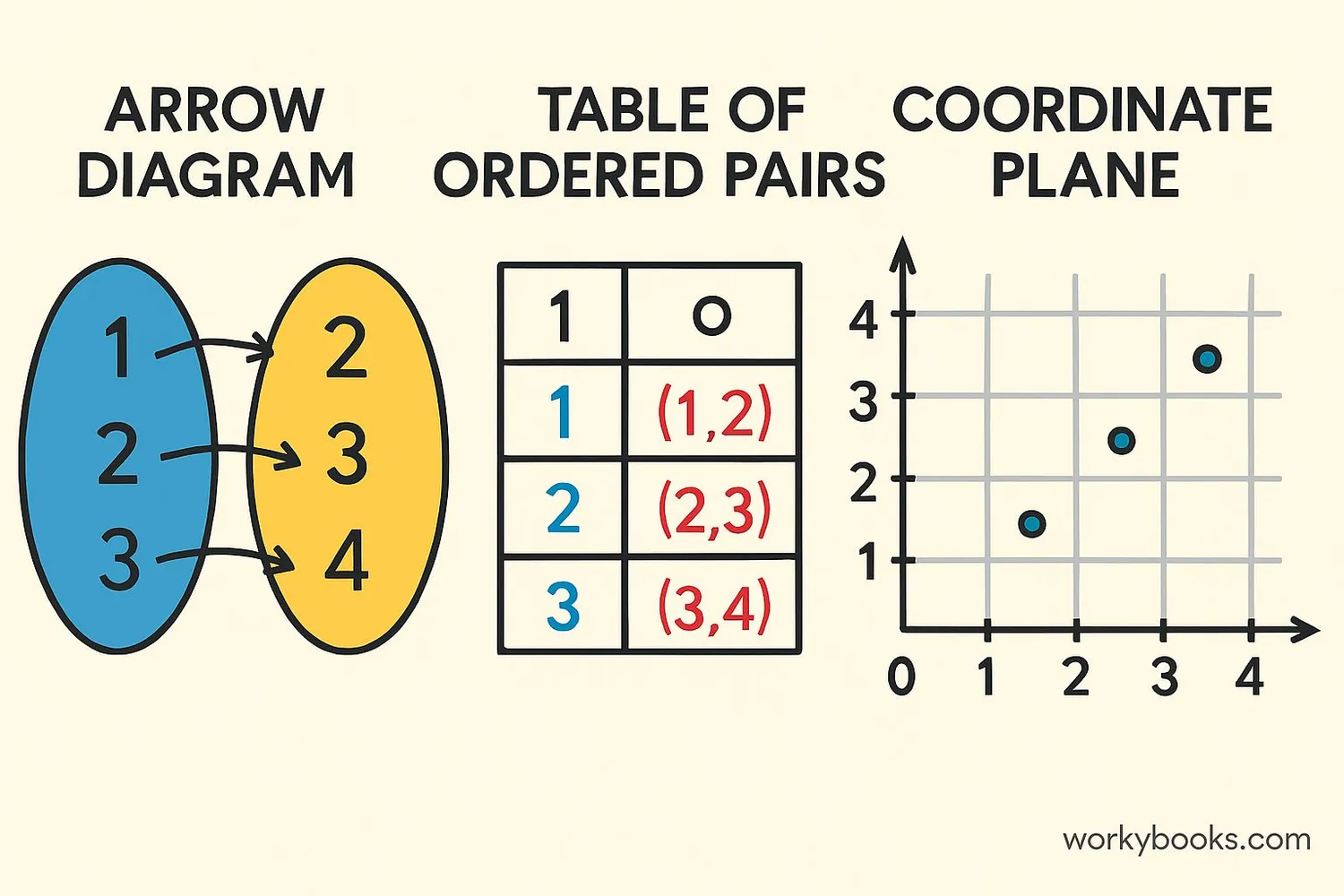
We can show relations in several different ways:
1. Arrow Diagrams: Draw elements from one set connected to elements in another set with arrows.
2. Tables: List the ordered pairs in rows.
3. Graphs: Plot the ordered pairs on a coordinate plane.
4. Mapping Diagrams: Show connections between domain and range elements.
Example: Number Relations
Relation: "is half of"
{(2,4), (3,6), (4,8)}
Domain: {2,3,4}
Range: {4,6,8}
Remember
Each representation shows the same relationships in different ways. Choose the one that helps you understand best!
Types of Relations
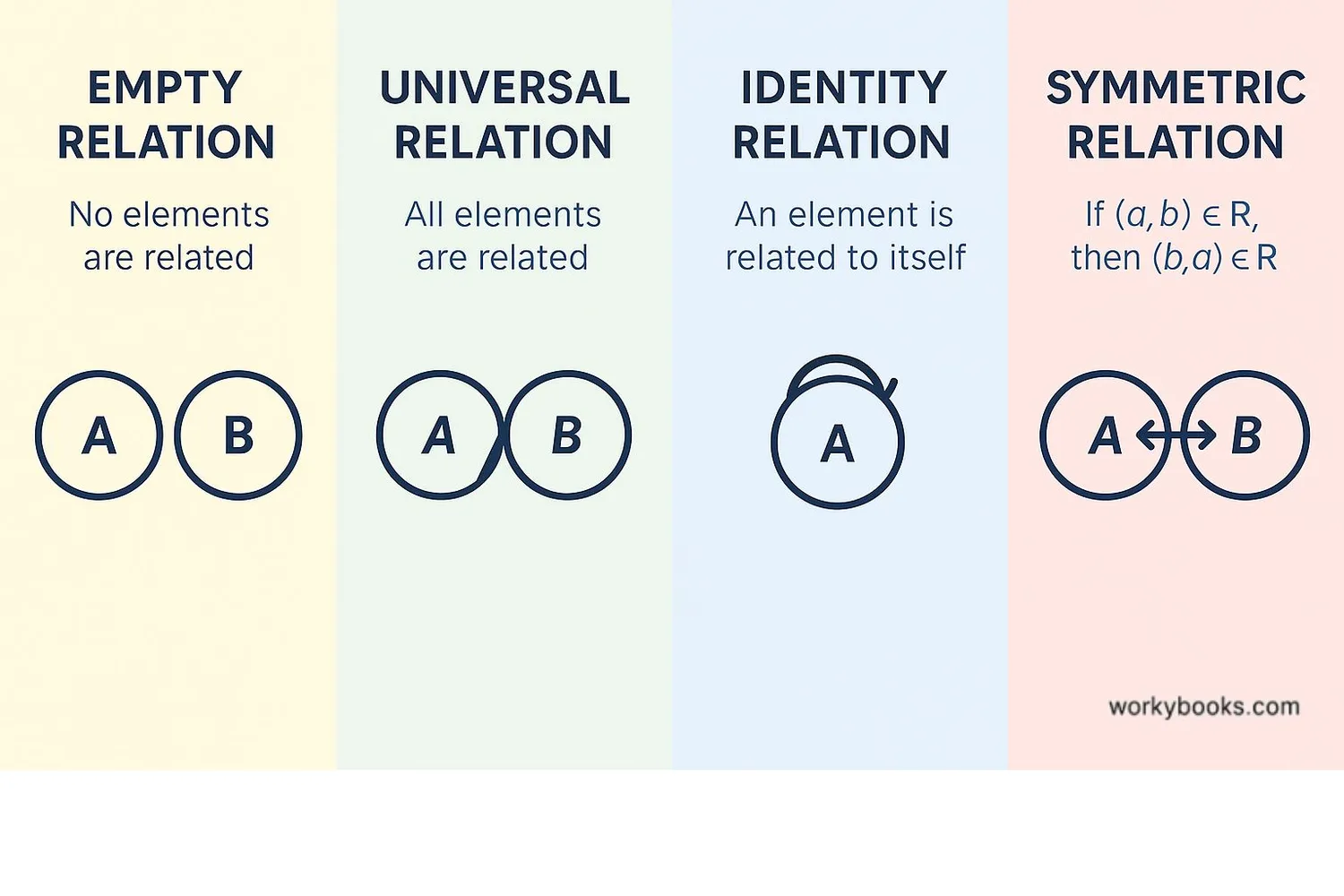
There are several special types of relations in mathematics:
Empty Relation: When there are no connections between sets. Like a classroom where no one has a birthday in December.
Universal Relation: When every element in set A is related to every element in set B. Like all students being friends with the teacher.
Identity Relation: When each element is only related to itself. Like students having the same name as themselves.
Symmetric Relation: If A is related to B, then B is also related to A. Like sibling relationships (if Anna is sister to Ben, then Ben is brother to Anna).
| Relation Type | Description | Example |
|---|---|---|
| Empty | No elements are related | Students and empty lockers |
| Universal | All elements are related | All students in the same school |
| Identity | Element related to itself | Numbers equal to themselves |
| Symmetric | If A→B then B→A | Sibling relationships |
Relation Tip
Think about real-world relationships to understand different types of mathematical relations!
Functions vs Relations
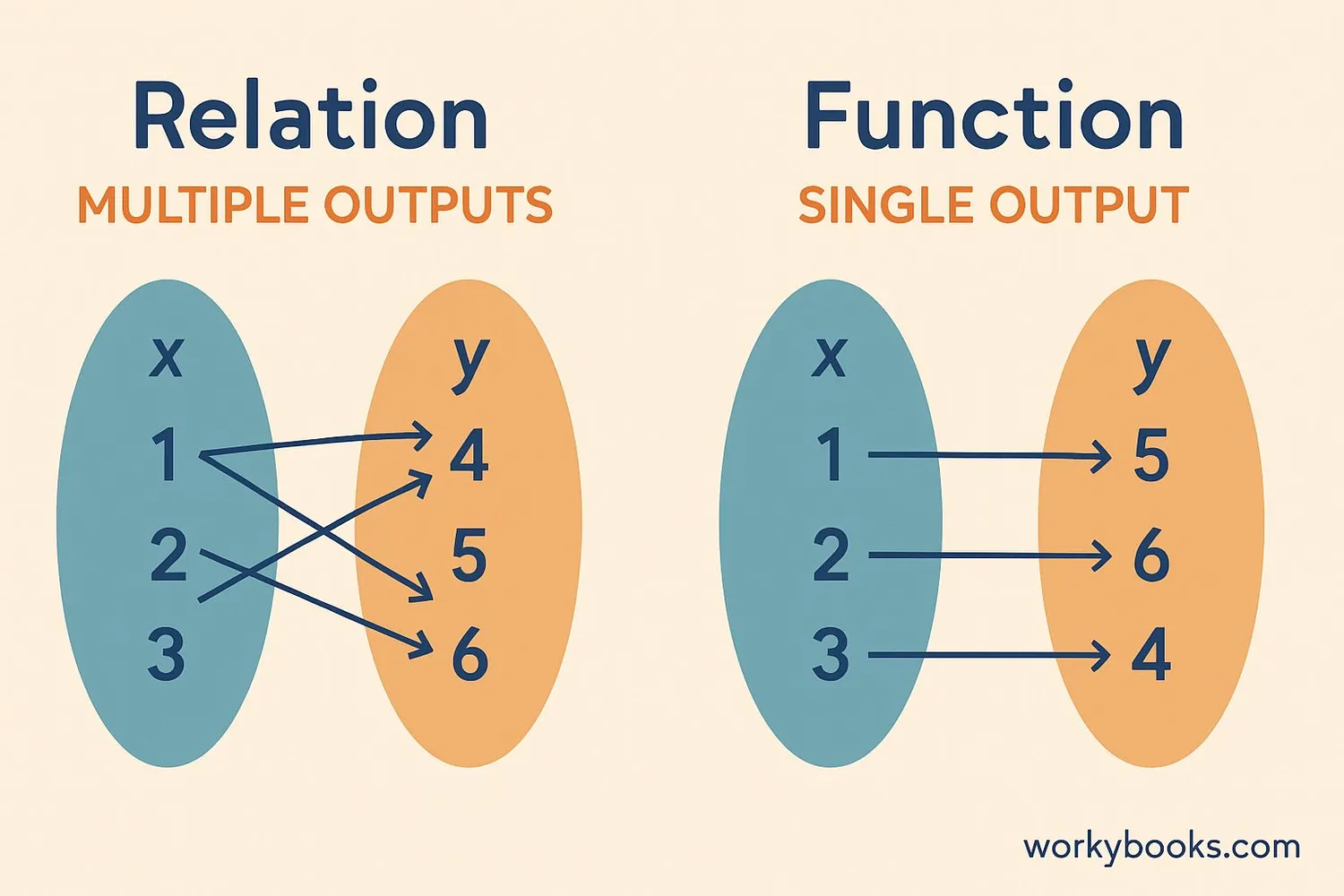
All functions are relations, but not all relations are functions! What makes functions special?
A function is a special type of relation where:
- Each input has exactly one output
- No input has multiple outputs
Example of a Function: Student ID numbers → Students (each ID has only one student)
Example of Relation (Not Function): Students → Favorite colors (a student might like multiple colors)
Function Test
If you can draw a vertical line that passes through more than one point on the graph, it's not a function!
Remember
Functions are like machines: you put one thing in, and get exactly one thing out!
Relations Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about relations in math:
Math Relations Trivia
Discover interesting facts about mathematical relations:
Ancient Relations
The concept of mathematical relations dates back to ancient Greece, where mathematicians like Euclid studied relationships between geometric shapes and numbers.
Brain Connections
Your brain naturally understands relations! When you recognize that dogs and cats are both pets, you're forming a mathematical relation in your mind.
Infinite Relations
Some relations can be infinite! For example, the relation "is greater than" for numbers goes on forever in both directions.
Worldwide Web
The entire internet can be thought of as a giant mathematical relation, with websites connected by links between them.





