System of Equations - Definition, Examples, Quiz, FAQ, Trivia
Learn to solve equations with two variables using visual examples and step-by-step methods
What is a System of Equations?
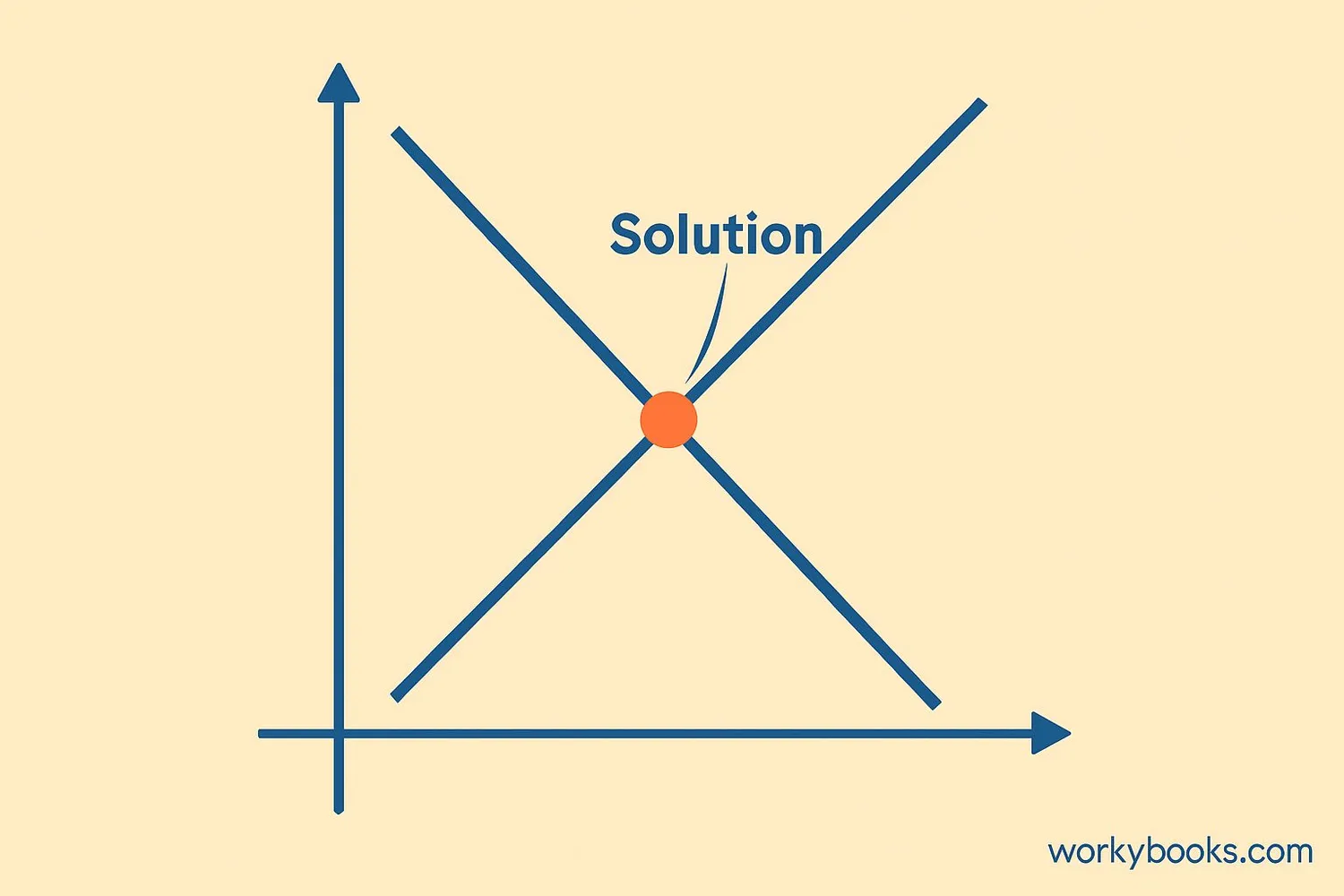
A system of equations is a set of two or more equations with the same variables. We solve the system to find the values of the variables that make all equations true at the same time.
Think of it like solving a puzzle where you have two clues. For example:
Clue 1: x + y = 10
Clue 2: x - y = 2
The solution to this system is x = 6 and y = 4, because 6 + 4 = 10 and 6 - 4 = 2. Both equations are satisfied with these values.
Key Concept
A solution to a system of equations makes all equations true at the same time.
Solving Methods
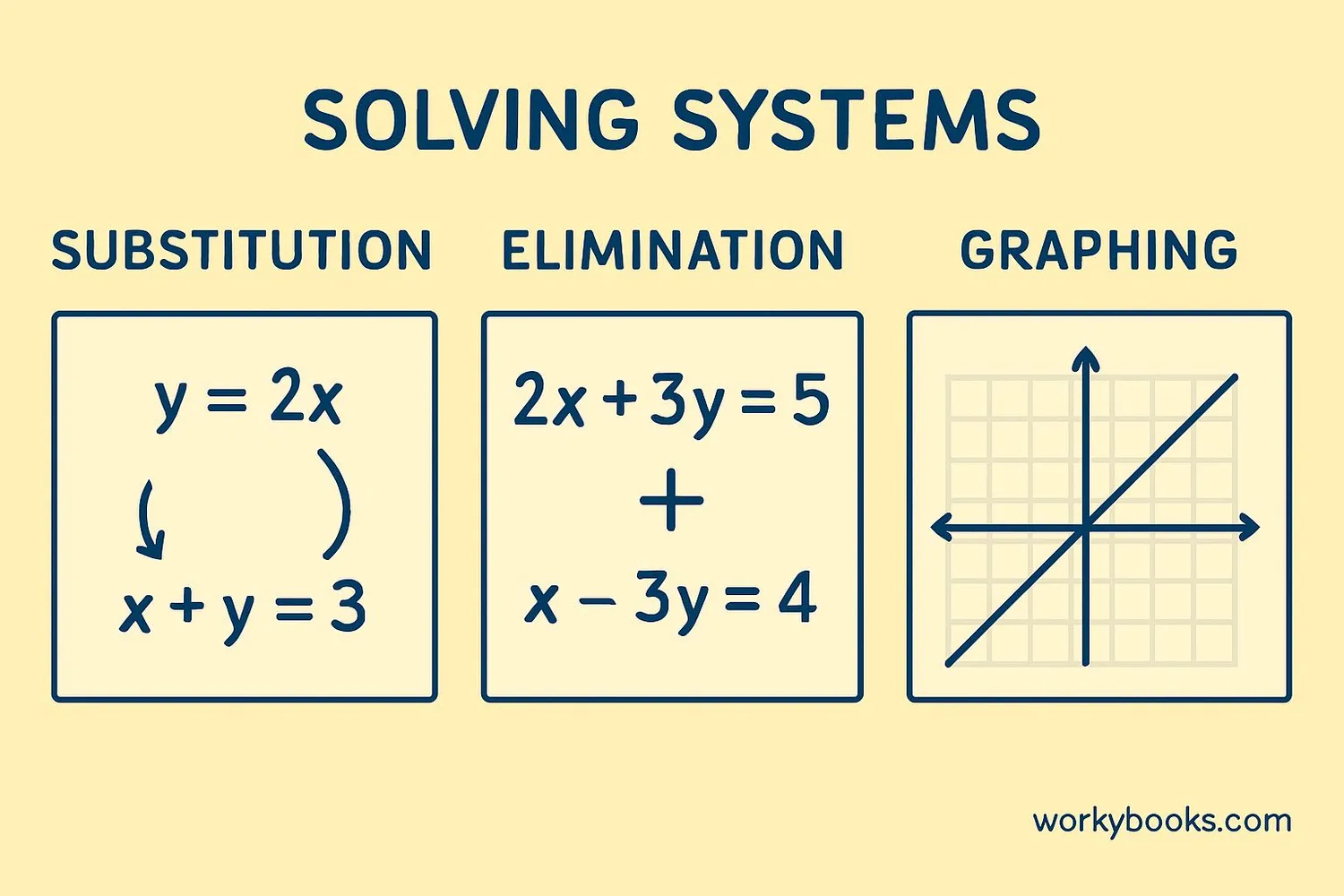
There are several ways to solve systems of equations. Let's explore the three main methods:
Substitution Method
This method works by solving one equation for one variable and substituting that expression into the other equation.
- Solve one equation for one variable
- Substitute that expression into the other equation
- Solve for the remaining variable
- Substitute back to find the first variable
Solve:
Equation 1: y = 2x + 1
Equation 2: 3x + y = 9
Substitute y from Equation 1 into Equation 2:
3x + (2x + 1) = 9
5x + 1 = 9
5x = 8
x = 1.6
Then y = 2(1.6) + 1 = 4.2
Elimination Method
This method adds or subtracts equations to eliminate one variable, making it easier to solve for the other.
- Make coefficients of one variable opposites
- Add the equations together
- Solve for the remaining variable
- Substitute to find the other variable
Solve:
Equation 1: 2x + 3y = 7
Equation 2: 4x - 3y = 5
Add both equations:
(2x + 3y) + (4x - 3y) = 7 + 5
6x = 12
x = 2
Then 2(2) + 3y = 7 → 4 + 3y = 7 → 3y = 3 → y = 1
Graphing Method
This method involves graphing both equations and finding their point of intersection.
- Graph both equations on the same coordinate plane
- Find the point where the lines intersect
- The intersection point is the solution (x, y)
Solve by graphing:
y = 2x + 1
y = -x + 7
Graph both lines. They intersect at (2, 5), so the solution is x=2, y=5.
Types of Systems
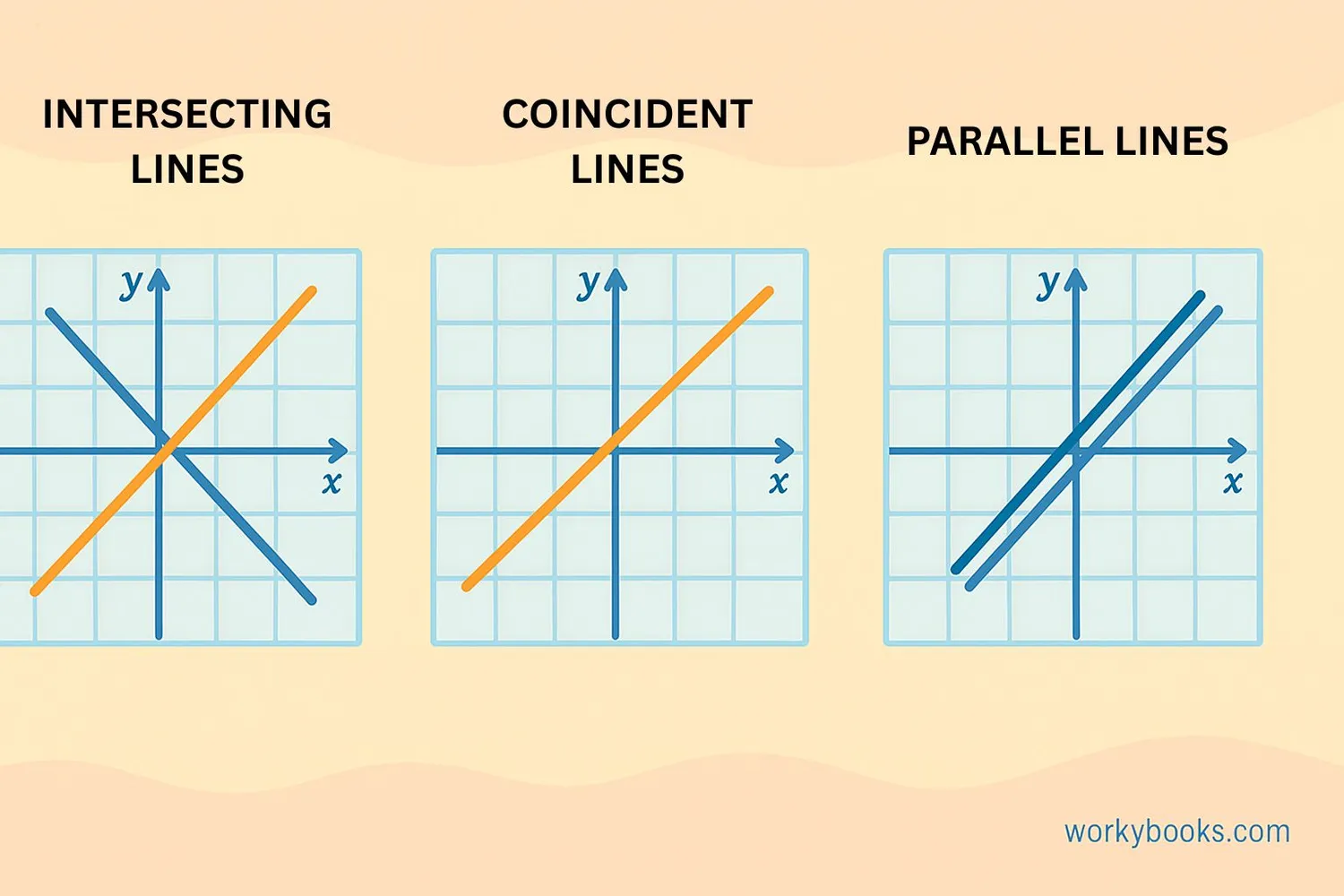
Systems of equations can have different types of solutions:
Consistent and Independent
This system has exactly one solution. The lines intersect at one point.
- Different slopes
- One solution
- Example: x + y = 5, x - y = 1
Inconsistent
This system has no solution. The lines are parallel and never intersect.
- Same slope, different y-intercepts
- No solution
- Example: y = 2x + 3, y = 2x - 1
Consistent and Dependent
This system has infinitely many solutions. The lines are identical.
- Same slope and same y-intercept
- Infinite solutions
- Example: 2x + 4y = 8, x + 2y = 4
Remember
Two lines can either intersect once (one solution), never intersect (no solution), or always intersect (infinite solutions).
Real-World Examples

Systems of equations help solve real-world problems. Here are some examples:
At the school fair, Sarah sold juice for $2 per cup and cookies for $1 each. She sold 30 items total and made $45. How many cups of juice and cookies did she sell?
Solution:
Let j = number of juice cups, c = number of cookies
Equation 1: j + c = 30 (total items)
Equation 2: 2j + c = 45 (total money)
Subtract Equation 1 from Equation 2: (2j + c) - (j + c) = 45 - 30
j = 15
Then 15 + c = 30 → c = 15
Sarah sold 15 juice cups and 15 cookies.
A school has buses and vans for a field trip. Each bus holds 40 students, each van holds 10 students. There are 10 vehicles total that can carry 220 students. How many buses and vans are there?
Solution:
Let b = number of buses, v = number of vans
Equation 1: b + v = 10 (total vehicles)
Equation 2: 40b + 10v = 220 (total students)
Multiply Equation 1 by 10: 10b + 10v = 100
Subtract from Equation 2: (40b + 10v) - (10b + 10v) = 220 - 100
30b = 120 → b = 4
Then 4 + v = 10 → v = 6
There are 4 buses and 6 vans.
Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about systems of equations:
Math Trivia
Discover interesting facts about equations and mathematics:
Ancient Algebra
The earliest known systems of equations solutions date back to ancient Babylon around 1800 BC. Babylonian mathematicians solved systems with up to five equations!
Real-World Applications
Systems of equations are used in engineering to design bridges, in economics to model markets, in computer graphics for animation, and even in GPS technology to calculate your position!
Space Exploration
NASA uses systems of equations to calculate rocket trajectories. When sending spacecraft to other planets, they solve systems with thousands of equations to plot the perfect course!
Large Systems
The largest system of equations ever solved had over 2 million variables! Scientists used supercomputers to solve complex problems in weather prediction and molecular modeling.





