Trigonometry - Definition, Examples, Quiz, FAQ, Trivia
Discover the world of triangles and angles with simple explanations and practice activities
What is Trigonometry?
Trigonometry is a branch of mathematics that studies the relationships between the sides and angles of triangles. The word "trigonometry" comes from Greek words meaning "triangle measurement."
We use trigonometry to solve problems involving triangles, especially right-angled triangles (triangles with one 90-degree angle). It helps us find unknown side lengths or angles when we know some measurements.
Trigonometry is used in many real-world situations like architecture, engineering, navigation, and even video game design! It helps us understand how things fit together in space.
Key Concept
Trigonometry helps us solve triangle problems using ratios between sides and angles.
Understanding Right Triangles
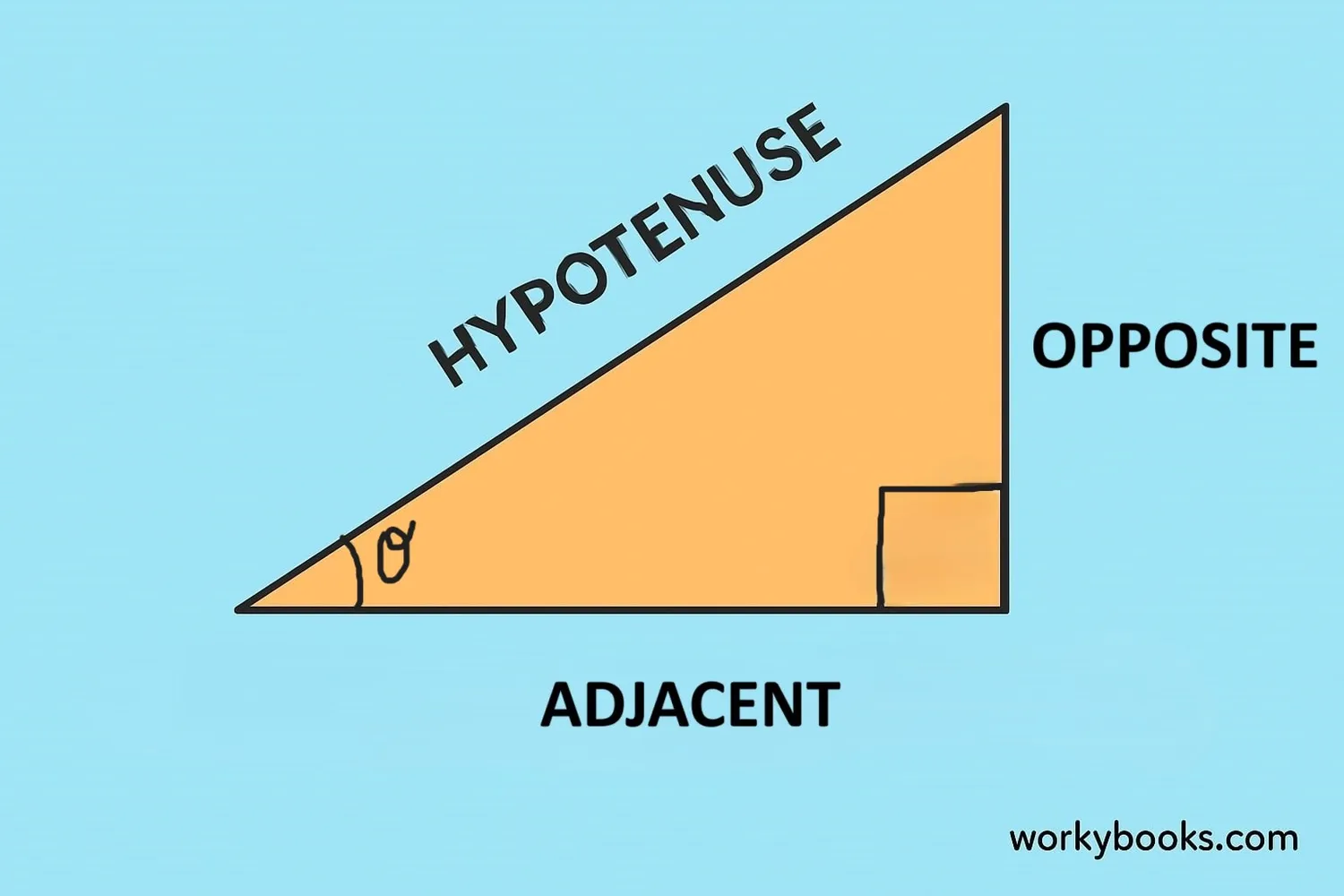
A right triangle has one angle that is exactly 90 degrees. The side opposite the right angle is the longest side and is called the hypotenuse.
The other two sides are called:
- Adjacent - The side next to the angle we're looking at
- Opposite - The side across from the angle we're looking at
Remember
In a right triangle, the hypotenuse is always the longest side and opposite the right angle.
Trigonometric Ratios
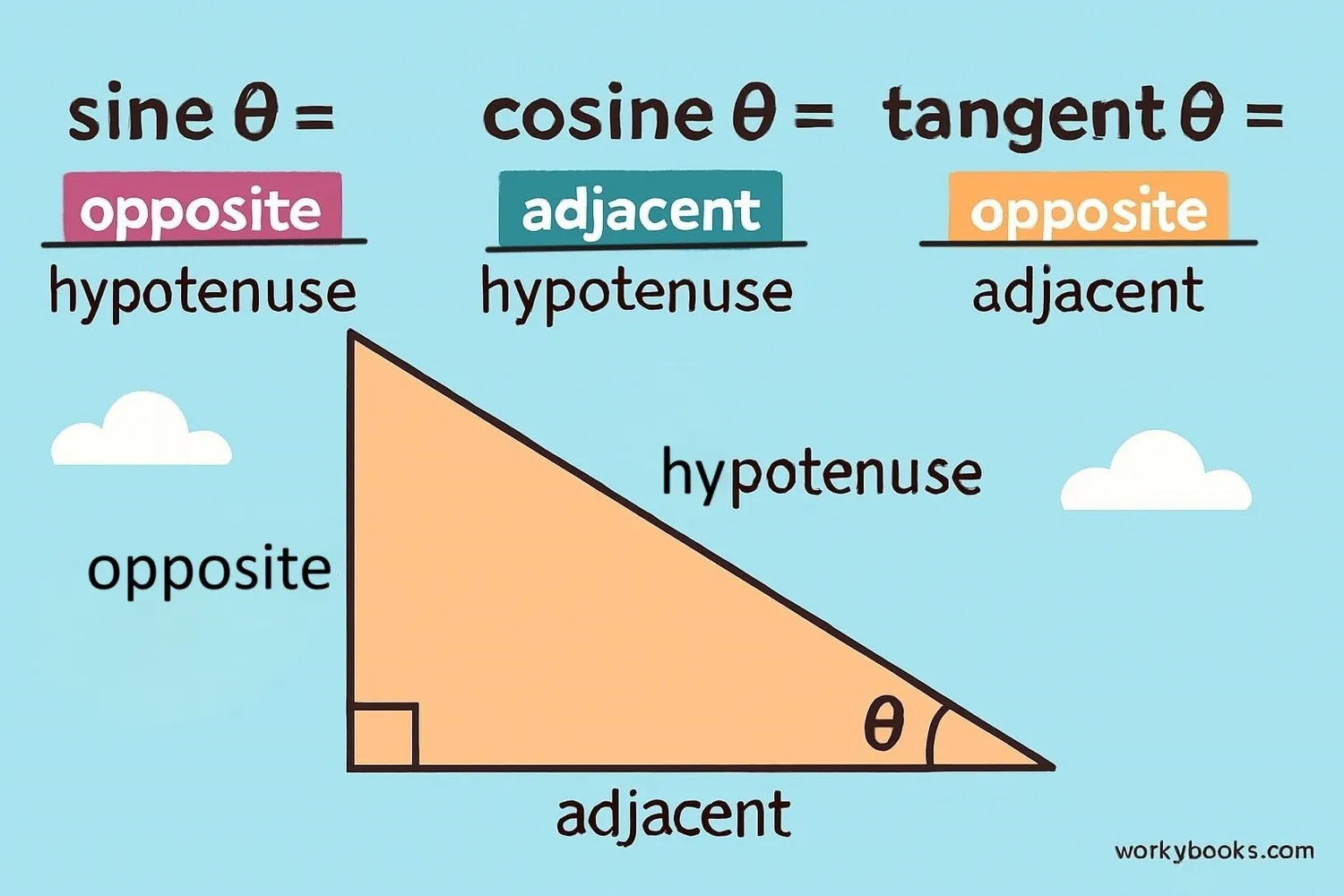
The three basic trigonometric ratios are sine (sin), cosine (cos), and tangent (tan). These are relationships between the sides of a right triangle:
Sine (sin)
Opposite ÷ Hypotenuse
Cosine (cos)
Adjacent ÷ Hypotenuse
Tangent (tan)
Opposite ÷ Adjacent
Remember these with the phrase: SOH-CAH-TOA
- SOH: Sine = Opposite ÷ Hypotenuse
- CAH: Cosine = Adjacent ÷ Hypotenuse
- TOA: Tangent = Opposite ÷ Adjacent
Pythagorean Theorem
The Pythagorean Theorem is a fundamental relationship in right triangles discovered by the ancient Greek mathematician Pythagoras. It states:
Pythagorean Theorem
Where a and b are the legs of the triangle, and c is the hypotenuse
We can use this theorem to find any side of a right triangle when we know the other two sides.
Example: If a right triangle has legs of 3 units and 4 units, what is the hypotenuse?
Solution: 3² + 4² = 9 + 16 = 25. The square root of 25 is 5. So the hypotenuse is 5 units.
Remember
The Pythagorean Theorem only works for right triangles!
Real-World Examples

Let's see how trigonometry helps solve real problems:
Example 1: Finding the height of a tree
If you stand 10 meters from a tree and measure the angle to the top as 40 degrees, how tall is the tree?
Solution: We use tangent: tan(40°) = height / 10 → height = 10 × tan(40°) ≈ 10 × 0.839 ≈ 8.39 meters
Example 2: Calculating a ramp's length
A ramp needs to rise 1 meter over a horizontal distance of 5 meters. How long is the ramp?
Solution: Use the Pythagorean theorem: ramp² = 1² + 5² = 1 + 25 = 26 → ramp = √26 ≈ 5.1 meters
Example 3: Navigation at sea
A ship sails 5 km east and then 12 km north. How far is it from its starting point?
Solution: This forms a right triangle: distance² = 5² + 12² = 25 + 144 = 169 → distance = √169 = 13 km
Application Tip
Trigonometry helps us measure things we can't reach directly - like the height of mountains or distance to stars!
Trigonometry Practice Quiz
Test your trigonometry knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about trigonometry:
Math Trivia
Discover interesting facts about trigonometry and mathematics:
Ancient Origins
Trigonometry dates back to ancient Egypt and Babylon over 4000 years ago! The ancient Egyptians used primitive trigonometry to build the pyramids with remarkable precision.
Hipparchus - The Father
The Greek mathematician Hipparchus (190-120 BC) is considered the founder of trigonometry. He created the first trigonometric table to solve problems in astronomy.
Space Exploration
NASA uses trigonometry to calculate spacecraft trajectories. The Apollo missions to the moon relied on trigonometric calculations for navigation and landing.
Real-World Measurement
In 1852, the Great Trigonometric Survey of India used trigonometry to measure the height of Mount Everest, determining it to be exactly 29,000 feet at first (later adjusted to 29,029 feet).




