Symmetry - Definition, Examples, Quiz, FAQ, Trivia
Learn about different types of symmetry with easy explanations, examples, and activities
What is Symmetry?

Symmetry is when one shape becomes exactly like another when you move it in some way: turn, flip, or slide. Think of it like a mirror image - if you draw a line down the middle of a shape, both sides match perfectly.
Symmetry is all around us! You can find it in nature (like butterfly wings), in art, in buildings, and even in letters of the alphabet. When something is symmetrical, it looks balanced and pleasing to the eye.
There are different types of symmetry, but they all share the idea that parts of a shape match other parts in size, shape, and position.
Key Concept
Symmetry means that one part of a shape is a mirror image of another part when divided along a line, or that a shape looks the same after being rotated or moved.
Line of Symmetry
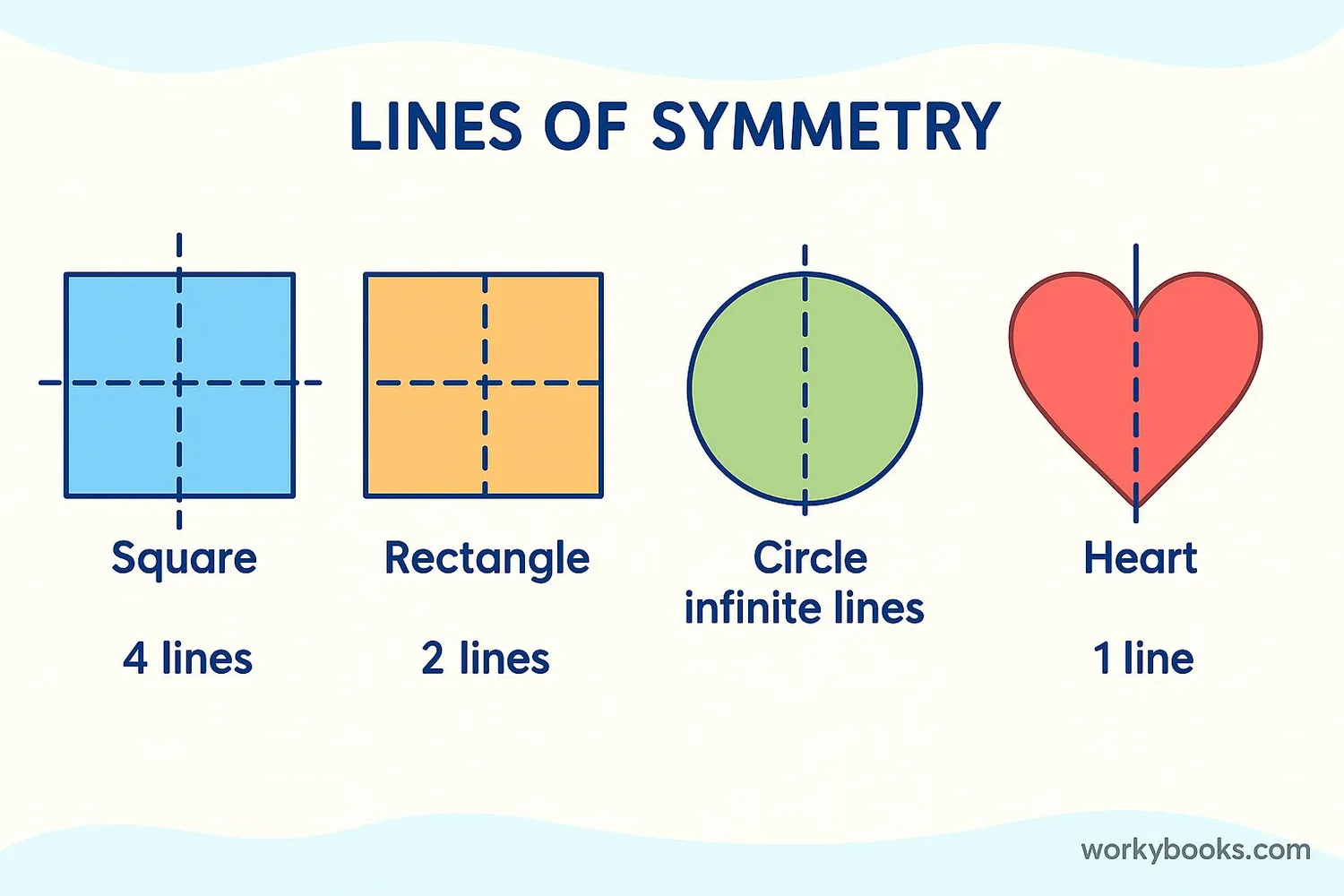
A line of symmetry (also called a mirror line) is a line where you can fold a shape so that both halves match exactly. It's like folding paper in half and both sides are identical.
Different shapes have different numbers of lines of symmetry:
To find lines of symmetry, imagine folding the shape. If both sides match perfectly when folded along a line, that line is a line of symmetry. Some shapes like circles have many lines of symmetry, while others like a scalene triangle have none.
Remember
A shape can have zero, one, or many lines of symmetry. The more symmetrical a shape is, the more lines of symmetry it will have.
Types of Symmetry
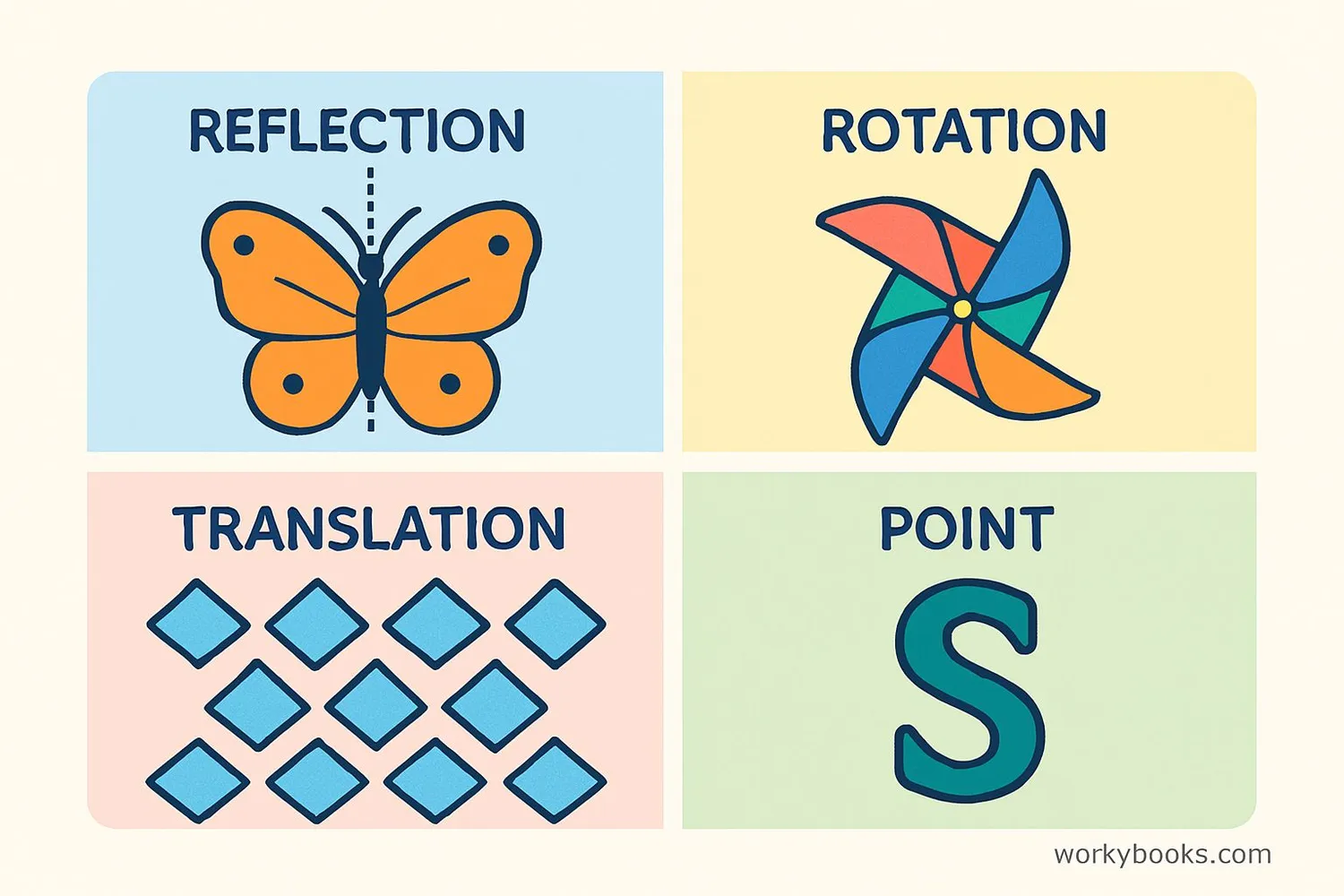
There are several types of symmetry in mathematics. Let's explore the most common ones:
Reflection Symmetry
Also called mirror symmetry, this is the most common type. A shape has reflection symmetry if it can be divided by a line into two identical mirror-image halves. Examples include butterflies, human faces, and capital letters like A, M, T.
Rotational Symmetry
A shape has rotational symmetry when it looks the same after being rotated part of a full turn around its center. The order of rotational symmetry is how many positions the shape matches itself during a full 360° rotation. A square has rotational symmetry of order 4.
Translational Symmetry
This occurs when a pattern can be shifted (translated) along a straight line and still look the same. Think of repeating patterns like tiles on a floor, stripes on a shirt, or waves on water. The pattern repeats at regular intervals.
Point Symmetry
A shape has point symmetry if it looks exactly the same when rotated 180° around a central point. This is sometimes called rotational symmetry of order 2. Examples include the letters S, Z, N, and the symbol +.
Remember
Reflection symmetry is about mirror images, rotational symmetry is about turning, translational symmetry is about sliding, and point symmetry is about half-turns around a center point.
Symmetry Examples
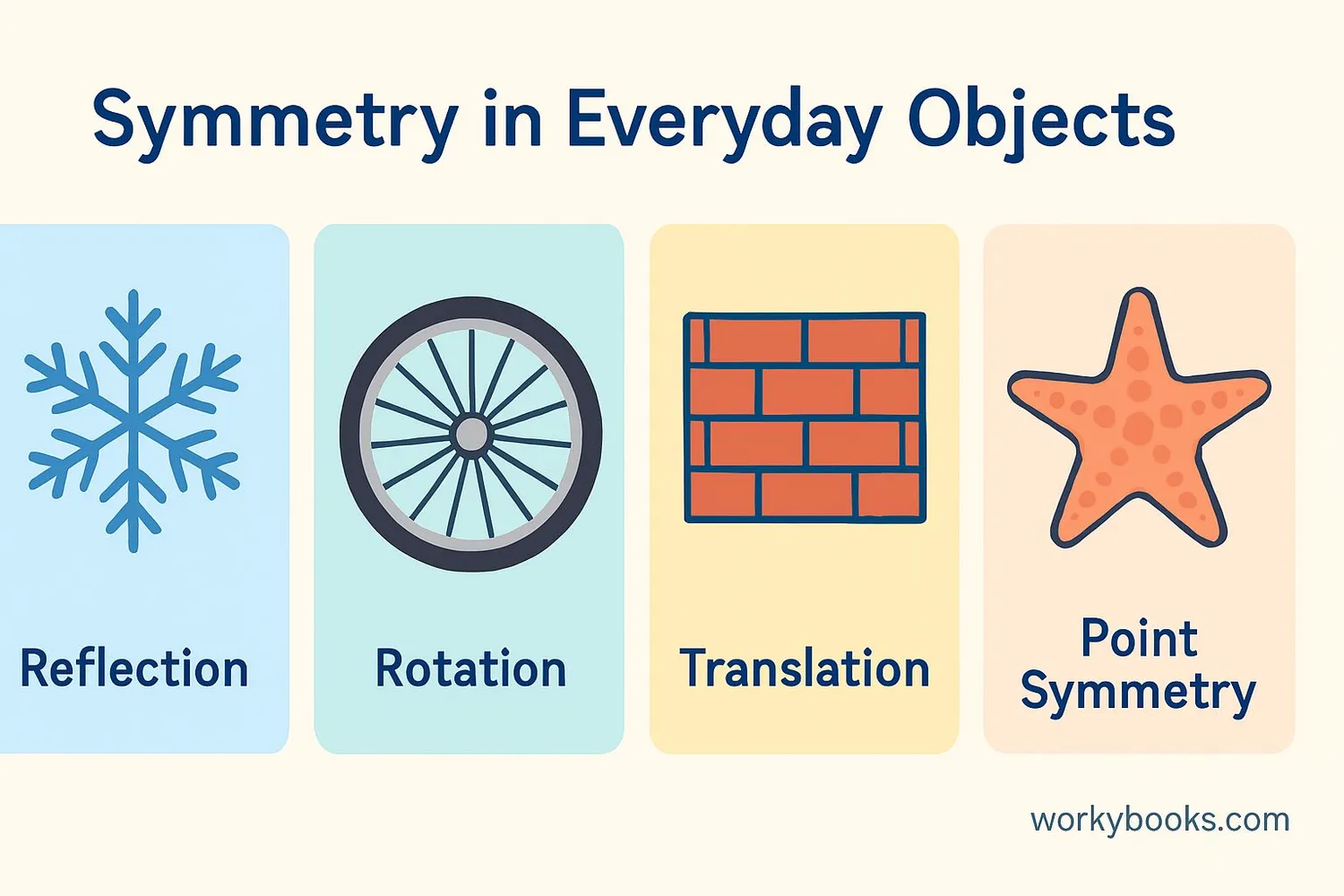
Symmetry is all around us! Here are some examples from everyday life:
Nature
Snowflakes have 6 lines of reflection symmetry. Flowers often have rotational symmetry. Starfish have point symmetry. Butterfly wings are a classic example of reflection symmetry.
Architecture
Many buildings use symmetry to create balance and beauty. The Taj Mahal is famous for its perfect reflection symmetry. Windows, doors, and facades are often symmetrical.
Art & Design
Artists use symmetry to create pleasing compositions. Mandalas show rotational symmetry. Patterns in textiles and wallpaper often use translational symmetry.
Letters & Numbers
Many capital letters have reflection symmetry: A (vertical), B (horizontal), H (both). Numbers like 0 and 8 have both vertical and horizontal symmetry. The letter O has rotational symmetry.
Try This
Look around you right now - how many symmetrical objects can you find? Your notebook, your desk, a window, maybe even your face has approximate symmetry!
Symmetry Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about symmetry:
Symmetry Trivia
Discover fascinating facts about symmetry:
Nature's Symmetry
Honeycombs made by bees show perfect hexagonal symmetry. This shape allows bees to store the most honey using the least amount of wax. Hexagons fit together with no wasted space!
Crystal Symmetry
Snowflakes always have 6 lines of symmetry because of the hexagonal structure of water molecules when they freeze. No two snowflakes are exactly alike, but they all have 6-fold symmetry!
Taj Mahal
The Taj Mahal in India is one of the most symmetrical buildings in the world. Its reflection in the water creates a perfect mirror image, and the entire complex is designed with precise symmetry.
Infinite Symmetry
A circle has an infinite number of lines of symmetry and rotational symmetry at every angle. This makes it the most symmetrical 2D shape possible. Spheres have similar symmetry in 3D space.


