Unit Circle - Definition, Examples, Quiz, FAQ, Trivia
Learn about trigonometric functions with visual explanations and interactive practice
What is the Unit Circle?
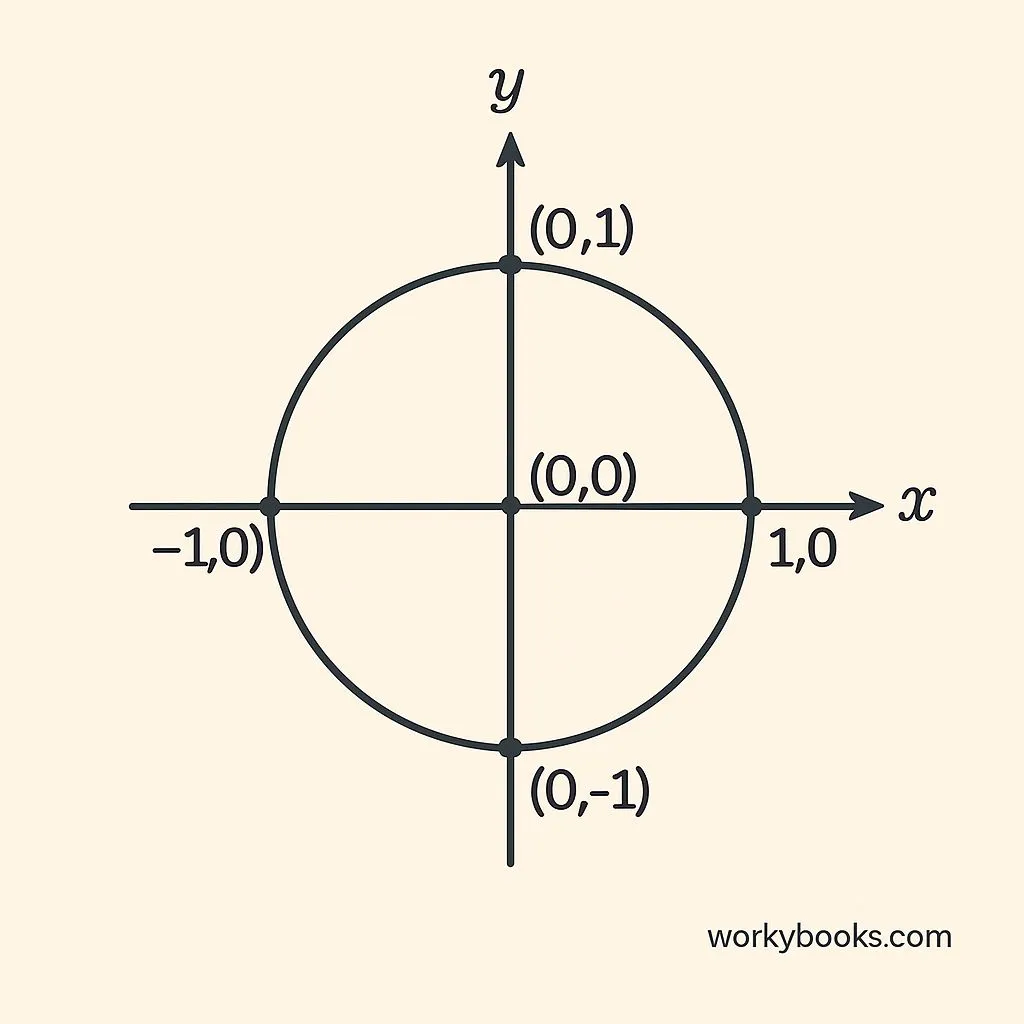
The unit circle is a special circle with a radius of exactly 1 unit. It's centered at the origin point (0,0) on a coordinate plane. This simple circle helps us understand angles and trigonometric functions like sine, cosine, and tangent.
Why is it called "unit"? Because the radius is one unit long. This makes calculations easier because we can use simple fractions instead of complicated numbers.
The unit circle connects geometry with trigonometry. Every point on the circle has coordinates (x, y) that represent cosine and sine values for the angle formed with the positive x-axis.
Key Concept
For any angle θ measured from the positive x-axis, the coordinates of the point on the unit circle are (cos θ, sin θ).
How the Unit Circle Works
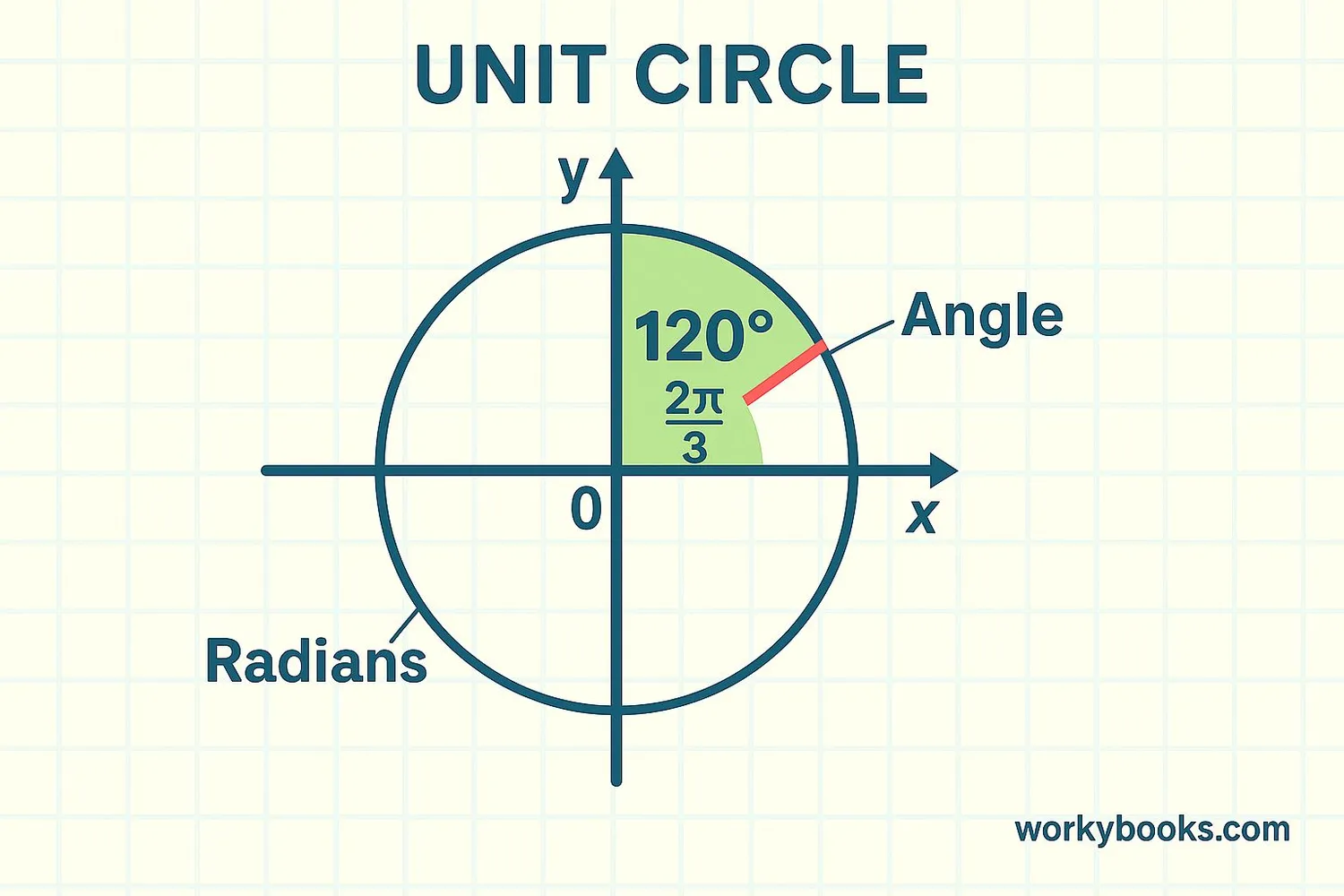
The unit circle uses two ways to measure angles: degrees and radians. Degrees are what you see on a protractor (0° to 360°). Radians are another way to measure angles based on the circle itself.
Key angle measurements:
- 0° (0 radians) - Point at (1, 0)
- 90° (π/2 radians) - Point at (0, 1)
- 180° (π radians) - Point at (-1, 0)
- 270° (3π/2 radians) - Point at (0, -1)
Radians to Degrees
π (pi) is approximately 3.14159 and represents half a circle
Remember
One full circle is 360 degrees or 2π radians. This relationship helps convert between the two measurement systems.
Trigonometric Functions
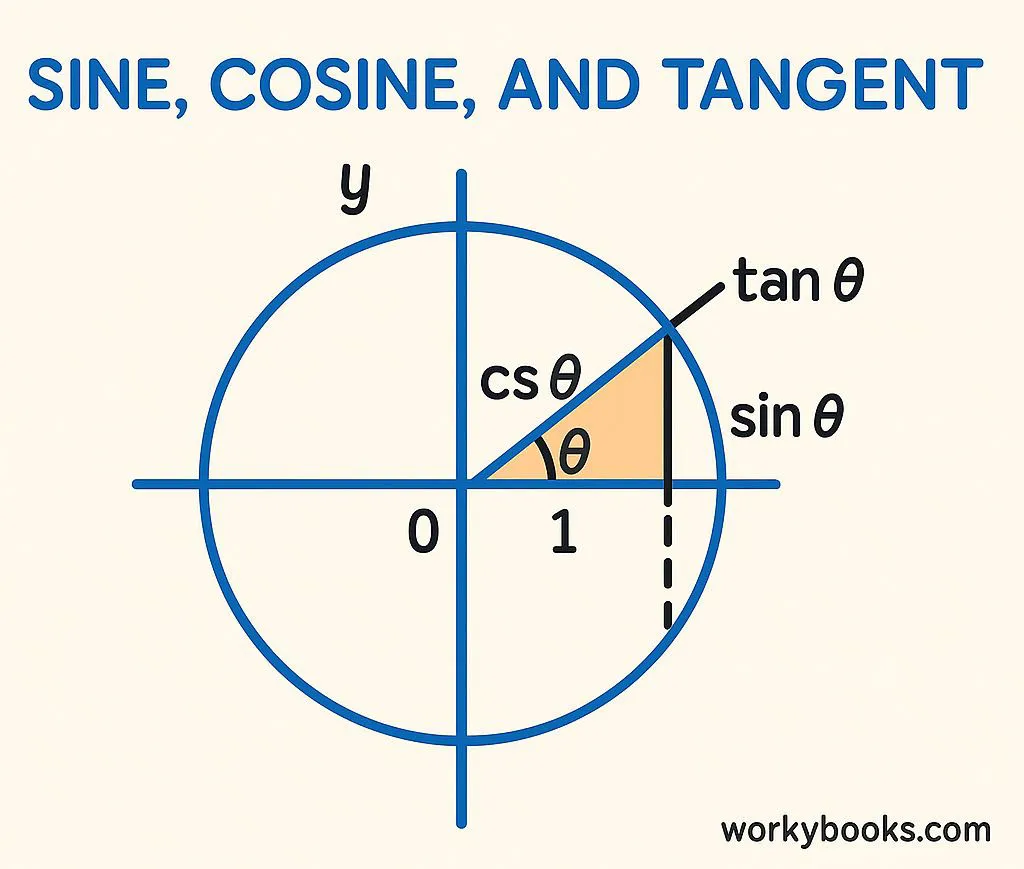
The unit circle helps us define the three main trigonometric functions:
Sine (sin): The y-coordinate of the point on the unit circle
Cosine (cos): The x-coordinate of the point on the unit circle
Tangent (tan): The ratio of sine to cosine (y/x)
These functions help us understand relationships between angles and sides of triangles. The unit circle makes it easy to remember important values:
| Angle (Degrees) | Angle (Radians) | sin | cos | tan |
|---|---|---|---|---|
| 0° | 0 | 0 | 1 | 0 |
| 30° | π/6 | 1/2 | √3/2 | √3/3 |
| 45° | π/4 | √2/2 | √2/2 | 1 |
| 60° | π/3 | √3/2 | 1/2 | √3 |
| 90° | π/2 | 1 | 0 | undefined |
The Pythagorean identity is a special relationship that always holds true on the unit circle:
Unit Circle Chart
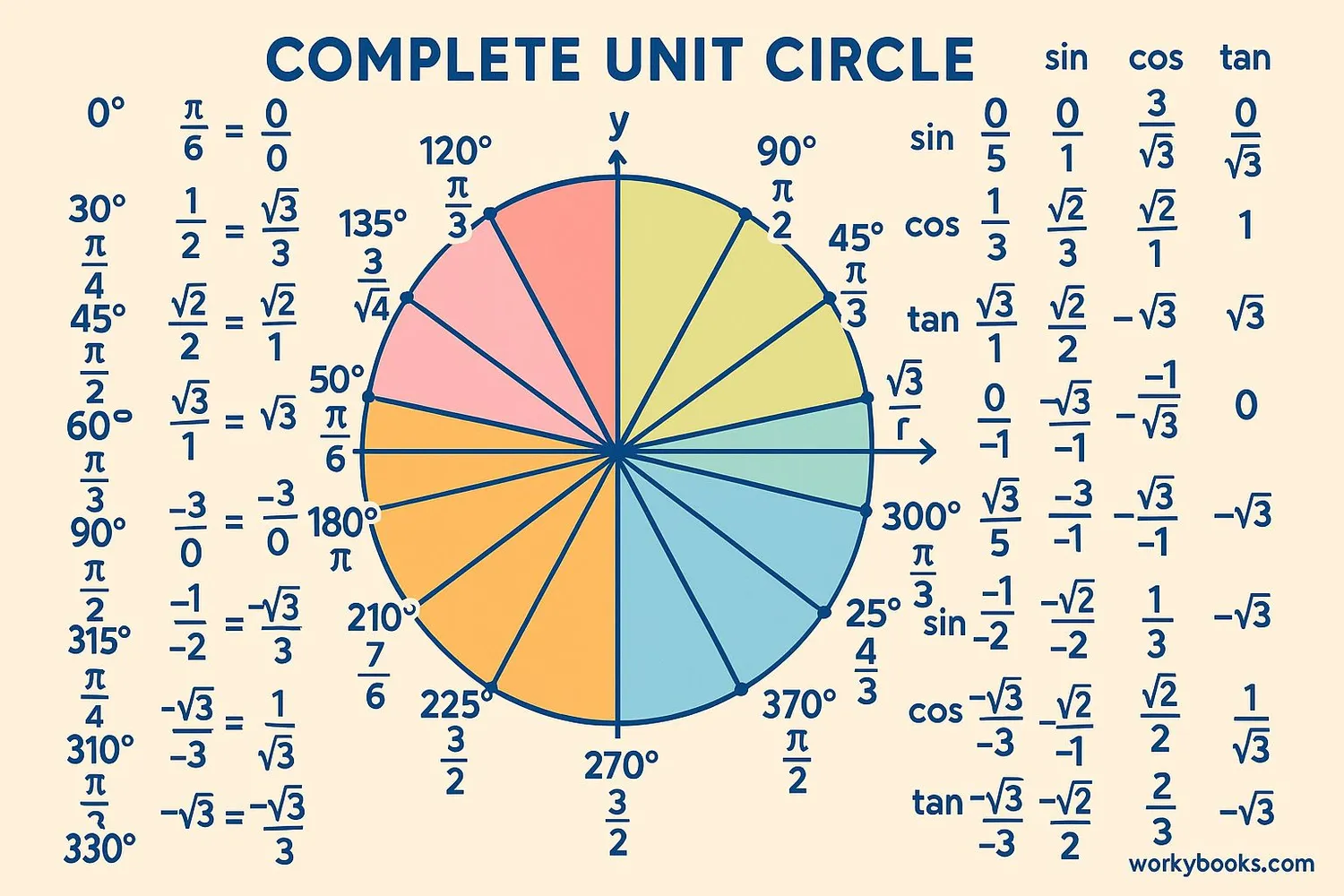
The unit circle chart shows all the important angles and their corresponding sine, cosine, and tangent values. Here's a simplified version:
| Angle | Radians | cos | sin | tan |
|---|---|---|---|---|
| 0° | 0 | 1 | 0 | 0 |
| 30° | π/6 | √3/2 | 1/2 | √3/3 |
| 45° | π/4 | √2/2 | √2/2 | 1 |
| 60° | π/3 | 1/2 | √3/2 | √3 |
| 90° | π/2 | 0 | 1 | ∞ |
| 120° | 2π/3 | -1/2 | √3/2 | -√3 |
| 135° | 3π/4 | -√2/2 | √2/2 | -1 |
| 150° | 5π/6 | -√3/2 | 1/2 | -√3/3 |
| 180° | π | -1 | 0 | 0 |
Notice how the values repeat every 360 degrees (2π radians). This pattern helps us remember the values for all angles.
Chart Tip
The coordinates of each point on the unit circle are always between -1 and 1 because the radius is 1.
Real-World Examples
Let's see how the unit circle helps solve real problems:
Example 1: Find the sine and cosine of 45°
Solution: From the unit circle, at 45° (π/4 radians), both coordinates are √2/2. So sin(45°) = √2/2 and cos(45°) = √2/2.
Example 2: What is the tangent of 60°?
Solution: At 60° (π/3 radians), sin(60°) = √3/2 and cos(60°) = 1/2. Tan = sin/cos = (√3/2) ÷ (1/2) = √3.
Example 3: Verify the Pythagorean identity at 30°
Solution: sin(30°) = 1/2, cos(30°) = √3/2. sin² + cos² = (1/2)² + (√3/2)² = 1/4 + 3/4 = 1. It works!
Example 4: Convert 90° to radians
Solution: Radians = Degrees × (π/180) = 90 × π/180 = π/2.
Conversion Tip
To convert degrees to radians, multiply by π/180. To convert radians to degrees, multiply by 180/π.
Unit Circle Practice Quiz
Test your understanding with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the unit circle:
Math Trivia
Discover interesting facts about trigonometry and circles:
Ancient Origins
Trigonometry dates back to ancient Egyptian and Babylonian mathematicians over 4000 years ago! They used early forms of trigonometry to build pyramids and track stars.
Circle Constant
The number π (pi) has been calculated to over 100 trillion digits, but we only need about 40 digits to calculate the circumference of the observable universe to the width of a hydrogen atom!
Space Navigation
NASA uses trigonometry to navigate spacecraft. The unit circle helps calculate trajectories to the Moon, Mars, and beyond!
Memory Champion
The world record for memorizing digits of π is 70,000 digits! Rajveer Meena recited them for over 10 hours without a mistake.





