X-Intercepts - Definition, Examples, Quiz, FAQ, Trivia
Learn about x-intercepts with visual examples, step-by-step explanations, and practice activities
What is an X-Intercept?
The x-intercept is where a graph crosses the x-axis. At this special point, the y-coordinate is always zero. X-intercepts are important because they show where a function equals zero, which helps us solve equations and understand graphs.
Think of the x-axis as the ground. When a line or curve touches the ground, that's the x-intercept! For example, when you throw a ball, the x-intercept would be where it lands on the ground.
Key things to remember:
- An x-intercept is a point: (x, 0)
- There can be one, many, or no x-intercepts
- X-intercepts are also called "roots" or "zeros"
Key Concept
At the x-intercept, y always equals 0. This is why we set y=0 when solving for x-intercepts.
How to Find X-Intercepts
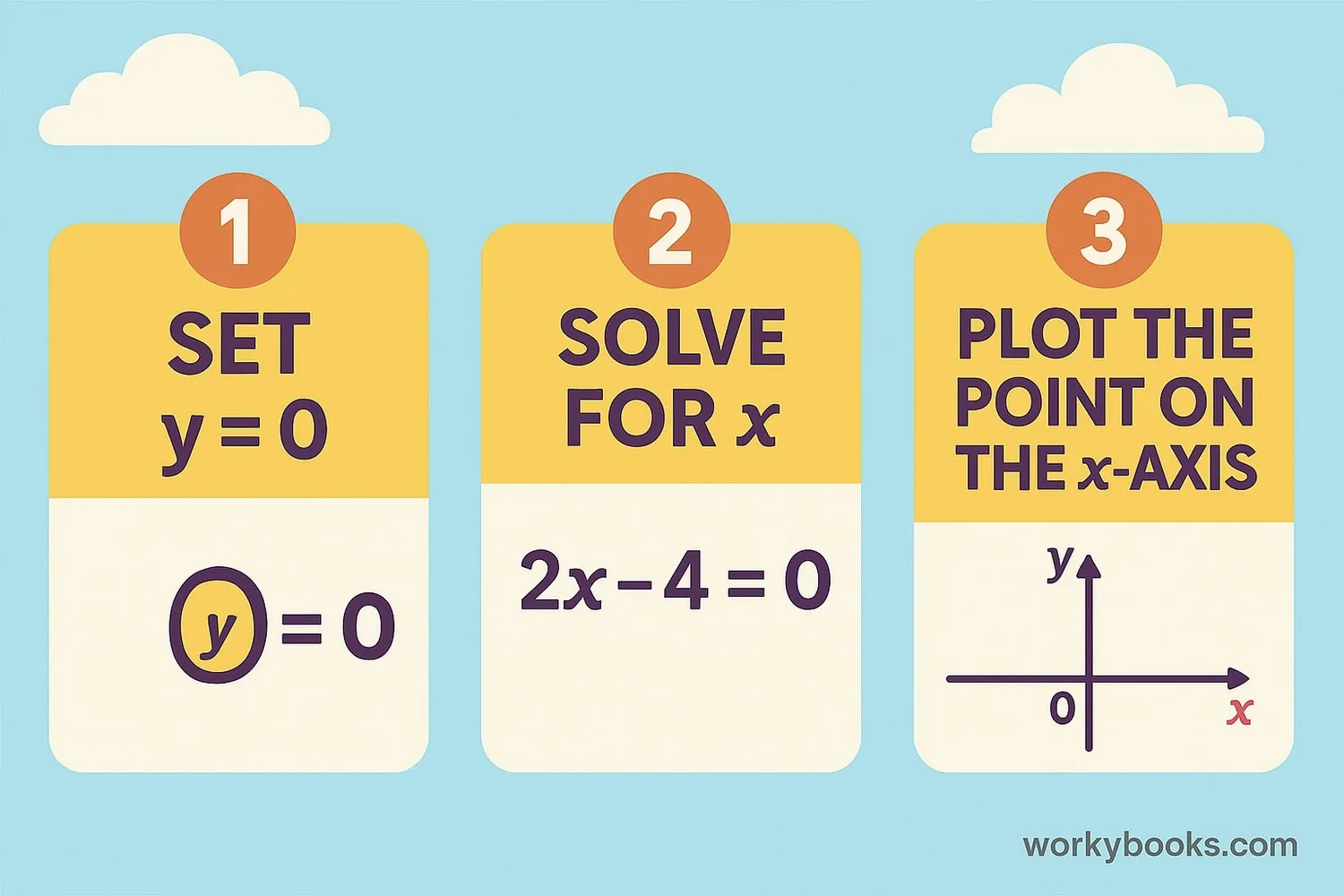
Finding x-intercepts is like solving a mystery! Follow these simple steps:
3 Simple Steps
Let's see how this works with an example:
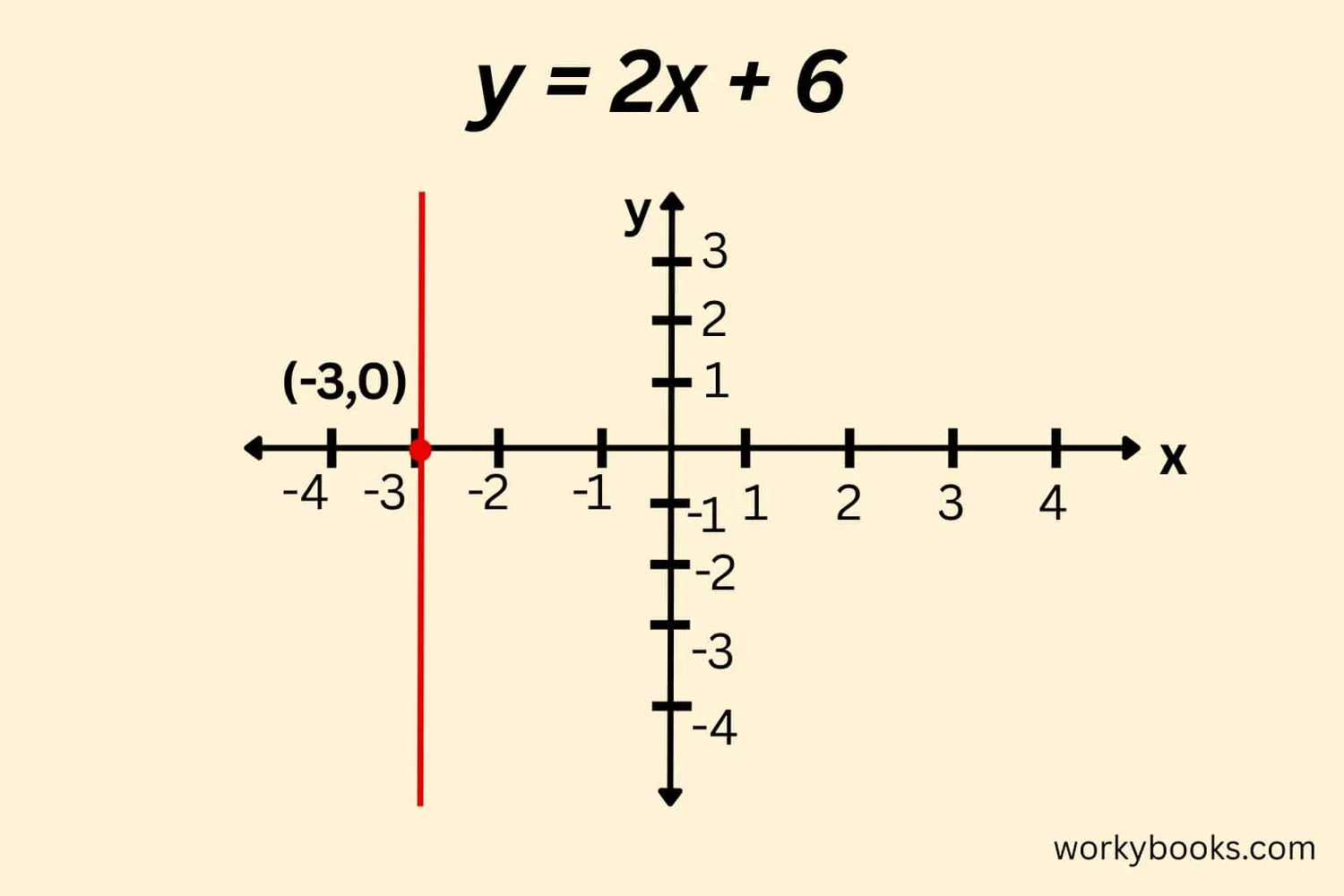
Example: Find the x-intercept of y = 2x + 4
Step 1: Set y = 0 → 0 = 2x + 4
Step 2: Solve for x → 2x = -4 → x = -2
Step 3: The x-intercept is (-2, 0)
That means the line crosses the x-axis at -2 on the x-axis!
Remember
All x-intercepts have a y-value of 0. This is why we set y=0 in the equation.
X-Intercept in Linear Equations
Linear equations make straight lines on a graph. These lines cross the x-axis at exactly one point (unless they're horizontal). The general form is:
Linear Equation Form
Where m is the slope and b is the y-intercept
To find the x-intercept in a linear equation:
1. Set y = 0
2. Solve for x: 0 = mx + b
3. The solution is x = -b/m
Example: Find the x-intercept of y = 3x - 6
0 = 3x - 6 → 3x = 6 → x = 2
The x-intercept is (2, 0)
Pattern
For any linear equation y = mx + b, the x-intercept is at (-b/m, 0).
X-Intercept in Quadratic Equations
Quadratic equations make parabolas (U-shaped curves). These can cross the x-axis at zero, one, or two points. The general form is:
Quadratic Equation Form
To find x-intercepts in quadratic equations:
1. Set y = 0 → 0 = ax² + bx + c
2. Solve the quadratic equation using:
- Factoring: Find two numbers that multiply to ac and add to b
- Quadratic formula: x = [-b ± √(b² - 4ac)] / 2a
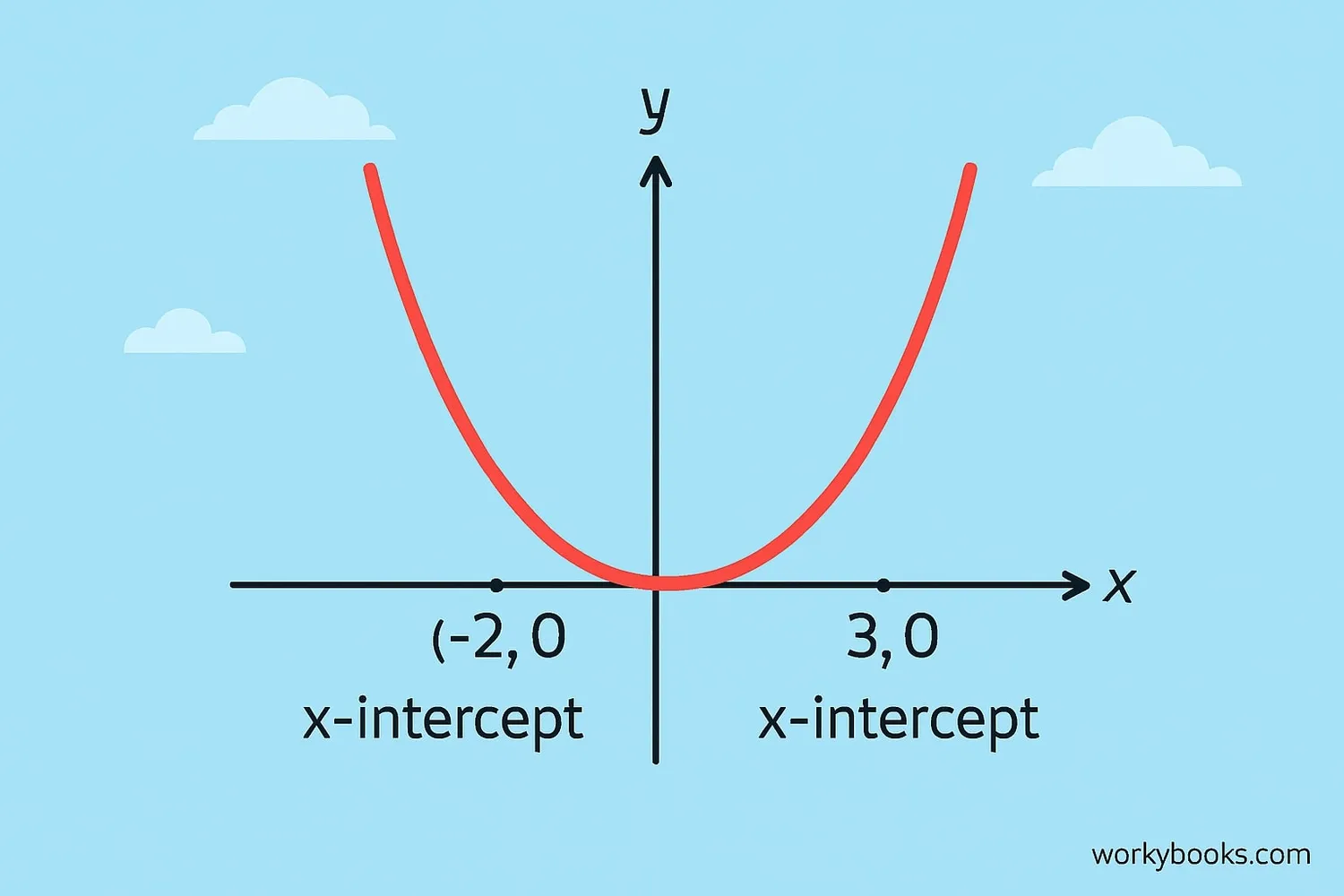
Example: Find the x-intercepts of y = x² - 4
0 = x² - 4 → x² = 4 → x = 2 or x = -2
The x-intercepts are (-2, 0) and (2, 0)
Discriminant
The discriminant (b² - 4ac) tells us how many x-intercepts a quadratic has: positive = 2, zero = 1, negative = 0.
Real-World Examples
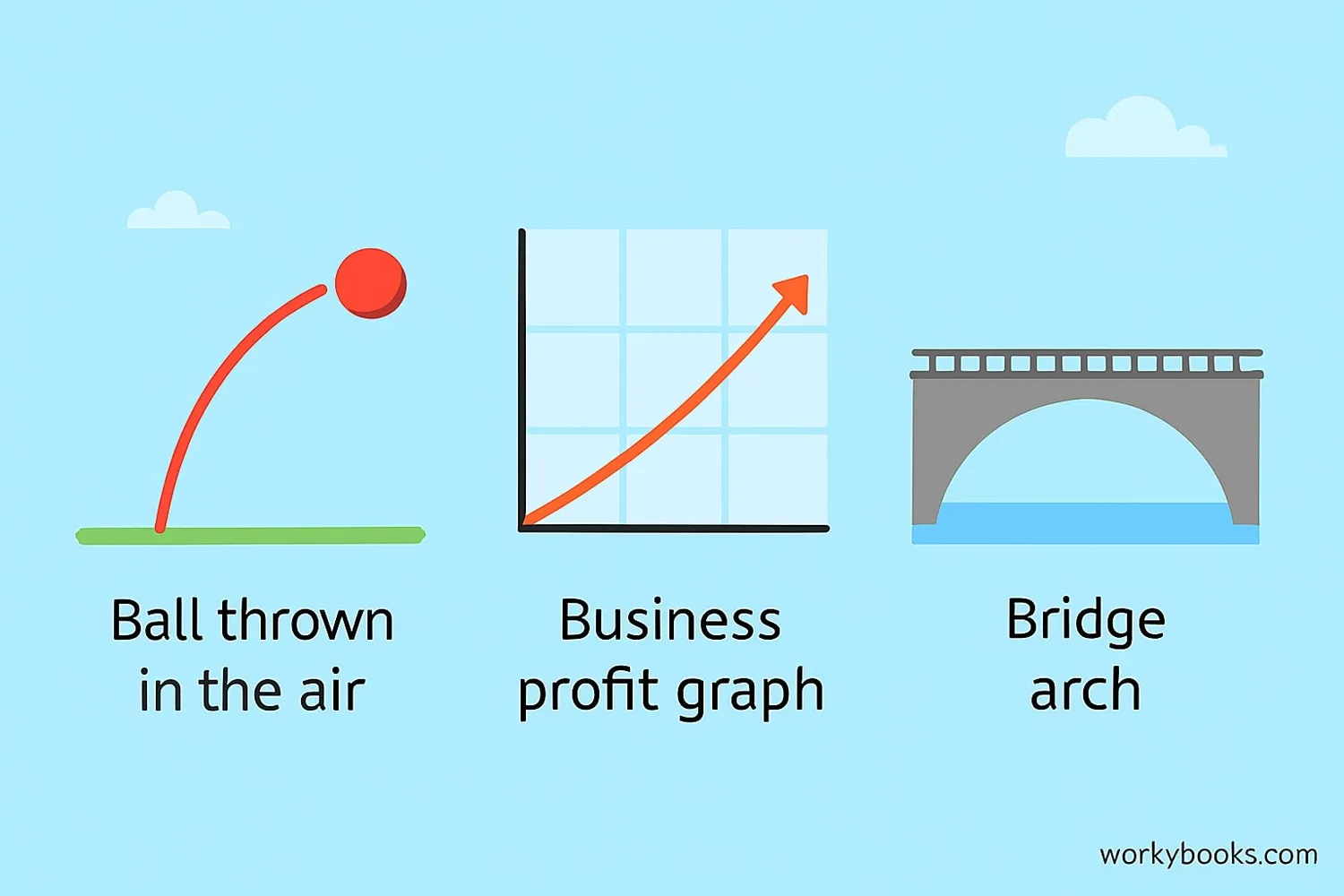
X-intercepts aren't just for math class! They help us solve real problems:
Example 1: Ball Throwing
The height of a ball is h = -5t² + 20t. When does it hit the ground?
Factor: 0 = -5t(t - 4)
t=0 (start) or t=4 (when it hits ground)
Example 2: Business Profit
A company's profit is P = 50x - 1000, where x is items sold. How many items to break even?
50x = 1000 → x = 20
They need to sell 20 items to break even
Example 3: Bridge Design
A bridge arch follows y = -0.1x² + 10. Where does it meet the ground?
0.1x² = 10 → x² = 100 → x = ±10
The arch meets ground at (-10,0) and (10,0)
Real-World Tip
X-intercepts often represent important moments: when something hits ground, breaks even, or crosses a boundary.
X-Intercept Practice Quiz
Test your knowledge with this 5-question quiz. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about x-intercepts:
Math Trivia
Discover interesting facts about graphing and intercepts:
Origin of Coordinate System
The Cartesian coordinate system we use today was invented by French mathematician René Descartes in the 17th century. Legend says he got the idea while watching a fly on his ceiling!
Intercepts in Physics
X-intercepts are used in physics to calculate important moments like when a rocket will hit the ground or when an object will pass through a specific point in space.
NASA Calculations
NASA engineers use x-intercepts to calculate rocket trajectories. The x-intercept of a rocket's path shows where it will land or enter the atmosphere.
Most Intercepts
The polynomial with the most x-intercepts ever practically used has over 100 intercepts! These complex equations help scientists model real-world phenomena like weather patterns.





