Zero Product Property - Definition, Examples, Quiz, FAQ, Trivia
Learn to solve equations using this powerful math rule with easy explanations and practice activities
What is the Zero Product Property?
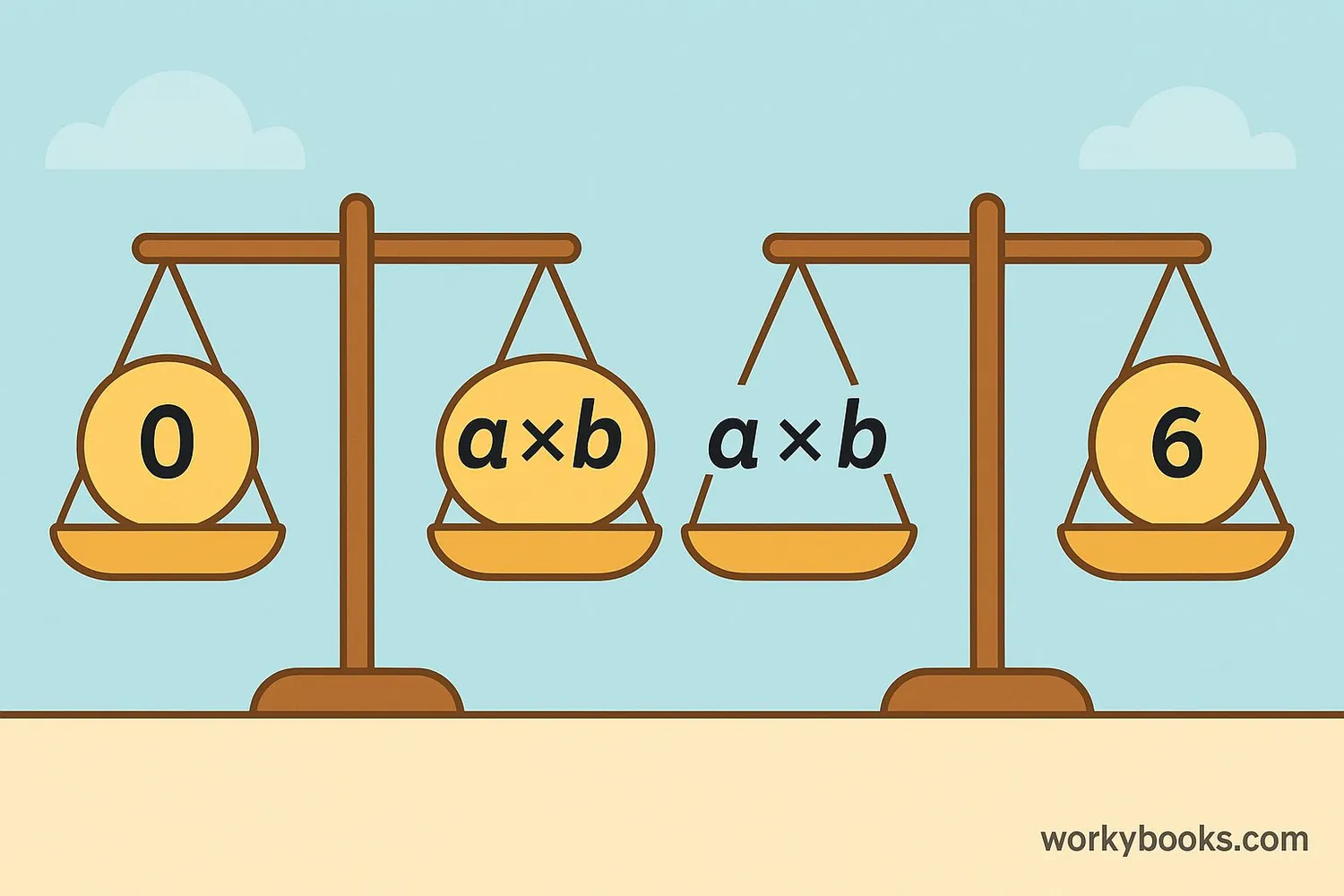
The Zero Product Property is a simple but powerful rule in algebra. It says:
Definition
When two numbers multiply to zero, at least one of them must be zero.
This property helps us solve equations where we have factors multiplied together equaling zero. Instead of solving complicated equations all at once, we can break them into simpler parts.
Key Concept
The Zero Product Property only works when the product is zero. If the product equals any other number, we can't use this property.
How to Use the Zero Product Property
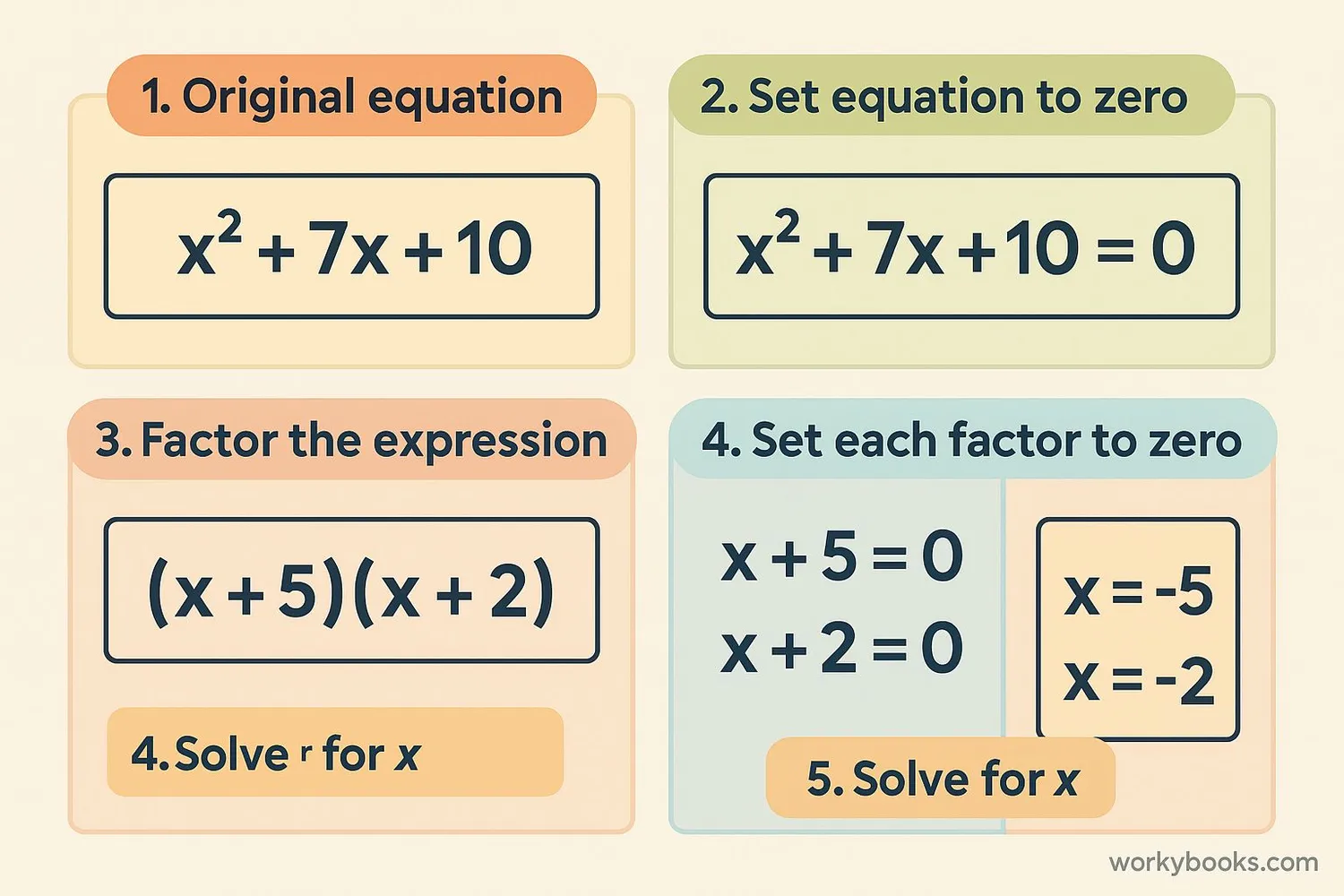
Using the Zero Product Property involves just a few steps. Let's solve an example together:
Solve: (x - 3)(x + 2) = 0
Identify the factors
We have two factors: (x - 3) and (x + 2)
Apply the Zero Product Property
Set each factor equal to zero:
Solve each equation
For x - 3 = 0 → x = 3
For x + 2 = 0 → x = -2
Check your solutions
Plug x = 3: (3-3)(3+2) = (0)(5) = 0 ✓
Plug x = -2: (-2-3)(-2+2) = (-5)(0) = 0 ✓
Remember
Always make sure the equation is set to zero before applying the property. If it's not, rearrange it first!
Why is the Zero Product Property Important?
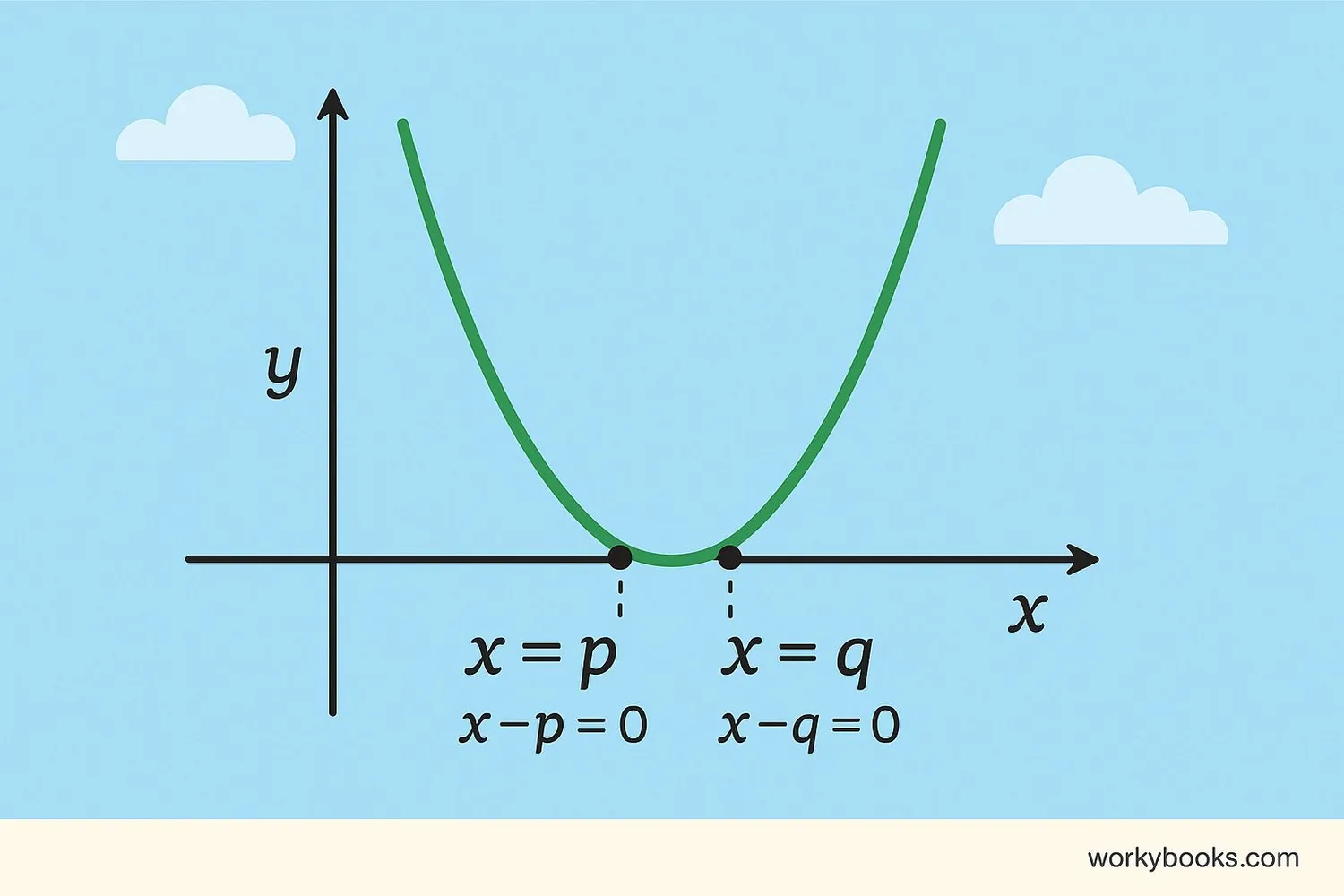
The Zero Product Property is important because:
1. Solving Quadratic Equations: It's the foundation for solving quadratic equations by factoring. Without this property, factoring wouldn't work for finding solutions.
2. Real-World Applications: Engineers use it to solve problems about areas, trajectories, and optimization. For example, finding when a rocket hits the ground or the dimensions that give maximum area.
3. Higher-Level Math: This property extends to polynomials with more factors. For example: If (x-1)(x+2)(x-3)=0, then x=1, x=-2, or x=3.
4. Efficient Problem Solving: It breaks complex problems into simpler parts, making equations easier to solve.
Application Tip
When you see an equation set to zero with multiple factors, the Zero Product Property is your best friend!
Practice Quiz
Test your understanding with these practice questions. Choose the correct answer for each question.
Frequently Asked Questions
Here are answers to common questions about the Zero Product Property:
Math Trivia
Discover interesting facts about algebra and equations:
Ancient Origins
The concept of solving equations dates back to ancient Babylonian mathematicians around 2000 BC. They solved quadratic equations using methods similar to factoring.
Real-World Applications
Engineers use the Zero Product Property to calculate when rockets will return to Earth. By setting the height equation to zero, they find when the rocket hits the ground.
Polynomial Power
The highest degree polynomial equation solved using factoring is the quartic (degree 4). Mathematicians Lodovico Ferrari and Gerolamo Cardano solved it in 1540.
Fundamental Theorem
The Fundamental Theorem of Algebra states that every polynomial equation has at least one solution in complex numbers. This means we can always factor polynomials!





